Difference between revisions of "One-shot games/cs"
(→Obecná definice hry 2 × 2) |
(→Extenzivní hry) |
||
| (55 intermediate revisions by the same user not shown) | |||
| Line 9: | Line 9: | ||
Dobrým příkladem jednorázové hry je konkurzní řízení při likvidaci firmy, kdy všichni zúčastnění se snaží ze zbankrotované firmy dostat co nejvíce peněz. Ovšem v případě, že firma funguje zdravě, hrají akcionáři [[Multistage Games/cs|vícekolovou hru]], jejich strategie bude dlouhodobá a nebudou se snažit z firmy vytáhnout v co nejkratším čase co nejvíce peněz.<ref name="chvoj">CHVOJ, M. <i>Pokročilá teorie her ve světě kolem nás</i> Praha : Grada, 2013, ISBN 978-80-247-4620-3.</ref> | Dobrým příkladem jednorázové hry je konkurzní řízení při likvidaci firmy, kdy všichni zúčastnění se snaží ze zbankrotované firmy dostat co nejvíce peněz. Ovšem v případě, že firma funguje zdravě, hrají akcionáři [[Multistage Games/cs|vícekolovou hru]], jejich strategie bude dlouhodobá a nebudou se snažit z firmy vytáhnout v co nejkratším čase co nejvíce peněz.<ref name="chvoj">CHVOJ, M. <i>Pokročilá teorie her ve světě kolem nás</i> Praha : Grada, 2013, ISBN 978-80-247-4620-3.</ref> | ||
| − | =Jednokolové hry= | + | =Jednokolové hry<ref name="petrzelka">PETRŽELKA, J. <i>Opakované hry s neúplnou informací.</i> Masarykova univerzita: Přírodovědecká fakulta [online]. 2017 [cit. 2020-06-07]. Dostupné z: https://is.muni.cz/th/qc0jx/PetrzilkaDP.pdf</ref>= |
Definice jednokolových her je i základem definic jednotlivých kol, podher u [[Multistage Games/cs|her vícekolových]]. Definice těchto podher budou předmětem následujícíh podkapitol. Pro zjednoduššení se budeme zabývat pouze hrami 2 × 2, dvě strategie. Většina definic bude tedy zjednoduššena právě pouze pro tento typ hry. | Definice jednokolových her je i základem definic jednotlivých kol, podher u [[Multistage Games/cs|her vícekolových]]. Definice těchto podher budou předmětem následujícíh podkapitol. Pro zjednoduššení se budeme zabývat pouze hrami 2 × 2, dvě strategie. Většina definic bude tedy zjednoduššena právě pouze pro tento typ hry. | ||
| − | + | ||
| + | ==Strategické hry 2 × 2== | ||
Definice hry 2 × 2 v obecném tvaru jsou následující: | Definice hry 2 × 2 v obecném tvaru jsou následující: | ||
| − | + | ;Obecná definice hry 2 × 2 | |
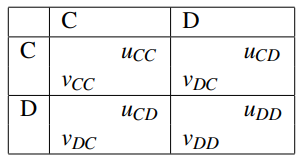
Uspořádaná pětice znaků <math>(2,\{C,D\},\{C,D\},u,v)</math> je hrou v obecném tvaru, kde počet hráčů této hry jsou 2, <math>\{C,D\}</math> je množinou strategií, A je množina strategií hráče prvního a množina B je strategií druhého hráče a <math>u = u(a,b)</math>, <math>v = v(a,b)</math> jsou výplatní funkcí hráčů. <math>a \isin A</math> a <math>b \isin B</math>. Výplatní matice je definována následovně: | Uspořádaná pětice znaků <math>(2,\{C,D\},\{C,D\},u,v)</math> je hrou v obecném tvaru, kde počet hráčů této hry jsou 2, <math>\{C,D\}</math> je množinou strategií, A je množina strategií hráče prvního a množina B je strategií druhého hráče a <math>u = u(a,b)</math>, <math>v = v(a,b)</math> jsou výplatní funkcí hráčů. <math>a \isin A</math> a <math>b \isin B</math>. Výplatní matice je definována následovně: | ||
[[File:vyplatni_matice.png]] | [[File:vyplatni_matice.png]] | ||
| − | Takovýchto her je mnoho, ale značení v definici vychází z nejznámnější z nich a to z [[Prisoner's dilemma/cs|vězňova dilematu]]. Což je hra, kdy hráči můžou buďto <i>spolupracovat</i> (proto C jako cooperate) nebo se zradit jinými slovy <i>bojovat</i> (proto D jako defection). V tomto případě platí nerovnost <math>u_{DC}>u_{DD}>u_{CC}>u_{CD}</math> pro prvního hráče a velmi obodbná i pro hráče druhého. | + | Takovýchto her je mnoho, ale značení v definici vychází z nejznámnější z nich a to z <i>[[Prisoner's dilemma/cs|vězňova dilematu]]</i>. Což je hra, kdy hráči můžou buďto <i>spolupracovat</i> (proto C jako cooperate) nebo se zradit jinými slovy <i>bojovat</i> (proto D jako defection). V tomto případě platí nerovnost <math>u_{DC}>u_{DD}>u_{CC}>u_{CD}</math> pro prvního hráče a velmi obodbná i pro hráče druhého. |
| + | |||
| + | Podobným příkladem může být <i>souboj pohlaví</i>, což je hra ve které oba hráči, kteří chtějí trávit čas společně, ale každý má jinou představu o programu společně stráveného času. Jeden z hráčů chce jít například do <i>kina</i> (strategie C jako cinema) a druhý chce jít na <i>romantickou večeři</i> s (strategie D jako dinner). V tom případě pro prvního hráče platí <math>u_{DD}>u_{CC}>u_{DC} \geq u_{CD}</math> a pro druhého <math>v_{CC}>v_{DD}>v_{CD} \geq v_{DC}</math>. | ||
| + | |||
| + | ;Definice Nashovy rovnováhy | ||
| + | Strategie <math>a^*,b^*</math> je Nashovou rovnováho v případě, že pro všechny ostatní strategie pro oba hráče platí <math>u(a^*,b^*) \geq u(a,b^*)</math> a <math>v(a^*,b^*) \geq u(a^*,b)</math> pro všechny <math>a \ne a^*</math> a <math>b \ne b^*</math>. | ||
| + | Jsou to dvojice strategií, kdy se ani jednomu z hráčů nevyplatí vyjít vstříc druhému hráči. Hledání těchto strategií je také předmětem [[Repeated games/cs|opakovaných her]]. | ||
| + | V klasickém případě [[Prisoner's dilemma/cs|vězňova dilematu]] se ukazuje, že [[Nash equilibrium/cs|Nashova rovnováha]] může být nevýhodná. V této hře je totiž rovnováhou situace, kdy se hráči udávají, ale oba by si polepšili, kdyby se neudali. | ||
| + | |||
| + | ===Smíšené strategie=== | ||
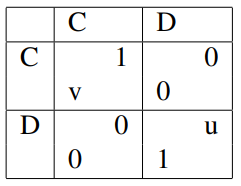
| + | Tuto strategii budeme vysvětlovat na hře s názvem <i>souboj pohlaví</i>. Její matice vypadá následovně: | ||
| + | |||
| + | [[File:matice_souboj_pohlavi.png]] | ||
| + | |||
| + | Použijeme totožný případ, jaký jsme zmiňovali výše a to, že oba hráči, chtějí trávit čas společně, ale každý má jinou představu o programu společně stráveného času. Jeden z hráčů chce jít do <i>kina</i> (strategie C jako cinema) a druhý chce jít na <i>romantickou večeři</i> s (strategie D jako dinner). <math>u</math> a <math>v</math> jsou tedy čísla v intervalu <math>(0,1)</math> a v případě, že zůstanou doma mají oba nulovou výplatu. | ||
| + | V klasických strategiích v této hře existují dvě [[Nash equilibrium/cs|Nashovy rovnováhy]]. Jedna z nich je, že půjdu na večeři (DD) a druhá, že půjdou do kina (CC). | ||
| + | |||
| + | ;Definice smíšené strategie a očekávané výplaty | ||
| + | Smíšená strategie je pravděpodobnostní rozdělení nad množinou čistých strategií <math>A</math> pro prvního a <math>B</math> pro druhého hráče. A je pravděpodobnost <math>p(D)=p</math>, že hráč bude hrát strategii <math>D</math> a <math>q(D)=q</math> jakožto pravděpodobnost, že strategii D bude hrát hráč druhý. V tomto případě je poté <math>u(p,q)=pqu(D,D)+(1-p)(1-q)u(C,C)+p(1-q)u(D,C)+(1-p)qu(C,D)</math> a pro druhého hráče obdobně. | ||
| + | |||
| + | V případě, že hráči hrají strategie popsané výše, je [[Nash equilibrium/cs|Nashova rovnováha]] definována následovně: | ||
| + | |||
| + | ;Definice [[Nash equilibrium/cs|Nashovy rovnováhy]] ve smíšených strategiích | ||
| + | Dvě spíšené strategie <math>p^*,q^*</math> je [[Nash equilibrium/cs|Nashovou rovnováhou]] v případě, pokud pro všechny ostatní smíšené strategie pro oba hráče platí <math>u(p^*,q^*) \geq u(p,q^*)</math> a <math>v(p^*,q^*) \geq u(p^*,q)</math> pro všechny <math>p\ne p^* a q\ne q^*</math>.<ref name="manas">MAŇAS, M. <i>Teorie her a její aplikace.</i> Praha : SNTL, 1991, ISBN 80-03-00358-X.</ref> | ||
| + | |||
| + | ==Extenzivní hry== | ||
| + | Mezistupněm mezi strategickými a [[Repeated games/cs|opakovanými hrami]] jsou hry extenzivní. Přesněji řešeno jsou [[Repeated games/cs|opakované hry]] speciálním případem extenzivních her. | ||
| + | Extenzivní hry jsou hry, které se hrají na kola. Příkladem můžou být třeba šachy, ve kterých v každém kole hraje pouze jeden z hráčů. | ||
| + | |||
| + | ;Definice extenzivní hry | ||
| + | Extenzivní hrou rozumíme uspořádnou čtveřici <math>(N,H,P,u_i)</math>, kde je množina hráčů je <math>N</math>.<math>H</math> je množina posloupností, které splňují tři podmínky a to, že <math>\epsilon \isin H</math>, kde <math>\epsilon</math> je prázdná množina. Další podmínkou je, že <math>(a^k)_{k=1,...,K} \epsilon H \Rightarrow \forall L<K : (a^k)_{k=1,...,L} \epsilon H </math> a v případě, že nekonečná řada <math>(a^k)^\infty_{k=1}</math> skládá z řad takových, že <math>(a^k)_{k=1,...,L} \epsilon H</math> pro všechna <math>L</math> potom i <math>(a^k)^\infty_{k=1} \epsilon H</math>. Takovou množinu nazýváme množinou historíí a její prvny historie, budeme značit <math>h</math>.<math>K</math> bude potom nejvyšší <math>L</math> pro něž platí <math>h \epsilon H</math>. Toto číslo budeme nazývat počtem kol. <math>P(h)</math> je funkce hrajících hráčů, kde <math>h</math> je již známá historie(v případě, že jsme v kole <math>L</math>, potom platí <math>h=(a^k)_{k=1,...,L-1}</math>. Tedy obor hodnot <math>H_P(h) = \{N,k\}</math>, kde <math>k</math> značí konec hry. Historie, pro které platí <math>P(h)=k</math> budeme nazývat konečné, jejich množinu budeme značit <math>Z</math> a jednotlivé strategie <math>z,z \epsilon Z</math>. <math>u_i(z),i \epsilon N</math> je výplatní funkce hráče <math>i</math> na množině konečných historií. Podle této definice máme hru, která se hraje v <math>K</math> kolech a v každém kole hraje konkrétní počet hráčů. V každém dalším kole hráčihrají podle toho, co se už odehrálo. Příkladem může být vstup konkurence na monopolní trh. | ||
| + | |||
| + | ;Definice profilu strategií | ||
| + | Profilem stragií v extenzivní hře <math>(N,H,P,u_i)</math> hráče <math>i \epsilon N</math> je funkce <math>A_i(h)</math>. Definiční obor této funkce je <math>D_{A_i}(h)=\{h \epsilon H:P(h)=i\}</math>. Výstup hry se potom rozumí funkce <math>O(A_1,...,A_n) = z,z \epsilon Z</math>. | ||
| + | |||
| + | ;Definice [[Nash equilibrium/cs|Nashovy rovnováhy]] v sekvenční hře | ||
| + | Nashhovou rovnováhou v sekvenční hře <math>(N,H,P,u_i)</math> se rozumí profil strategií <math>A^*</math> takový, že pro každého hráče <math>i \epsilon N</math> platí <math>u(O_i(A^*))\geq u(O(A^*_i,A_i))</math>, kde <math>A^*_i,A_i</math> znamená, že všichni kromě i-tého hráče hrajou danou strategii.<ref name="friedman">FRIEDMAN, J.W. <i>Game Theory with Applications to Economics. (Second edition).</i> New York : Oxford University Press, 1991, ISBN 0-19-506355-4.</ref> | ||
=Odkazy= | =Odkazy= | ||
<references/> | <references/> | ||
Latest revision as of 20:31, 8 June 2020
Contents
Úvod
Pod pojmem jednorázové (jednokolové) hry se v Teorii her rozumí hrám, ve kterých hráči odehrají pouze jednu hru, na jejímž konci si rozdělí výplaty a zkušenosti nabyté během hry už dále neuplatňují. Žádná další kola nenásledují a tudíž podle toho i hráč volí svojí strategii. Naproti tomu ve vícekolových hrách se hraje hra vícekrát za sebou a tak hráči před každým kolem mohou měnit strategie.
Je potřeba také zmínit, že v případě, že hráči hrají poslední kolo vícekolové hry, chovají se, jako kdyby hráli jednorázovou hru. Z toho vyplývá, že volba strategie se mění na základě počtu kol, která mají hráči před sebou.
Dobrým příkladem jednorázové hry je konkurzní řízení při likvidaci firmy, kdy všichni zúčastnění se snaží ze zbankrotované firmy dostat co nejvíce peněz. Ovšem v případě, že firma funguje zdravě, hrají akcionáři vícekolovou hru, jejich strategie bude dlouhodobá a nebudou se snažit z firmy vytáhnout v co nejkratším čase co nejvíce peněz.[1]
Jednokolové hry[2]
Definice jednokolových her je i základem definic jednotlivých kol, podher u her vícekolových. Definice těchto podher budou předmětem následujícíh podkapitol. Pro zjednoduššení se budeme zabývat pouze hrami 2 × 2, dvě strategie. Většina definic bude tedy zjednoduššena právě pouze pro tento typ hry.
Strategické hry 2 × 2
Definice hry 2 × 2 v obecném tvaru jsou následující:
- Obecná definice hry 2 × 2
Uspořádaná pětice znaků Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (2,\{C,D\},\{C,D\},u,v)} je hrou v obecném tvaru, kde počet hráčů této hry jsou 2, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \{C,D\}} je množinou strategií, A je množina strategií hráče prvního a množina B je strategií druhého hráče a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u = u(a,b)} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v = v(a,b)} jsou výplatní funkcí hráčů. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a \isin A} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b \isin B} . Výplatní matice je definována následovně:
Takovýchto her je mnoho, ale značení v definici vychází z nejznámnější z nich a to z vězňova dilematu. Což je hra, kdy hráči můžou buďto spolupracovat (proto C jako cooperate) nebo se zradit jinými slovy bojovat (proto D jako defection). V tomto případě platí nerovnost Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u_{DC}>u_{DD}>u_{CC}>u_{CD}} pro prvního hráče a velmi obodbná i pro hráče druhého.
Podobným příkladem může být souboj pohlaví, což je hra ve které oba hráči, kteří chtějí trávit čas společně, ale každý má jinou představu o programu společně stráveného času. Jeden z hráčů chce jít například do kina (strategie C jako cinema) a druhý chce jít na romantickou večeři s (strategie D jako dinner). V tom případě pro prvního hráče platí Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u_{DD}>u_{CC}>u_{DC} \geq u_{CD}} a pro druhého Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v_{CC}>v_{DD}>v_{CD} \geq v_{DC}} .
- Definice Nashovy rovnováhy
Strategie Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a^*,b^*} je Nashovou rovnováho v případě, že pro všechny ostatní strategie pro oba hráče platí Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u(a^*,b^*) \geq u(a,b^*)} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(a^*,b^*) \geq u(a^*,b)} pro všechny Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a \ne a^*} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b \ne b^*} . Jsou to dvojice strategií, kdy se ani jednomu z hráčů nevyplatí vyjít vstříc druhému hráči. Hledání těchto strategií je také předmětem opakovaných her. V klasickém případě vězňova dilematu se ukazuje, že Nashova rovnováha může být nevýhodná. V této hře je totiž rovnováhou situace, kdy se hráči udávají, ale oba by si polepšili, kdyby se neudali.
Smíšené strategie
Tuto strategii budeme vysvětlovat na hře s názvem souboj pohlaví. Její matice vypadá následovně:
Použijeme totožný případ, jaký jsme zmiňovali výše a to, že oba hráči, chtějí trávit čas společně, ale každý má jinou představu o programu společně stráveného času. Jeden z hráčů chce jít do kina (strategie C jako cinema) a druhý chce jít na romantickou večeři s (strategie D jako dinner). Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v} jsou tedy čísla v intervalu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (0,1)} a v případě, že zůstanou doma mají oba nulovou výplatu. V klasických strategiích v této hře existují dvě Nashovy rovnováhy. Jedna z nich je, že půjdu na večeři (DD) a druhá, že půjdou do kina (CC).
- Definice smíšené strategie a očekávané výplaty
Smíšená strategie je pravděpodobnostní rozdělení nad množinou čistých strategií Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A} pro prvního a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle B} pro druhého hráče. A je pravděpodobnost Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p(D)=p} , že hráč bude hrát strategii Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle D} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q(D)=q} jakožto pravděpodobnost, že strategii D bude hrát hráč druhý. V tomto případě je poté Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u(p,q)=pqu(D,D)+(1-p)(1-q)u(C,C)+p(1-q)u(D,C)+(1-p)qu(C,D)} a pro druhého hráče obdobně.
V případě, že hráči hrají strategie popsané výše, je Nashova rovnováha definována následovně:
- Definice Nashovy rovnováhy ve smíšených strategiích
Dvě spíšené strategie Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p^*,q^*} je Nashovou rovnováhou v případě, pokud pro všechny ostatní smíšené strategie pro oba hráče platí Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u(p^*,q^*) \geq u(p,q^*)} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle v(p^*,q^*) \geq u(p^*,q)} pro všechny Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p\ne p^* a q\ne q^*} .[3]
Extenzivní hry
Mezistupněm mezi strategickými a opakovanými hrami jsou hry extenzivní. Přesněji řešeno jsou opakované hry speciálním případem extenzivních her. Extenzivní hry jsou hry, které se hrají na kola. Příkladem můžou být třeba šachy, ve kterých v každém kole hraje pouze jeden z hráčů.
- Definice extenzivní hry
Extenzivní hrou rozumíme uspořádnou čtveřici Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (N,H,P,u_i)} , kde je množina hráčů je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle N} .Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle H} je množina posloupností, které splňují tři podmínky a to, že Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon \isin H} , kde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \epsilon} je prázdná množina. Další podmínkou je, že Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (a^k)_{k=1,...,K} \epsilon H \Rightarrow \forall L<K : (a^k)_{k=1,...,L} \epsilon H } a v případě, že nekonečná řada Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (a^k)^\infty_{k=1}} skládá z řad takových, že Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (a^k)_{k=1,...,L} \epsilon H} pro všechna Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle L} potom i Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (a^k)^\infty_{k=1} \epsilon H} . Takovou množinu nazýváme množinou historíí a její prvny historie, budeme značit Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h} .Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K} bude potom nejvyšší Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle L} pro něž platí Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h \epsilon H} . Toto číslo budeme nazývat počtem kol. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(h)} je funkce hrajících hráčů, kde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h} je již známá historie(v případě, že jsme v kole Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle L} , potom platí Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle h=(a^k)_{k=1,...,L-1}} . Tedy obor hodnot Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle H_P(h) = \{N,k\}} , kde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k} značí konec hry. Historie, pro které platí Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(h)=k} budeme nazývat konečné, jejich množinu budeme značit Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Z} a jednotlivé strategie Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle z,z \epsilon Z} . Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u_i(z),i \epsilon N} je výplatní funkce hráče Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} na množině konečných historií. Podle této definice máme hru, která se hraje v Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K} kolech a v každém kole hraje konkrétní počet hráčů. V každém dalším kole hráčihrají podle toho, co se už odehrálo. Příkladem může být vstup konkurence na monopolní trh.
- Definice profilu strategií
Profilem stragií v extenzivní hře Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (N,H,P,u_i)} hráče Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i \epsilon N} je funkce Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A_i(h)} . Definiční obor této funkce je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle D_{A_i}(h)=\{h \epsilon H:P(h)=i\}} . Výstup hry se potom rozumí funkce Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle O(A_1,...,A_n) = z,z \epsilon Z} .
- Definice Nashovy rovnováhy v sekvenční hře
Nashhovou rovnováhou v sekvenční hře Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (N,H,P,u_i)} se rozumí profil strategií Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A^*} takový, že pro každého hráče Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i \epsilon N} platí Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle u(O_i(A^*))\geq u(O(A^*_i,A_i))} , kde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle A^*_i,A_i} znamená, že všichni kromě i-tého hráče hrajou danou strategii.[4]
Odkazy
- ↑ CHVOJ, M. Pokročilá teorie her ve světě kolem nás Praha : Grada, 2013, ISBN 978-80-247-4620-3.
- ↑ PETRŽELKA, J. Opakované hry s neúplnou informací. Masarykova univerzita: Přírodovědecká fakulta [online]. 2017 [cit. 2020-06-07]. Dostupné z: https://is.muni.cz/th/qc0jx/PetrzilkaDP.pdf
- ↑ MAŇAS, M. Teorie her a její aplikace. Praha : SNTL, 1991, ISBN 80-03-00358-X.
- ↑ FRIEDMAN, J.W. Game Theory with Applications to Economics. (Second edition). New York : Oxford University Press, 1991, ISBN 0-19-506355-4.