Systatické hraní rulety
Zadání
- Název simulace: Systematické hraní rulety
- Předmět: 4IT495 Simulace systémů (LS 2013/2014)
- Autor: Písařík Marek (XPISM00)
- Typ modelu: Monte Carlo
- Modelovací nástroj: MS Office Excel 2010
Definice problému
Kasinovou hru ruleta je možné hrát náhodně, dle oblíbených čísel, intuice, či pomocí systematického vsázení. Existují 2 typy rulet. Francouzská (čísla 1-36 + neutrální políčko 0), či Americká ruleta (čísla 1-36 + 2x neutrální políčka 0 a 00). Matematickou výhodu rulety tvoří právě neutrální políčka, proto je vhodné si vždy zvolit pro hraní první typ. V každém kole vhodí krupiér kuličku v opačném směru, než je otáčení rulety. Hráči mohou vsázet na nespočet možností, jak dané kolo dopadne.
Možné sázky:
- číslo (popř. dvojice/čtveřice sousedících čísel)
- řada (popř. dvojice sousedících řad)
- sloupec
- tucty
- barva (červená/černá)
- sudá/lichá
- 1-18/19-36
Ve své simulaci se zaměřím na problematiku systematického sázení zejména na možnosti s 50% pravděpodobností (vyjma nuly) tedy červená/černá, sudost/lichost atd. Na tyto možnosti lze sázet dle matematických posloupností. U tohoto typu hraní je nezbytné disponovat dostatečně vysokým rozpočtem, který pokryje i málo pravděpodobnou řadu stejných hodnot.
Systémy:
- Martingale systém: vybereme si barvu a neustále na ní sázíme dvojnásobné částky, dokud daná barva nepadne, až ano. Poté budeme +1 násobené hodnoty (řada: 1,2,4,8,16,...)
- D‘ Alembert systém: funguje na stejném principu jako předchozí, jen při padnutí naší barvy nezačínáme od 1násobku hodnoty, nýbrž pouze o jednu hodnotu níže (tedy v případě že vyhrajeme v situaci, kdy sázíme 16ti násobek další kolo nesázíme 1násobek, ale 8mi násobek)
- Fibonacciho systém: Opět se jedná o systém podobný výše uvedeným, nicméně se vsází dle Fibonacciho posloupnosti, tedy vždy součet
Cíl simulace
V práci tedy budu simulovat náhodnost rulety, přičemž budu aplikovat všechny 3 systémy sázení. Vstupem do systému bude rozpočet, který na hru mám. A tedy v případě, že přijde smolně dlouhá série, na kterou rozpočet nebude stačit, hra končí a uživatel přišel o všechny peníze. Výsledkem bude dosažená částka na konci cyklu a tedy zhodnocení všech variant. Cílem simulace je tedy zhodnocení, který systém je nejvhodnější pro zadaný rozpočet. Nejvhodnějším se rozumí, při kterém dosáhnu s největší pravděpodobností nejvyšší výhry (pokud vůbec nějaké). posledních dvou hodnot posloupnosti (řada: 1,1,2,3,5,8,13,21,...)
Metoda
Jako nejvhodnější metodou pro řešení tohoto problému je právě metoda Monte Carlo. Důvod vhodnosti vychází z podstaty této metody a tedy z generování pseudonáhodných čísel, což přesně kopíruje realitu, kterou se snažíme simulovat. Generování čísel nahrazuje vhozenou kuličku do prostoru točící se rulety. Druhou možností, jak se dobrat k výsledku zkoumání je využít některé online kasino, ve kterém se dá nanečisto vyzkoušet hraní rulety bez nutnosti vložit peníze. Tento způsob je nicméně časově velmi náročný a proto byla zvolena metoda Monte Carlo v prostředí MS Office Excel 2010.
Model
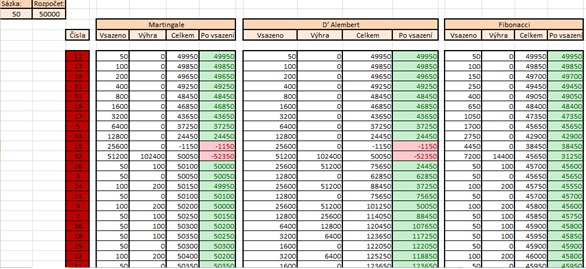
Model zachycuje dění na ruletě, tedy generuje pro každé „kolo“ pseudonáhodnou hodnotu v intervalu <0;36>, která reprezentuje políčko, do kterého padne kulička. Tyto hodnoty jsou následně využívány pro simulaci sázení dle 3 zvolených systémů, tedy Martingale, D‘ Alembert a Fibonacci. Všechny systémy se hrají na stále stejnou zvolenou variantu s 50% procentní pravděpodobností výhry (vyjma nuly), v případě naší simulaci se jedná o sázky na sudost padnuté hodnoty. Každý ze systémů má svůj vlastní sloupec s vypočtenými hodnotami. Pro každou metodu nás zajímá:
- Kolik dané kolo vsázíme na námi vybranou barvu/sudost…
- Kolik jsme dané kolo vyhráli (pokud vůbec)
- Jaký je náš celkový stav konta po odehraném kole
- Jaký je náš stav konta po provedení sázky (tedy jestli máme ještě rozpočet na provedení sázky)
Následující obrázek zachycuje simulaci jednoho cyklu: