Phyllotaxis

Project name: Phyllotaxis

Class: 4IT496 Simulation of Systems (WS 2016/2017)

Author: Bc. Naďa Bednárová

Software used: NetLogo

Introduction

Phyllotaxis is the repeated production of similar elements (leaves, petals) on the tip of a plant, producing a regular pattern. These arrangements of elements fall into two categories - creating one leaf at a time in distichous or spiral mode (following Fibonacci series or golden mean) or creating two leaves simultaneously at the same height. In this simulation I will study the first category.

According to Douady and Couder, there are three main approaches to the study of the origin of leaves arrangement.

Geometrical Approach

This approach studies the geometry behind leaves arrangement without trying to explain why or how exactly these patterns are formed.

The simplest model of the formation of phyllotactic patterns (for example in sunflowers or daisies) uses a special form of Fermat’s spiral equation. The formula was originally proposed by Vogel in the following format :

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \phi = n \times 137.5^\circ }

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle r = c \times \sqrt{n} }

Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\textstyle \phi } represents the angle between the reference direction (direction of the first floret) and n-th floret and is calculated as a product of n (denoting the number of a floret in given order) and angle between two subsequent florets. In order to get the Fibonacci sequences, the golden angle of approximately 137.5 degrees is used. Finally, r is the distance between the middle (capitulum) and the center of given floret, giving the parameter c, so called "growing factor" .

Fibonacci sequence (FS) is the following sequence of numbers : 1, 1, 2, 3, 5, 8, 13, 21, 34 ... , where each number is a sum of two previous numbers. Using simulation we can verify that the spiral patterns formed on a flower using golden angle as a distance of two subsequent petals create Fibonacci sequence, such that the number of spirals formed by leaves/petals in one direction is a number from the Fibonacci sequence; the number of spirals in the other direction is the number that follows in FS and the approximation of the intersections of these two spirals (another set of spirals) can form their sum, thus the third number of FS . See the comparison of model vs. reality for examples.

Dynamics of Growth

This approach studies the dynamic principles behind morphogenesis forming phyllotactic structures. A basic dynamic model of leaves formation from the meristem was first proposed by Hofmeister in 1868. He observed that small protrusions, called primordia, are formed in the apical region of a plant, where each primordium is created in a place where it has the most space available for its growth (e.g. to be able to catch the most of sun rays) .

Physiology of The Apical Meristem

In order to determine the physical processes responsible for the creation of phyllotactic patterns in plant's leaves or flower petals, different theories about interaction of primordia have been studied. These theories are based on either a diffusion of inhibitors, a reaction diffusion process (Turing), or a contact pressure. The interaction between primordia creates a process of repulsion or inhibition and it uses complicated dynamic equations. However, none of the theories gives a 100% correct model.

Model of Douady and Couder

This model is based on the experiment done by Douady and Couder on a horizontal teflon dish filled with silicone oil placed in a vertical magnetic field . The primordia are simulated by drops of ferrofluids that are periodically placed in the middle of the dish on given intervals T. The drops spontaneously move in the magnetic field away from the center of the dish. Every new drop is repeled from both the existing and the previous ones, causing it to move in the direction with minimum repulsive energy. The model of phyllotaxis inspired by this experiment combines previous dynamical and physiological models and creates patterns that can be studied by geometrical approach. It also allows various modifications, for example of the function of repulsive energy.

Goals

Goal of the simulation in NetLogo is to create a model of formation of the arrangement of leaves based on different parameters configuration (number and size of the leaves, starting angle, distance etc.). Furthermore, some of above mentioned theories about morphogenesis / meristem growth will be simulated and Fibonacci sequence creation in phyllotactic patterns will be tested.

Simulation

I created 3 simulations in NetLogo-5.3.1. First based on geometrical approach, second is a simple diffusion model with the same adjustable parameters as in the first one (also with a 3D model) and the third one is a dynamic model based on Douady and Couder approach.

Spiral Model

This model follows the geometrical approach described above, which means that it starts with the first leaf in the middle and then creates a new leaf at position Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\textstyle x = r \times \cos{\phi} } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\textstyle y = r \times \sin{\phi} } . We can then observe how different starting angles and distance parameters c change the pattern of the flower .

Key Parameters

There are two functions, setup_spiral and do_spiral. The first one sets the environment and variables, while the other one periodically creates the leaves using equations described above.

Parameters that we can set are:

• angle - the distance between two following leaves
• leaf-size - the size of each leaf
• dist - the distance parameter c
• dynamic-leaf-size - in case dynamic leaf size is turned on, the size of leaves gradually increases with the distance from the center

Diffusion Model

The diffusion model is based on a principle similar to a spiral, which means that similar parameters are set up, except that the leaves are created in the middle/center and they gradually move away in the direction of the defined angle. This model is a preliminary for the next model, where the original angle is not defined, but rather created dynamically.

Key Parameters

There are two functions, setup_diffuse and do_diffuse. On every tick, the main function do_diffuse creates one new leaf in the center with the orientation angle multiplied by ticks, which means that the first leaf will have the orientation equal to the original angle and every next leaf will have the same angle distance from the previous one. Furthermore, in every step, all existing leaves move in their direction by the distance set in dist.

Parameters that we can set are:

• angle - the distance between two following leaves
• leaf-size - the size of each leaf
• dist - the distance by which a leaf moves in every step in a given direction
• dynamic-leaf-size - same as in the previous model

Dynamic Model

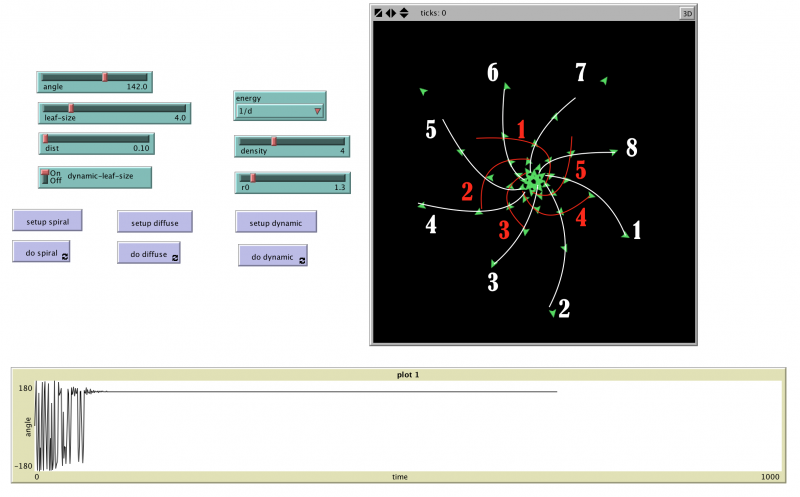
According to the study by Douady and Couder , unlike in the experiment, where the drops are placed in the middle of the dish, the model contains a central region representing the apex of a plant stem with radius rc (in our case same as r0). Primordia are created on the edge of this region, specifically on the place with the lowest repulsive energy E, which is the sum of repulsive energies of all already existing leaves. To calculate the energy, we need to create a potential primordia around the edge of the central region, called primordia also in the simulation code. These potential leaves can have different density around the apex, depending on how precise calculation is required. Then the energy E is calculated for each potential primordium and the one with minimal repulsive energy is transformed into real leaf.

Key Parameters

There are again two functions, setup_dynamic and do_dynamic. The important thing is that in setup_dynamic we set the parameter converg that is being plotted in order to study the angle representing the variable distance between two following leaves. As described in the model, the angle should gradually stabilise itself and converge to a value. In the do_dynamic method Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\textstyle 360 \times density } the potential primordia are created around the central circle with radius r0 and heading in the direction of the vector connecting the point (0,0) - center of the circle - with the center of given primordia. Afterwards the minimum energy is calculated using two different equations:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle  E = \sum_{i=1}^N 1 / d_i }

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle  E = \sum_{i=1}^N 1 / d_i^3 }

Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\textstyle d_i, i=1..N} is the distance of the given primordium from i-th leaf.

After calculating the energy affecting each primordium, the one with a minimum energy is selected and transformed into an actual primordium/leaf, as described above. All leaves then move (on every tick) with a gradual acceleration in the given direction using velocity equation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\textstyle V(r) = V_0 \times r / r_0 } , which means that the step of a particle with distance r from the center will be dist (the original size of one step) times r, divided by r0 (radius of the center). To make the model copy real processes, any further reorganization between particles based on repulsive energy isn't allowed.

We can set the following parameters:

• leaf-size - the size of each leaf
• dist - the distance parameter, can be understood as original velocity
• density - is the precision of calculation, meaning how many potential primordia there are around the central apex (360 up to 3600, thus density 1 up to 10; where for the density of 10 each degree contains 10 possible primordia)
• rc or r0 is the radius of central apex and the starting distance from the center for all leaves
• energy - total energy affecting given primordia - options Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\textstyle 1 / d } or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\textstyle 1 / d^3 }

As we can see in the following model, the pattern formed created Fibonacci sequence of 5 and 8 spirals and the angle that it converges towards is oscilating around 137.5 degrees (cca. +/- 0.2).

Model vs. Reality

As explained in the previous chapter, we can use the simulation to verify the hypothesis of Fibonacci sequences in spiral patterns on a flower/plant. First, we can see on the first random picture of Dahlia that a number of purple spirals (8) + a number of black spirals in the other direction (13) give us the sum of 21 equal to number of white spirals. All three numbers are subsequent Fibonacci numbers.

Second, we can test the same hypothesis in NetLogo, using our models. The following two patterns (2D and 3D) were created while playing with parameters to make the picture as similar to the real flower as possible.

By modifying the original angle of 137.5 degrees, similar spiral patterns were formed, but the numbers now did not follow the Fibonacci sequence.

Conclusion

Three different approaches have been described and implemented to test the formation of the phyllotactic patterns. I tested different parameters to create petals/leaves arrangements that resemble real flowers and follow the same Fibonacci numbers. However, in order to create a simulation, we have to neglect many parameters participating in the real process. Since there are many different theories about the formation of different phyllotactic patterns, the scope of this work was not enough to cover more of them. Nevertheless, the topic is very interesting and definitely a good subject of research for scientists, as well as for general public.

Possible Extensions

Few possible future model extensions:

• Energy could depend only on certain modifiable number of neighbouring leaves.
• Different energy equations could be tested.
• Different velocity functions can be tested.
• Other approaches can be modeled.

Code

File:2017BednarovaPhyllotaxis.nlogo