Přestupní stanice metra

Tato stránka je slouží jako výzkumná zpráva k simulaci představující semestrálním projekt pro předmět 4IT495 Simulace systémů (LS 2011/2012).

• Název simulace: PŘESTUPNÍ STANICE METRA
• Předmět: 4IT495 Simulace systémů (LS 2011/2012)
• Autor: Martina Čižinská
• Typ modelu: multiagentní
• Provedeno v: NetLogo 5

Definice problému

Model simuluje chování davu cestujících na přestupní stanici metra. Na takovéto stanici se vždy nachází obrovské množství lidí. Když se zde vyskytuje málo přestupních eskalátorů, začínají se tvořit se fronty až davy lidí, které velmi zdržují a cestující téměř po sobě šlapou.

V metru (např. stanice Muzeum na trase C v Praze) se sice často nachází i přestupní vestibuly, které také umožňují přestup na jinou barvu trasy metra, avšak tento přestup je často velmi zdlouhavý nebo o této možnosti řada cestujících ani neví a proto jej moc nevyužívají. V mnoha případech by dle mého názoru vyšel přestup přes vestibul možná i rychleji s porovnáním s frontami, které se tvoří u běžných přestupních eskalátorů. V tomto modelu není zahrnuta vlastnost pomalého přestupu, tudíž vestibul není označen jako pomalá varianta přestupu a slouží jen jako přestupní stanice pro ty cestující, pro které představuje nejbližší nebo nejméně frekventovaný východ pro přestup.

Podobná situace nastává, když se přestupní eskalátory vyskytují jen na jedné polovině celého metra. To cestující také velmi zdržuje, obzvlášť ty spěchající. Navíc se na přestupní stanici vždy nacházejí cestující, kteří chtějí přestoupit na jinou barvu trasy metra a cestující, kteří již na své barvě trasy jsou a čekají jen na přijíždějící metro. A toto je další důvod, proč se začíná tvořit zmatek, jelikož si všichni navzájem překážejí. V modelu jsou tedy zahrnuti cestující, kteří hodně spěchají, cestující, kteří nespěchají vůbec a běžní cestující, kteří čekají na příjezd metra. Tuto stručně shrnutou situaci a problém bych právě chtěla prezentovat touto simulací.

Vyhodnocovaly by se tyto parametry:

• frekvence využití východů pro přestup při určitých nastavených parametrech týkajících se cestujících
• čas (počet tiků), za který by všichni cestující přestoupili na jinou barvu přestupní stanice metra (tj. čas, za který všichni spěchající a nespěchající agenti splní svůj primární konečný cíl).

Tím by se zjistilo, která nastavená situace modelu byla nejefektivněji využívaná a nejrychlejší.

Shrnutím: simulovaný model představuje, jak by vypadala situace, když by:

• všechny přítomné eskalátory byly obousměrné/jednosměrné
• se zvýšil/snížil počet přestupních eskalátorů - 1, 2 nebo 3 eskalátory (jednosměrné/obousměrné)
• cestující využívali/nevyužívali pro přestup vestibul stanice metra - otevřený/zavřený vestibul
• se zvýšil/snížil počet běžných cestujících či spěchajících/nespěchajících cestujících
• se změnil poměr spěchajících/nespěchajících cestujících
• se změnila rychlost spěchajících/nespěchajících/běžných cestujících
• se zvýšila/snížila šance ušlapání nespěchajících cestujících spěchajícími cestujícími
• se zapnula/vypnula možnost zabíjení nespěchajících cestujících spěchajícími cestujícími

Metoda

Simulační prostředí programu NetLogo 5 jsem si zvolila pro vytvoření simulace hned z několika důvodů. V modelu je definováno několik agentů, kteří reagují na prostředí a stavy ostatních agentů. Každý z nich má stanovený svůj cíl, který se snaží plnit. Pomocí několika mnou vytvořených algoritmů je ovlivňováno jejich chování, reagující na momentální stav prostředí a stavy agentů. Jedná se tedy o komplexní systém a multiagentní systém, který je vhodné řešit např. pomocí již zmiňovaného programu NetLogo.

Jelikož jsem se s NetLogem setkala již v minulém zimním semestru 2011/2012 v předmětu Komplexní systémy (4IZ636) vyučovaném zde na VŠE, byl pro mne tento simulační program hned jasnou volbou. NetLogo disponuje obrovským množstvím možností. Má intuitivní programovací jazyk a umožňuje uživateli pozorovat simulaci během jejího chodu. Díky sběru dat pomocí grafů, histogramů apod. je pak možné si vytvořit detailní statistiky, které pomohou zjistit, jak byla navržená simulace efektivní a co je potřeba dále změnit či ponechat neměnné. Možnost změny parametrů umožňují například různé posuvníky, přepínače apod., což znamená, že uživatel nemusí definovat hodnoty napevno, nýbrž v rozmezí určitého intervalu a pomocí těchto pomocných nástrojů hodnoty následně měnit, což lze i za běhu simulace, když to kód umožňuje.

Živou simulaci v metru jsem ani neuvažovala, jelikož by se jednalo o téměř nemožný úkol. Na přestupních stanicích se nachází takové množství lidí, jež pozorovatel (tedy já) nemůže kompletně zachytit a dosáhnout tak objektivních výsledků.

Detailní popis modelu

Prostředí simulace modelu v programu Netlogo 5

Popis prostředí

Svět simulace má tvar obdélníku a jeho rozměry činí 51x25 patches. V prostředí modelu se nachází:

• 2 vagony metra vždy se 6 dveřmi - Vagony se nijak nemění, pro jednoduchost simulace se jedná jen o jeden příjezd metra v obou směrech
• 6 eskalátorů a 1 vestibul - Dohromady 7 přestupních východů.
• cestující - spěchající, nespěchající, běžní a zabití cestující

Všechny zmíněné prvky světa představují agenty, tudíž se více informací nachází v odstavci Agenti.

Popis uživatelského prostředí

• Posuvník number-of-normal-passengers - Nastavuje počet běžných cestujících, kteří nastupují do metra.
• Posuvník number-of-passengers - Nastavuje počet spěchajících a nespěchajících cestujících, kteří přestupují na jinou barvu trasy metra.
• Posuvník percentage-of-hurries - Nastavuje procentuální poměr spěchajících a nespěchajících cestujících.
• Posuvník speed-of-hurries - Nastavuje rychlost spěchajících cestujících.
• Posuvník speed-of-no-hurries - Nastavuje rychlost nespěchajících cestujících.
• Posuvník speed-of-normal - Nastavuje rychlost běžných cestujících.
• Posuvník number-of-escalators - Nastavuje počet otevřených eskalátorů.
• Přepínač two-way-escalators - Zapíná/vypíná obousměrné eskalátory.
• Přepínač use-vestibule - Zapíná/vypíná možnost přestupu přes vestibul metra.
• Posuvník chance-of-trampling/killing - Nastavuje procentuální šanci ušlapání nespěchajících cestujících spěchajícími cestujícími.
• Přepínač hurries-killers - Zapíná/vypíná možnost zabíjení nespěchajících cestujících spěchajícími cestujícími.
• Přepínač stop-with-hurries - Zapíná/vypíná vypnutí simulace, jakmile bude počet spěchajících cestujících roven nule.
• Monitory [frequency] of exit 0/1/2/3/4/5/vestibul - Tyto monitory ukazují frekvenci využití exitu cestujícími, kteří přestupují na jinou barvu trasy metra.
• Monitor Left/Middle/Right side - Tyto monitory ukazují frekvenci levé, prostřední či pravé strany, kde se nacházejí eskalátory pro přestup. Sčítá se vlastně jen frekvence exitů pod sebou na určité straně.
• Monitor Final average frequency of exits - Ukazuje konečnou výslednou průměrnou frekvenci využití všech otevřených exitů pro přestup.
• Monitor Number of hurries/no-hurries/normal passengers/dead people - Tyto monitory mají využití zejména na počátku modelu. Znázorňují, kolik cestující od každého typu bylo nastaveno, kromě mrtvých cestujících. Ti se připočítávají během běhu simulace.
• Monitor Number of ticks (at the end) - Tento monitor ukazuje, po kolika ticích byla simulace ukončena. Tento počet je sice také znázorněn v okýnku světa modelu. Mne osobně se však zdálo přehlednější, když byl tento výsledný počet tiků znázorněn v monitoru.

Agenti (prvky modelu)

Cestující

• Spěchající cestující (hurries)
• Nespěchající cestující (no-hurries)

Spěchající a nespěchající cestující se na počátku nacházejí náhodně v metru, tudíž nejsou při nastavení modelu vidět. Lze je zaznamenat až po spuštění modelu, jakmile naleznou východ z metra v podobě dveří a vylezou ven hledajíce nejvhodnější eskalátor pro přestup.

• Běžní cestující (normal-passengers)

Běžní uživatelé jsou také vygenerováni náhodně a vyskytují se v prostoru metra, který se nachází mezi vagony.

• Ušlapaní/zabití cestující (killed-people)

Ušlapaní/zabití cestující jsou ti cestující, které ušlapali/zabili spěchající cestující.

Počet běžných cestujících, počet spěchajících a nespěchajících cestujících a jejich poměr je nastavován v posuvnících. Další vlastností cestujících, kterou je možnost nastavit na začátku modelu je jejich rychlost. Ta je pro každý typ cestujícího nastavována zvlášť v posuvnících. V modelu je také zahrnuta možnost ušlapání a zabití nespěchajících cestujících spěchajícími cestujícími. To je vyjádřeno procentuální šancí ušlapání a zapínáním/vypínáním spěchajících cestujících zabijáků.

Východy

Východy představují eskalátory a vestibul. Jejich rod (breed) je v modelu označen jako exits. Uzavřené východy jsou označeno rodem no-exits.

Přestupních eskalátorů existuje dohromady 6, avšak nepředstavují 6 jednotlivých eskalátorů. Jedná se vlastně o 3 eskalátory, které buď plní funkci jednosměrných, nebo obousměrných eskalátorů. V posuvníku se nastavuje počet otevřených eskalátorů v rozmezí 1-3 a v přepínači, zda se bude jednat o jednosměrný či obousměrný eskalátor. Celý princip eskalátorů tkví v tom, že eskalátory nacházející se pod sebou tvoří jakoby dvojici eskalátorů. Ta je buď tvořena 2 eskalátory jedoucími dolů na přestup, nebo 1 eskalátorem jedoucím dolů a nahoru, nebo dvěma eskalátory jedoucími nahoru na trasu, kde se nacházíme. Eskalátory, které jedou nahoru, neplní funkci východu pro přestup a v průběhu simulace se s nimi nepočítá. Jejich rod (breed) je změněn z východu (exit) na ne-východ (no-exit) a cestující tyto je pak zkrátka ignorují.

• Eskalátory jezdící nahoru i dolů (obousměrné eskalátory, exits a no-exits)

Obousměrné eskalátory jedou jen dolů pro přestup a nahoru na trasu metra, kde se v simulaci nacházíme.

• Eskalátory jezdící jen nahoru (jednosměrné eskalátory, no-exits)
• Eskalátory jezdící jen dolů (jednosměrné eskalátory, exits)

Jednosměrné eskalátory jedou buď jen nahoru na trasu, kde se simulace odehrává nebo jen dolů na přestup.

• Vestibul (exits/no-exits)

Vestibul také slouží pro přestup na jinou barvu stanice metra. V přepínači je možnost nastavení, zda bude pro cestující otevřen či uzavřen.

Dveře metra

Oba vagony metra disponují 6 dveřmi (breed = subway-doors), které slouží pro spěchající a nespěchající cestující jako východ z metra a pro běžné uživatele jako vstup do metra.

Chování agentů

Spěchající cestující

Spěchající cestující jsou v modelu označeni rodem hurries. Tito pasažéři představují cestující, kteří chtějí přestoupit na jinou barvu trasy metra. Jelikož se na počátku modelu nacházejí v metru, jejich prvním cílem a úkolem je nalézt nejbližší východ z metra (dveře metra). Jakmile se ocitnou venku z vagonu metra, mají nový cíl: nalézt nejbližší otevřený eskalátor pro přestup. Během plnění jejich cílů se vyhýbají různým překážkám: sami sobě a dalším druhům cestujících. Na tyto překážky reagují různě. Mohou například ušlapat nespěchající cestující v závislosti na nastavené procentuální šanci ušlapání nespěchajících, či je dokonce zabít, když je tato možnost povolena. V místě ušlapání nebo zabití cestujícího se obarví políčko na červeno. Jejich rychlost pohybu je nastavována v posuvníku v rozpětí od 0.1 do 1 po 0.1.

Nespěchající cestující

Nespěchající cestující jsou v modelu označeni rodem no-hurries. Tito pasažéři představují cestující, kteří chtějí přestoupit na jinou barvu trasy metra. Jelikož se na počátku modelu nacházejí v metru, jejich prvním cílem a úkolem je nalézt nejbližší východ z metra (dveře metra). Jakmile se ocitnou venku z vagonu metra, mají nový cíl: nalézt nejbližší otevřený eskalátor pro přestup. Během plnění jejich cílů mohou být ušlapání spěchajícími cestujícími v závislosti na nastavené procentuální šanci ušlapání, a když se v sousedství dotyčného ušlapaného nacházelo >= 6 spěchajících cestujících. Spěchající cestující je mohou dokonce i zabít, když je tato možnost povolena. Rychlost pohybu nespěchajících cestujících je nastavována v posuvníku v rozpětí od 0.1 do 1 po 0.1.

Běžní cestující

Běžní cestující jsou v modelu označeni rodem normal-passengers. Jejich hlavním a jediným cílem je nalézt nejbližší dveře metra a nastoupit do něj. Ovšem aby tento úkol mohli splnit, musejí počkat, až nebude ve dveřích metra žádný jiný cestující, aby se všichni neumačkali. Jejich rychlost pohybu je nastavována v posuvníku v rozpětí od 0.1 do 1 po 0.1.

Mrtví cestující

Tento agent představuje zabité nebo ušlapané nespěchající pasažery. Je označen rodem killed-people. Další funkci zde vlastně nemají. Jen po nich zbude červené políčko, že zde byl někdo zabit.

Eskalátory

Eskalátory mají v modelu označení buď rodem exits nebo rodem no-exits. Záleží, zda eskalátor funguje jako východ pro přestup a je otevřený nebo zda jede jen nahoru a je tím pádem jakoby zavřený. V případě otevření a role východu pro přestup je označen rodem exits, v opačném případě rodem no-exits. Exits slouží jako primární cíle spěchajících a nespěchajících cestujících nacházejících se v prostorách metra mimo vagon metra. Více informací o principu výskytu eskalátorů se nachází v odstavci Agenti (prvky modelu).

Vestibul

Vestibul je v modelu označen buď rodem exits nebo rodem no-exits. Když je vestibul otevřený představuje rod exits a slouží jako primární cíl spěchajících a nespěchajících cestujících nacházejících se v prostorách metra mimo vagon metra. V opačném případě je zástupcem rodu no-exits a nemá žádnou jinou funkci.

Dveře metra

Dveře metra jsou označeny rodem subway-doors. V modelu se jich nachází celkem 12 (6 nahoře a 6 dole). Slouží jako primární cíle pro spěchající a nespěchající cestující nacházejících se uvnitř vagonu metra a pro běžné pasažery, kteří chtějí nastoupit do metra.

Metody a algoritmy

• Algoritmus setup-exits

Tento algoritmus nastavuje počet exitů, které v modelu existují. Počet všech exitů dohromady je 7.

• Algoritmus set-free-exits

Tento algoritmus nastavuje eskalátory a vestibul jako otevřené. Nastavuje jim zelenou barvu, tvar čtverečku a orientační popisek, že jsou k dispozici cestujícím pro přestup.

• Algoritmus set-close-exits

Tento algoritmus nastavuje eskalátory a vestibul jako uzavřené. Nastavuje jim červenou barvu, tvar křížku a orientační popisek, že cestujícím nejsou k dispozici. Agenti typu cestující je ignorují.

• Algoritmus setup-subway-doors

Tento algoritmus vytváří dohromady 12 dveří metra. 6 dveří se nachází v horním pruhu vagonu metra a zbylých 6 dveří v dolním pruhu vagonu metra. Nastavuje dveřím bílou barvu a tvar čtverečku. Žádné dveře se nenastavují jako uzavřené, všechny jsou cestujícím k dispozici.

• Algoritmus setup-subway

Tento algoritmus nastavuje prostředí metra simulace modelu. Vykresluje vagony metra, které se nachází v horním a dolním pruhu světa, barvu pozadí perónu metra apod. U eskalátorů se pak následně nastavuje, zda budou obousměrné či jednosměrné v závislosti na zapnuté či vypnuté možnosti obousměrných eskalátorů. Vestibul se v této metodě pak řeší zvlášť.

• Algoritmus setup-passengers

Tento algoritmus vytváří všechny typy cestujících. Nastavuje celkový počet a rychlost všech existujících cestujících (kromě mrtvých pasažérů) a počítá z celkového nastaveného počtu spěchajících a nespěchajících cestujících jejich poměr. Všem cestujícím generuje náhodnou pozici, která je nastavena tak, aby se žádný cestující nepřekrýval s jiným cestujícím. Spěchajícím a nespěchajícím uživatelům je zde nastaveno, aby se při nastavení skryly, běžní cestující vidět jsou a skrývají se později (to má na starosti jiný algoritmus).

• Algoritmus check-min-exit

Tento algoritmus nastavuje spěchajícím a nespěchajícím cestujícím nejbližší východ.

• Algoritmus check-hurries-min-exit

Tento algoritmus nastavuje nespěchajícím cestujícím nejvhodnější východ. Pokud se v okolí jejich dosavadního nejvhodnějšího (zpočátku pro ně nejbližšího) východu nachází >= 6 spěchajících cestujících, jako nejvhodnější východ je pro ně nastaven východ s nejnižší frekvencí využití.

• Algoritmus check-min-doors

Tento algoritmus nastavuje spěchajícím a nespěchajícím cestujícím za cíl nejbližší dveře ve vagonu metra, kde se nacházejí.

• Algoritmus passengers-move

Tento algoritmus hýbe všemi cestujícími. Řídí pohyb všech cestujících. U spěchajících a nespěchajících cestujících zahrnuje vystupování z metra a přestup na jinou barvu trasy přes eskalátor popř. vestibul a u běžných cestujících vstup do metra.

• Algoritmus move-all

Tento algoritmus nastavuje cestujícím souřadnice jejich cíle (exitu/dveří). Slouží jak pro spěchající, tak pro nespěchající, tak i pro běžné cestující. Jestliže se na políčku před určitým cestujícím ve vzdálenosti jednoho políčka nebo ve vzdálenosti rovné jeho rychlosti nenachází jiný cestující (spěchající, nespěchající či běžný), skočí o takovou vzdálenost, kde je rovna nastavené rychlosti. V opačném případě pokračuje algoritmus dál: jestliže se 45° napravo před určitým cestujícím ve vzdálenosti jednoho políčka nebo ve vzdálenosti rovné jeho rychlosti nenachází jiný cestující (spěchající, nespěchající či běžný), skočí o takovou vzdálenost, kde je rovna nastavené rychlosti. V opačném případě algoritmus opět pokračuje dál a to úplně stejně jako předchozí podmínka se 45° napravo, jen s tím rozdílem, že se kontroluje pozice 45° nalevo od určitého cestujícího.

• Algoritmus get-off

Tento algoritmus má na starosti vystupování z vagonu metra. Pokud se cestující (spěchající nebo nespěchající) nacházejí u východu (dveří) z metra, je jim nestaven nejbližší exit pro přestup.

• Algoritmus go-away

Tento algoritmus řídí vstup spěchajících a nespěchajících cestujících na eskalátory pro přestup na jinou barvu trasy metra. Pokud se u cestujícího nachází exit pro přestup, zvýší se frekvence využití tohoto exitu o jedničku a cestující v modelu zemře. Jeho úmrtí se ovšem nepřipočítává k celkovému počtu mrtvých cestujících, jelikož nebyl zavražděn či ušlapán.

• Algoritmus go-to-subway

Tento algoritmus řídí vstup běžných cestujících do vagonu metra. Ovšem tento algoritmus je použit, a tím pádem je i vstup umožněn jen za předpokladu, že se v sousedství dveří nenacházejí žádní spěchající a nespěchající cestující. V případě, že je běžnému cestujícímu umožněno projít dveřmi vagonu metra, připočte se k frekvenci využití dveří metra jednička a běžný cestující zemře. Jeho úmrtí se opět nepřipočítává k celkovému počtu zemřelých cestujících, jelikož nebyl usmrcen jiným cestujícím.

• Algoritmus kill-other

Tento algoritmus má na starosti zabíjení cestujících, jestliže je tato možnost zapnuta v přepínači. Jestliže není vyčerpán počet nespěchajících cestujících, zabíjí spěchající cestující jen nespěchající, pokud se nachází před spěchajícím cestujícím zabijákem ve vzdálenosti rovné rychlosti zabijáka. Pokud se ve světě nenachází již žádní nespěchající cestující, spěchající cestující zabijí sami sebe navzájem, pokud se v jejich okolí nachází >= 6 spěchajících cestujících.

• Algoritmus change-to-killed

Tento algoritmus mění rod nespěchajících cestujících na rod zabitých cestujících.

• Algoritmus trample-passengers

Tento algoritmus řídí ušlapávání nespěchajících cestujících. Celý princip je založen na nastavené procentuální šanci ušlapání a na množství spěchajících cestujících, tj. >= 6 hurries, nacházejících se v okolí ohroženého nespěchajícího cestujícího.

Spouštění a běh simulace

Model simulace se nastavuje tlačítkem Setup. Nastavení parametrů simulace umožňuje několik vytvořených posuvníků a přepínačů v uživatelském prostředí modelu. Samotná simulace se spouští stisknutím tlačítka Go. Probíhá v tzv. ticích (ne kontinuálně) a má omezený průběh. Běží do té doby, než bude počet všech spěchajících a nespěchajících cestujících roven nule. Tj. po splnění jejich druhého primárního cíle, nalézt nejbližší východ pro přestup.

Omezení a předpoklady rozšíření modelu

V modelu se objevují určitá omezení. Lépe simulovaná situace by určitě vypadala například s těmito parametry:

• "více příjezdů metra" - V modelu je nyní naprogramovaný jen jeden příjezd metra. Kdyby bylo příjezdů více, všichni běžní cestující by se pak nehrnuli do obou vagonů metra a vagon by měl také omezenou kapacitu počtu cestujících, kteří do něj mohou nastoupit
• lépe nasimulované výstup a vstupy cestujících - I když je zde zahrnut algoritmus, že cestující přes sebe chodit nemohou, během chodu modelu to i přesto tak vypadá.

Jako možné rozšíření mne napadlo:

• více příjezdů metra
• nastavení omezené kapacity dveří u metra či exitů na přestup

Výsledky

Jelikož se v modelu nachází nesčetné množství variant nastavení parametrů simulace a výsledků, které by toho moc nevypovídaly, by bylo zbytečně mnoho, uvedla jsem zejména ty nejdůležitější situace s efektivními výsledky. Vybrala jsem ty nejtypičtější napevno nastavené parametry a různé varianty simulace modelu, u nichž jsem výsledky považovala za ty nejzajímavější, a které také nejlépe osvětlí řešenou problematiku modelu.

Logicky vydedukovatelné a neuvedené situace simulace:

• čím větší rychlost cestujících - tím dříve simulace skončí
• čím více cestujících - tím déle simulace skončí a tím větší frekvence exitů
• čím více spěchajících cestujících - tím více ušlapaných/zabitých nespěchajících cestujících

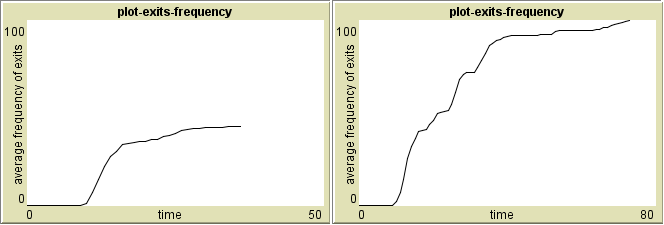
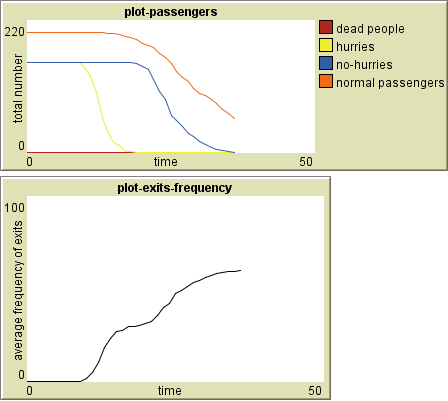
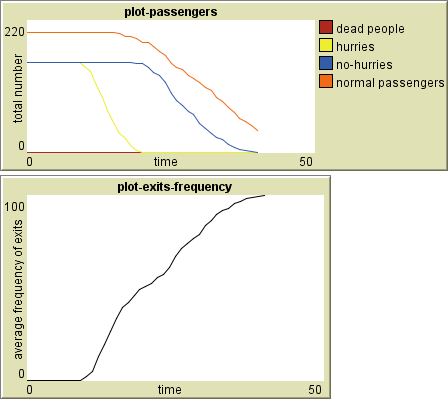
Pozorování č. 1: Frekvence využití exitů

Toto pozorování řeší orientační průměrnou frekvenci využití všech otevřených exitů pro přestup. Optimální využití činí cca 42 cestujících na 1 exit (podíl nastaveného celkového počtu přestupujících cestujících ku počtu všech exitů). Tj. ovšem téměř nereálné, proto se bude hledat nejefektivnější situace z tohoto pozorování spojená s nejefektivnější situací z pozorování č. 2, kde se pozoruje délka běhu simulace, tj. čas potřebný na přestup všech přestupujících cestujících.

Napevno nastavené parametry:

• počet běžných cestujících: 200
• počet spěchajících a nespěchajících cestujících: 300
• podíl spěchajících a nespěchajících cestujících: 50%
• rychlost spěchajících cestujících: 1
• rychlost nespěchajících cestujících: 0.5
• rychlost spěchajících cestujících: 0.3
• ušlapávání: vypnuto
• zabíjení: vypnuto

Obousměrné eskalátory

• Počet otevřených eskalátorů: 1 + uzavřený vestibul
  • průměrná frekvence exitů: 300 cestujících
  • Exit 0: 300
  • je vytěžován jeden jediný eskalátor na přestup na 100%
  • neefektivní situace

• Počet otevřených eskalátorů: 2 + uzavřený vestibul
  • průměrná frekvence exitů: 150 cestujících
  • Exit 0: 158
  • Exit 2: 142
  • téměř vyrovnané využití eskalátorů
  • méně efektivní situace - jen co se týče vyrovnané frekvence využití eskalátorů (číslo využití je ovšem veliké)

• Počet otevřených eskalátorů: 3 + uzavřený vestibul
  • průměrná frekvence exitů: 100 cestujících
  • Exit 0: 104
  • Exit 2: 91
  • Exit 4: 105
  • téměř vyrovnané všechny eskalátory pro přestup
  • efektivní situace

• Počet otevřených eskalátorů: 1 + otevřený vestibul
  • průměrná frekvence exitů: 150 cestujících
  • Vestibul: 45
  • Exit 0: 255
  • velmi přetěžovaný exit 0
  • málo využívaný vestibul
  • neefektivní situace

• Počet otevřených eskalátorů: 2 + otevřený vestibul
  • průměrná frekvence exitů: 100 cestujících
  • Vestibul: 53
  • Exit 0: 101
  • Exit 2: 146
  • mírně přetěžovaný exit 2 oproti exitu 0
  • vytěžované oba exity oproti vestibulu
  • málo využívaný vestibul
  • neefektivní situace obecně
  • efektivní situace, když by se nebralo v potaz, že je málo využívaný vestibul, jelikož v reálné situaci opravdu není moc využívaný
  • méně efektivní situace

• Počet otevřených eskalátorů: 3 + otevřený vestibul
  • průměrná frekvence exitů: 75 cestujících
  • Vestibul: 55
  • Exit 0: 53
  • Exit 2: 104
  • Exit 4: 88
  • vytěžovaný exit 2 i exit 4 oproti exitu 0
  • málo využívaný vestibul oproti 2 vytěžovaným exitům
  • neefektivní situace

Jednosměrné eskalátory

• Počet otevřených eskalátorů: 1 + uzavřený vestibul
  • průměrná frekvence exitů: 150 cestujících
  • Exit 0: 155
  • Exit 1: 145
  • téměř vyrovnaná zátěž eskalátorů - avšak velmi vysoká zátěž, co se týče celkového počtu
  • neefektivní situace

• Počet otevřených eskalátorů: 2 + uzavřený vestibul
  • průměrná frekvence exitů: 75 cestujících
  • Exit 0: 65
  • Exit 1: 81
  • Exit 2: 81
  • Exit 3: 73
  • téměř vyrovnané exity, i co se využití obou stran týče (jejich „přetěžování“ se vždy střídalo)
  • číslo celkového využití není už tak vysoké
  • efektivní situace

• Počet otevřených eskalátorů: 3 + uzavřený vestibul
  • průměrná frekvence exitů: 50 cestujících
  • Exit 0: 42
  • Exit 1: 49
  • Exit 2: 55
  • Exit 3: 60
  • Exit 4: 48
  • Exit 5: 46
  • nejvíce využívaná pravá část
  • nejméně využívaná prostřední část
  • levá strana je téměř stejně využívaná jako pravá část
  • méně efektivní situace - z hlediska přílišného počtu vstupů na přestup (drahé řešení)

• Počet otevřených eskalátorů: 1 + otevřený vestibul
  • průměrná frekvence exitů: 150 cestujících
  • Vestibul: 55
  • Exit 0: 110
  • Exit 1: 135
  • přetěžované exity (sami o sobě jsou téměř ve shodě)
  • málo využívaný vestibul oproti ostatním exitům
  • neefektivní situace

• Počet otevřených eskalátorů: 2 + otevřený vestibul
  • průměrná frekvence exitů: 60 cestujících
  • Vestibul: 56
  • Exit 0: 51
  • Exit 1: 54
  • Exit 2: 77
  • Exit 3: 62
  • efektivně využívaná levá část
  • mírně vytěžovaná pravá část, ale tj. dáno vestibulem, který se právě nachází na opačné pravé straně
  • efektivně využíván vestibul
  • efektivní situace

• Počet otevřených eskalátorů: 3 + otevřený vestibul
  • průměrná frekvence exitů: 42,86 cestujících
  • Vestibul: 54
  • Exit 0: 26
  • Exit 1: 22
  • Exit 2: 60
  • Exit 3: 50
  • Exit 4: 46
  • Exit 5: 42
  • přetěžovaná pravá část
  • málo využívaná levá část, jelikož se napravo nachází vestibul
  • efektivně využívaná prostřední část
  • efektivně využívaný vestibul v porovnání s ostatními východy
  • efektivní situace

Otevřený vestibul

Z monitoru frekvence vestibulu vidět, že cestující využívají vestibul ze všech východů nejméně, jakmile jsou k dispozici eskalátory pro přestup. Zajímavé je, že to samé se děje i v reálné situaci. Dalším zjištěním bylo, že čím méně exitů pro přestup je otevřeno, tím rychleji a strměji roste křivka grafu průměrné frekvence všech exitů. A je to vlastně i logické. Zástup cestujících se rychle nahrne např. k jedinému exitu a přestupuje.

Pozorování č. 2: Délka doby běhu simulace

Toto pozorování řeší problém, jaký by měl být efektivní počet funkčních exitů pro přestup na přestupní stanici metra, aby cestující co nejrychleji přestoupili (tj. nejkratší čas délky běhu simulace).

Výsledky tohoto pozorování jsou zejména ovlivněné těmito parametry:

• momentálním rozmístění uživatelů - proto byla simulace spuštěna vícekrát a vytvořila se průměrná hodnota výsledků
• počtem spěchajících a nespěchajících cestujících - logicky čím více spěchajících uživatelů, tím rychleji simulace skončí
• podílem spěchajících a nespěchajících cestujících - logicky čím více spěchajících uživatelů, tím rychleji simulace skončí
• rychlostí spěchajících a nespěchajících cestujících - logicky čím vyšší rychlosti cestujících, tím rychleji simulace skončí

Jelikož je většina těchto podmínek snadno rozumově vydedukovatelná, byly tyto parametry pro běh simulace nastaveny napevno.

Napevno nastavené parametry:

• počet běžných cestujících: 200
• počet spěchajících a nespěchajících cestujících: 300
• podíl spěchajících cestujících: 80%
• rychlost spěchajících cestujících: 1
• rychlost nespěchajících cestujících: 0.5
• rychlost spěchajících cestujících: 0.3
• ušlapávání: vypnuto
• zabíjení: vypnuto

Obousměrné eskalátory

• Počet otevřených exitů: 1 + uzavřený vestibul
  • výsledek: průměrně 70 tiků

• Počet otevřených exitů: 2 + uzavřený vestibul
  • výsledek: průměrně 39 tiků

• POČET OTEVŘENÝCH EXTIŮ: 3 + UZAVŘENÝ VESTIBUL
  • výsledek: průměrně 39 tiků
  • vítěz obousměrných eskalátorů

• Počet otevřených exitů: 1 + otevřený vestibul
  • výsledek: průměrně 70 tiků

• Počet otevřených exitů: 2 + otevřený vestibul
  • výsledek: průměrně 39 tiků
  • 2. místo u obousměrných eskalátorů

• Počet otevřených exitů: 3 + otevřený vestibul
  • výsledek: průměrně 39 tiků

Jednosměrné eskalátory

• Počet otevřených exitů: 1 + uzavřený vestibul
  • výsledek: průměrně 72 tiků

• Počet otevřených exitů: 2 + uzavřený vestibul
  • výsledek: průměrně 35 tiků
  • celkové 2. místo a 2. místo u jednosměrných eskalátorů

• Počet otevřených exitů: 3 + uzavřený vestibul
  • výsledek: průměrně 36 tiků

• Počet otevřených exitů: 1 + otevřený vestibul
  • výsledek: průměrně 70 tiků

• POČET OTEVŘENÝCH EXITŮ: 2 + OTEVŘENÝ VESTIBUL
  • výsledek: průměrně 34 tiků
  • celkový vítěz a vítěz jednosměrných eskalátorů - 1. místo

• Počet otevřených exitů: 3 + otevřený vestibul
  • výsledek: průměrně 36 tiků

Závěr

Závěrem bych chtěla shrnout a zhodnotit konečné výsledky simulace modelu. Co se týče pozorování č. 2: počet tiků běhu simulace, výsledky podobných situací (tj. např. situace lišící se jen otevřeným či uzavřeným vestibulem) byly víceméně téměř shodné. Výsledné efektivní řešení, tedy rozhodovalo hlavně pozorování č. 1. Jelikož je většina výsledků a zdůvodnění uvedena v předchozím odstavci Výsledky, uvedu a osvětlím zde zejména 2 hlavní nejdůležitější výsledky.

Celkový vítěz a vítěz jednosměrných eskalátorů

Vzhled prostředí (metra)

Celkovým vítězem, co se týče efektivního počtu otevřených exitů pro přestup, se stal model jednosměrných eskalátorů se 2 otevřenými eskalátory a otevřeným vestibulem.

Vyhrál díky:

• nejkratšímu průměrnému počtu tiků běhu simulace
  • 34 tiků
• efektivní využití jednotlivých exitů pro přestup
  • vestibul: 56
  • exit 0: 51
  • exit 1: 54
  • exit 2: 77
  • exit 3: 62

Zcela efektivně byla využívaná levá část s eskalátory. Pravá část byla oproti levé části mírně přetěžovaná, to je ovšem dáno polohou otevřeného vestibulu, který se nachází právě na opačné levé straně. Vestibul byl také efektivně využit. Průměrná frekvence využití všech exitů činila 60, což není vůbec špatné. Vyskytly se zde sice i lepší průměrné frekvence, avšak celkový počet otevřených exitů už byl zbytečně vysoký a v praxi by to vyšlo také příliš draze.

Vítěz obousměrných eskalátorů

Vzhled prostředí (metra)

Vítězem obousměrných eskalátorů se stal model se 3 otevřenými eskalátory s uzavřeným vestibulem. Průměrná frekvence exitů činila 100 cestujících, což je více než v případě celkového vítěze, proto jej také tento model neporazil. Co se týče frekvence využití jednotlivých exitů:

• exitem 0 prošlo 104 cestujících
• exitem 2 prošlo 91 cestujících
• exitem 4 prošlo 105 cestujících

Frekvence jednotlivých eskalátorů je tedy téměř vyrovnaná.

Reference

• NetLogo
• NETRVALOVÁ, Arnoštka. Úvod do problematiky multiagentních systémů [online]. Plzeň : ZČU. Dostupné online.

Kód

• File:Subway.nlogo

Přílohy

• File:Documentation.pdf