Kraus Lucie, xkral52 - Rozvozové časy - Monte Carlo

Tato stránka je slouží jako Výzkumná zpráva simulace "Rozvozové časy" k semestrálnímu projektu pro předmět 4IT495 Simulace systémů (LS 2013/2014) na VŠE v Praze.

Zadání

• Název simulace: Rozvozové časy
• Předmět: 4IT495 Simulace systémů (LS 2013/2014)
• Autor: Lucie Kraus
• Typ modelu: Monte Carlo
• Provedeno v: MS Excel 2013

Definice problému

Jsme v situaci, kdy máme údaje z eshopu poskytující suroviny k vaření, který sám rozváží svým kurýrem po Praze objednávky. Zákazník si může vybrat během objednání rozvozový čas (interval 2 hodiny). Nabízené dny k analýze jsou pondělí až sobota (o neděli není z managementu eshopu zájem) a rozvozové časy jsou intervaly dvou hodin: 8-10, 10-12, 12-14, 14-16, 16-18, 18-20, 20-22.

Cílem situace je zobrazit, které rozvozové časy jsou neztrátové a které jsou a o kolik.

Použitá výchozí data, pravděpodobnosti a pravděpodobnostní rozdělení vycházejí z reálných dat eshopu a dále se s nimi v simulaci pracuje.

Metoda

Tato simulace byla ideální pro metodu Monte Carlo (práce s čísly, nutnost nasimulovat každý den a každý rozvozový čas desetitisíckrát a více, pravděpodobnostní rozdělení). Vypracovaná v prostředí MS Excel 2013.

Model

Listy modelu:

• Start - první list modelu s editovatelnými parametry modelu
• Mezivýpočty - list s přehledem a výpočtem dalších parametrů nutný pro další postup (pro standardního uživatele nejsou určeny k editaci)
• Výpočet obj - vygenerování přibližného počtu objednávek pro každý den
• Výpočet den obj - vygenerování počtu objednávek pro každý rozvozový čas (seskupeno podle dní)
• Výpočet náročnosti - výpočet náročnosti každého rozvozového času
• Výpočet nákladů - celkový výpočet všech nákladů
• Výstup - přehled matematických výpočtů
• Výsledek - grafické a zjednodušené znázornění výsledků

Výchozí data

V modelu se pracuje s několika proměnnými, které jsou dány informacemi extrahovanými přímo z reality (data z eshopu).

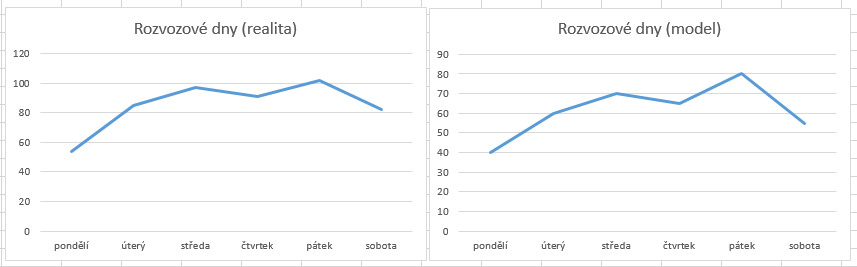
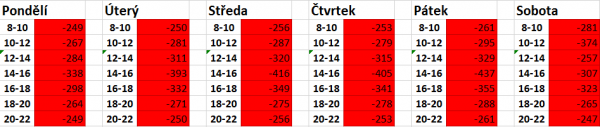
Počet objednávek pro jeden rozvozový den

Níže zveřejněný graf zobrazuje dlouhodobý vývoj počtu objednávek pro každý rozvozový den. Z této reality lze vyčíst mnoho informací:

• v pondělí si velice málo lidí nechává přivést zboží (začátek týdne, stres, není čas vařit)
• vrchol objednacích termínů je středa a pátek
• obliba sobotního termínu před obědem a večeří

Na graf bohužel nešlo stoprocentně použíz pravděpodobnostní rozdělení (viz čtvrteční propad), tj tyto informace jsou poskytnuty jako základ pro výpočet střední hodnoty normálního rozdělení přímo pro každý den v procentech.

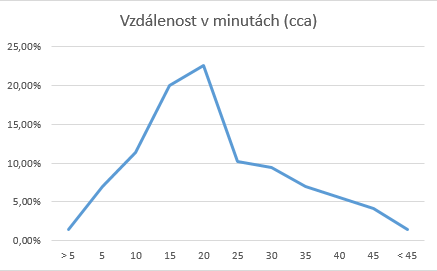
Vzdálenost ("Náročnost")

Vzdálenost je potřeba pro výpočet variabilních nákladů jako benzin. Graf z reality ukazuje, že takový vývoj má pravděpodobností rozdělení Beta. V modelu lze náročnost (vzdálenost) objednávek upravovat, například kdyby se eshop rozšířil i mimo Prahu do okolních vesnic atd, případně naopak zúžil svůj prostor.

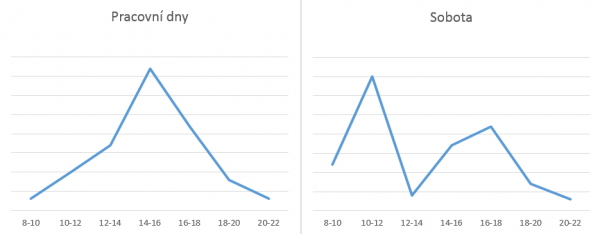
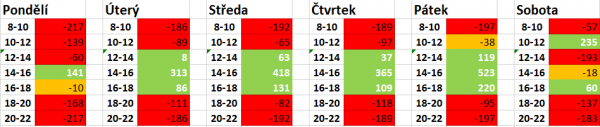
Poptávka po rozvozových časech

Graf zobrazuje současný vývoj poptávky po rozvozovém čase. Pracovní dny mají poptávku po rozvozových časech prakticky identickou, zatímco sobota má úplně jiné rozdělení (díky kterému nelze použít pravděpodobnostní rozdělení).

Editovatelné parametry

• Vzdálenost: Komplikovanost tras zadaná na stupnici 1 - 7 (jedna - velice jednoduchá, 7 - velice komplikovaná)
• Cena za dopravu zákazníkovi: Cena dopravného, které hradí zákazník (0 - 100 Kč, celá čísla)
• Průměrné náklady na 10 minut v autě (mezi 10 - 20 kč, průměr bývá kolem 14kč (výpočet založen na ceně benzínu 36 kč/litr, průměrná rychlost po Praze 35 km / h a spotřeba 6,5 l / 100 km) )
• Náklady na 1h práce (0 - 300 Kč)
• Maximální nákladnost jedné objednávky: maximální přípustná nákladnost jedné objednávky po odečtení dopravného atd. ( 0 - 100 Kč)

Jak model počítá

1. Nastaví se editovatelné parametry v Listu Start

2. Na základě ceny dopravy pro uživatele se vypočítají hodnoty pro normální rozdělení pro přibližný výpočet počtu objednávek za jeden daný den.

Střední hodnota se vypočítá:

=ZAOKROUHLIT(((100-[cena_dopravy])/100*[parametr_násobku_střední_hodnoty]+[parametr_přičtení])*[výchozí_hodnota_při_ceně_100_za_dopravu];1)

Směrodatná odchylka:

=ZAOKROUHLIT(((100-[cena_dopravy])/100*[parametr_násobku_směrodatné_odchylky]+[parametr_přičtení])*[výchozí_odchylka_při_ceně_100_za_dopravu];1)

3. V list Výpočet obj se vypočte počet objednávek pro každý den 29999x. Normální rozdělení bylo použito z výpočtů reality (střední hodnota je opravdu přibližný průměr objednávek).

=NORM.INV(NÁHČÍSLO();[střední_hodnota_z_kroku_2];[směrodatná_odchylka_z_kroku_2])

Ošetření pro extrémní hodnoty, které vygenerují číslo menší než 0:

=KDYŽ([výsledek_náhodného_rozdělení]<0;0;[výsledek_náhodného_rozdělení])

4. V listu Výpočet den obj dochází k rozdělení předběžného počtu objednávek za daný den do příslušných rozvozových časů

=ZAOKROUHLIT([předpokládaný_počet_objednávek_z_kroku_3]*([procento_pravděpodobnosti_daného_času]/100)*(1+(NÁHČÍSLO()*(3+3)-3)/10);0)

Část vzorce (1+(NÁHČÍSLO()*(3+3)-3)/10) generuje čísla jako 1,3 nebo -1,2, resp. hodnoty mezi -1,3 a 1,3. Tato část je tu kvůli náhodné odchylce od dané pravděpodobnosti rozvozového času (z listu Mezičas), aby výsledek nebyl přesně daný procentem a měl jistou odchylku.

5. Na základě počtu objednávek se vypočítají hodnoty pro beta rozdělení pro výpočet náročnosti rozvozu pro každý den.

Střední hodnota:

=[výchozí_střední_hodnota]+[hodnota_parametru_vzdálenost]

Směrodatná odchylka (-2 a -1 aby se udržel tvar beta rozdělení):

=KDYŽ([hodnota_parametru_vzdálenost];[výchozí_hodnota_odchylky]-2;[výchozí_hodnota_odchylky]-1)

6. Vypočte se náročnost objednávek pro každý rozvozový čas každého dne:

=ZAOKROUHLIT((BETA.INV(NÁHČÍSLO();[vypočtená_alfa];[vypočtená_beta];[min];[max])*100)/(((100-[cena_dopravy])/100)/[procentuální_snížení_díky_počtu_objednávek]+1);0)

Část vzorce (((100-[cena_dopravy])/100)/[procentuální_snížení_díky_počtu_objednávek]+1) ovlivňuje vygenerovanou beta náročnost. Dělí vygenerovaný výsledek číslem 1 až 1,33 (tj. snižuje výsledek až o 33%). Tento výpočet je zde kvůli faktu, že když je více objednávek (= cena za dopravu je nižší), cesty mezi objednávkami musí být logicky kratší.

7. Poté se v listu Výpočet nákladů spočítají náklady pro daný čas

=([vypočtená_náročnost_času_z_bodu_6]/10)*[průměrné_náklady_na_10_minut]*[počet_obj_daného_času]+([hodinové_náklady]*2)

8. V listu Výstup se už provádí pouze finální výpočty nákladovosti.

Nejdříve se spočítají příjmy z objednávek, které si můžeme odečíst z nákladů

=KDYŽ([průměrný_počet_objednávek_daného_času]=0;0;[průměrný_počet_objednávek_daného_času]*[cena_za_dopravu])

A poté se vypočtou zbylé náklady

=ZAOKROUHLIT(KDYŽ([průměrný_počet_objednávek_daného_času]=0;0;(([průměrné_náklady_na_objednávky]-[příjmy_z_ceny_dopravy])-([průměrný_počet_objednávek_daného_času]*[maximální_přípustné_náklady_na_obj]));0)

9. Finální pohled na výsledky barvami ovlivněný podmíněným formátováním.

Pokud je výsledná hodnota nula nebo záporná, stane se z ní kladná (je to zisk) a naopak.

=KDYŽ([průměrný_počet_objednávek_daného_času]=0;"no obj";[výsledné_náklady_času]*(-1))

Náhodná čísla & omezení modelu

Seznam náhodně generovaných čísel v modelu:

• v normálním rozdělení pro výpočet počtu objednávek jednoho dne (list Výpočet obj)
• v odchylce pro výpočet počtu objednávek jednoho rozvozového času z celého dne (list Výpočet den obj)
• v beta rozdělení pro výpočet náročnosti cest (list Výpočet náročnosti)

Omezení:

Model nevygeneruje například 1000 objednávek za den. Maximální počet objednávek je pro každý den dán násobkem ze základny pro výpočet objednávek (čísla střední hodnota 8, 12, 14, 13, 16, 11 a odchylka 2), tj model vygeneruje maximálně například v případě pátku a ceně za dopravu 0 normální rozdělení o střední hodnotě 80 a směrodatné odchylce 6.

Je to omezení, avšak management eshopu v příštích měsících neočekává více jak 100 objednávek za den, považuje ho za extrémní a velmi výjimečné číslo.

Zároveň nepočítáme s více řidiči a zisk z výsledků nepřerozdělujeme (zase rozhodnutí managementu).

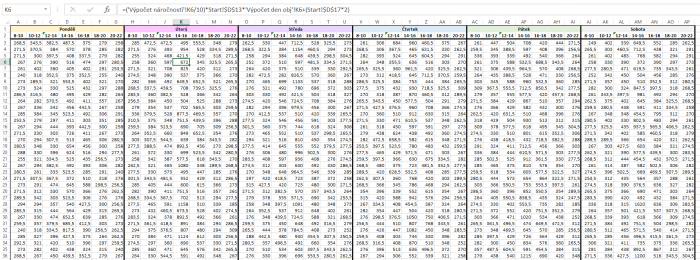
Výsledky

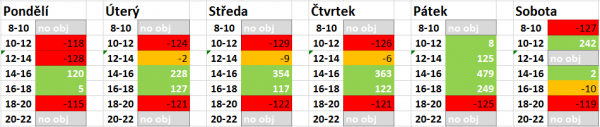
Výstupem je přehledná tabulka zobrazujicí rozvozové časy (zelené pozadí buňky), které nejsou prodělečné.

S výsledky simulace jde dále pracovat, avšak už záleží na v budoucnu stanoveném business modelu eshopu.

Způsoby dalších interpretací výsledků jsou vlastně tři:

• eshop bude jezdit pouze v časech, které jsou ve výsledné tabulce zelené (tj. v nich nemá ztrátu)
• eshop sečte zisk a rozhodne se v případě "přebytečného" zisku dotovat další rozvozový čas, ten nejméně ztrátový
• eshop sečte zisk a rozhodne se v případě "přebytečného" zisku dotovat další rozvozový čas, avšak takový, který by se mu hodil pro zjednodušení administrativy. Tj v případě výsledku níže zobrazených:

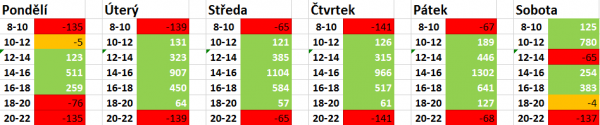
Příklad č.1:

• Vzdálenost: 2
• Cena za dopravu: 30
• Průměrné náklady na 10 minut: 10
• Náklady na 1h práce: 100
• Max nákladnost: 48

Tabulka zobrazuje zeleně neprodělečné časy. Pokud bychom chtěli přijmout jeden ztrátový čas (číslo určené vedením eshopu, ne modelem), nabízí se ihned sobota 18-20. Pokud se rozhodujeme pro zjednodušení administrativy, pravděpodobně by bylo chytřejší přijmout spíše čas v pondělí 10-12, protože by se pak veškeré pracovní dny rozváželo od desíti dopoledne a sobotu zachovat jako "výjimečný den".

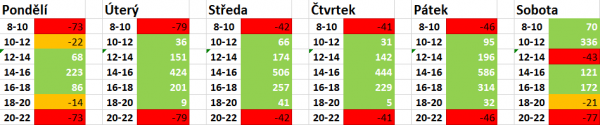
Příklad č.2:

• Vzdálenost: 2
• Cena za dopravu: 20
• Průměrné náklady na 10 minut: 10
• Náklady na 1h práce: 50
• Max nákladnost: 20

Zde se například rozhodneme z přebytečného zisku rozdělit 50. Možností je mnoho, nabízí se sobota 12-14 nebo 18-20, pondělí 10-12 a 18-20 a středeční až páteční večerní a ranní termíny. Kdybychom i zde chtěli uplatnit možnost zjednodušení administrativy, přijememe pondělní časy 10-12 a 18-20 a administrativa v eshopu bude jednodušší.

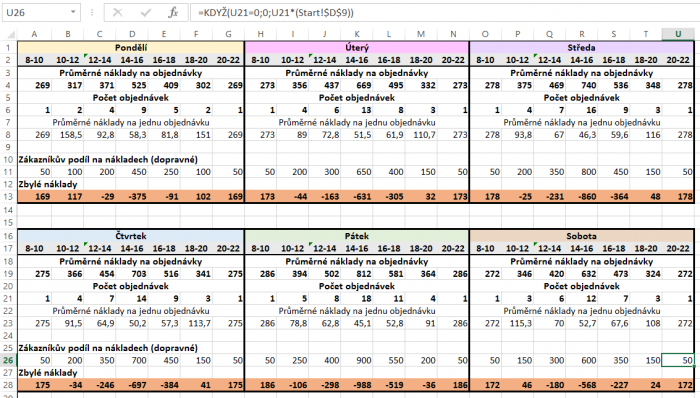
Výsledky relevantní pro náš eshop

Současný stav

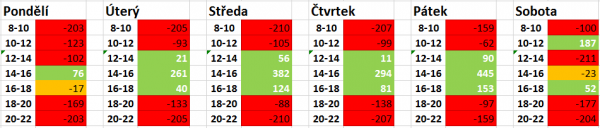
Parametry

• Vzdálenost: 2 (odpovídá náročnosti rozvozům po celé Praze)
• Cena za dopravu: 45
• Průměrné náklady na 10 minut: 14 (výpočet z průměru)
• Náklady na 1h práce: 120
• Max nákladnost: 10

Výsledek:

Z tabulky je patrné, že pondělní rozvozy nemají moc smysl (rozvážet pouze mezi 14-16h). Buď rozvozy v pondělí úplně zrušit anebo je dotovat ze zisku ostatních časů. V sobotu by se vyplatilo rozvážet jenom před obědem a večeří. Spojování časů do čtyřhodinových intervalů (10-14 a 14-18) bych nedoporučovala z marketingového hlediska (je rozdíl, jestli dostanu suroviny na oběd v 10h nebo 14h).

Akce doprava zdarma

Parametry

• Vzdálenost: 2
• Cena za dopravu: 0
• Průměrné náklady na 10 minut: 14
• Náklady na 1h práce: 120
• Max nákladnost: 10

Výsledek:

Z výsledku je naprosto jasné, že když se zákazník nijak neparticipuje na pokrývání nákladů na dopravě, maximální přípustná nákladnost na objednávku musí být vyšší než 10 Kč, jinak model nezobrazí prakticky ani jeden neprodělečný čas. Akce "doprava zdarma" má samozřejmě spíše marketingový význam a dramaticky zvyšuje počet objednávek.

Parametry

• Vzdálenost: 2
• Cena za dopravu: 0
• Průměrné náklady na 10 minut: 14
• Náklady na 1h práce: 120
• Max nákladnost: 42

Výsledek:

Když zvýšíme maximální nákladnost z deseti na 42 Kč, tabulka se změní a zobrazí neprodělečné rozvozové časy, které jsou podobného rozdělení jako při ceně za dopravu 45 Kč a maximální nákladnost 10kč. Takže rozdíl nákladů při akci Doprava zdarma je cca 32Kč na objednávku.

Extrémní hodnota 100 Kč

Parametry:

• Vzdálenost: 2
• Cena za dopravu: 100
• Průměrné náklady na 10 minut: 14
• Náklady na 1h práce: 120
• Max nákladnost: 10

Výsledek:

Model může nasimulovat poptávku při extrémní ceně za dopravu 100 Kč pro zákazníka ( v některých eshopech je dopravné i 170 Kč např). Zajímavý je výsledek modelu, který ukazuje profitabilní časy, protože za 100Kč dopravného se víceméně objednávka sama zaplatí a ještě je z ní i někdy profit, avšak objednávek je velice málo, nejvíc v pátek odpoledne - 6. A to rozhodně není vhodné pro marketingové účely a celkový obrat eshopu, i když na první pohled vypadá tabulka "šťastně zeleně".

Závěr

V modelu se zřetelně zobrazují neprodělečné rozvozové časy na základě zadaných parametrů. Při aplikaci současných dat ( Výsledky relevantní pro náš eshop - Současný stav ) je z modelu vidět, že se vyplatí v pracovní dny rozvážet mezi 12-18 hodinou v případě dotace pondělních časů. Na sobotu se musí kvůli jejímu rozdělení aplikovat speciální přístup, pravděpodobně rozvážet v dopoledních a odpoledních hodinách, ale ne v době oběda.

Model lze případně rozšířit například o více řidičů (přímo identifikovat "toto rozveze řidič 1, toto rozveze řidič 2), ovlivňování počtu objednávek promo akcemi (například Facebook kampaň) nebo omezeními ( "Minimální cena objednávky je 200 Kč") a o výnosnost objednávek přímo z jejich objemu ("objednávka za 600kč vs objednávka za 30 Kč"),

Kód

Odkaz na uloz.to

Odkaz na Dropbox

! Model má kolem 50 MB, tj se načítá velice dlouho a též dlouho přepočítává výsledky (generování přibližně 2,3 miliónů náhodných čísel).