Jellyfish problem
Contents
Introduction
American beaches are often guarded by lifeguard to safe people’s life when drowning. But drowning is not the only problem on the beach. Very often lifeguards must deal with jellyfish. Their population increases with higher temperature. Sometimes in the hottest days of august the water needs to be closed as the number of people stung by jellyfish overcomes hundreds.
Used software: NetLogo 6.0.2 to create the simulation and get the results and Excel 2016 tu summarize the result and come to conclusion.
Problem definition
The problem that lifeguard employer needs to solve is quite simple: How many lifeguards should be on the beach and where should they be placed? When does the water become too dangerous to swim there and it needs to be closed for public? The less lifeguard he must pay for, the better for employer but he can’t afford beach patrons feeling unsafe. Concerning drowning, one lifeguard can cover 400 meters of a beach but is he able to help all people stung by jellyfish in this area in time? When you get stung by moon jellyfish and take proper care of it within 5 minutes, there is high chance the pain goes away in next half an hour. But if you don’t treat it in time, the poison gets deeper under your skin and it can be painful for days. In such case beach patrons become really unhappy and most likely don’t come for holiday to this beach again. That’s why the lifeguards try to provide the best and fastest care as possible. This simulation is supposed to help employer decide about number of lifeguard on the beach in certain conditions and about the conditions leading to closing the water.
Background information
From years of experience it’s known that in temperature under 70 °F there are no jellyfish in the ocean (or just very few). As the temperature goes higher so goes higher the number of jellyfish. In temperature over 100 °F there might be hundred people stung by jellyfish on each 200 meters of the beach whereas in 80 °F there are just units of people.
Model
Model consist of 4 turtles (patrons, lazy-patrons, jellyfishes and lifeguards) and 2 kinds of patches (beach and ocean). Simulated world is 400 patches wide and 200 patches high which represents 400 meters of a beach (1 patch = 1 meter in reality).
Patrons and lazy patrons
To make the model realistic, there must be to kinds of people. In real world (USA) about 80 – 90% of people stay all day on the beach and don’t even enter the water, 10 – 20% of people is active and play in the water most of the day. That’s why there are “patrons” in the model, who can move all over the simulated world and their movement is random until they get stung by jellyfish. Each patron has defined step-size, rescue-time (countdown to the moment, when person’s injury gets serious) and chosen-guard (the nearest lifeguard the person will seek in case of getting stung). The rest of total amount of people is called “lazy-patrons” and they are just sunbathing on the beach all day and don’t move at all (they don’t play a role in simulation, just making the model looking like reality).
Jellyfishes
Purple creatures randomly moving in the ocean. Their number depends on the temperature.
Lifeguards: there are two lifeguards with fixed y coordinate (they are still on the beach) and adjustable x coordinate. If you set x coordinate the same for both guards, it works as if there is only one guard on the beach. They do not move during the simulation.
Ocean
Ocean is represented by blue patches and it covers ¾ of simulated world.
Beach
Beach is represented by light yellow color and it is situated in top quarter of simulated world. Anytime a jellyfish gets to the beach it dies.
Except of the turtles and patches, there are some global variables used in the model to countdown the time (simulation represent one lifeguard working day which is 9 hours = 32400 seconds), to count all people stung by jellyfish and number of seriously injured people. It also contains several procedures to make people and jellyfish move, to make people go for help and be helped and also some reporters.
Results
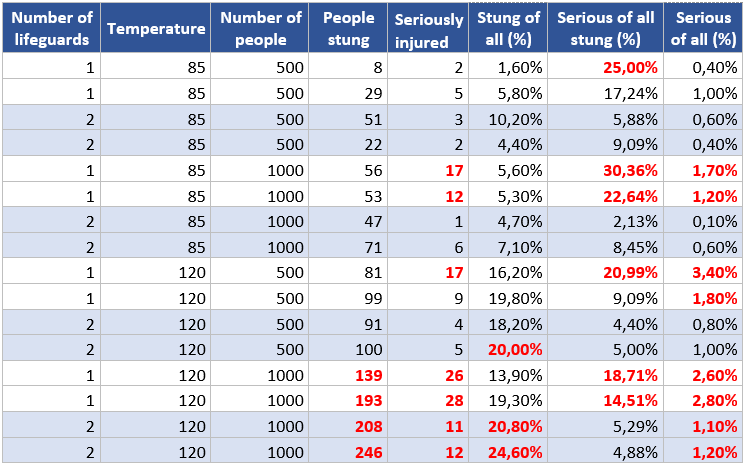
I’ve simulated 4 different combinations of temperature (85°F (normal), 120°F (extreme)) and number of people on the beach (500 (week day) and 1000 (weekend)) and compared the results with one lifeguard located in the center of a beach and 2 lifeguards evenly distributed on a beach. The results are summed up in following table:
It is obvious that having two lifeguards is safer but considering the price for second lifeguard there might be days when one lifeguard is enough. Let set some limits of people stung and seriously injured that are acceptable. These limits can be absolute or relative.
Absolute limits:
• Number of people stung by jellyfish <= 100
• Number of people seriously injured <= 10
Relative limits:
• Share of people stung by jellyfish from all people on the beach < 20 %
• Share of people seriously injured from all people stung by jellyfish < 20 %
• Share of people seriously injured from all people on the beach < 1 %
When we apply these limits on our result (highlighted in the table) we come to the following conclusion.
Conclusion
In the temperature 85°F during the week days it’s enough to have one lifeguard on the beach, the number of people stung is quite low and so even the number of those who are seriously injured is alarming. During the weekend and other busy days, there should be 2 guards even if the temperature is low. In extremely hot weather it gets much worse. Even if the beach is not too busy it still needs 2 lifeguards and in really busy days it might be better to close the water and only let people stay on the beach or swim in swimming pool nearby because the danger goes to high.