Dlouhodobé investování pro zajištění stability v důchodu na základě investičního portfolia

Zadání

• Název simulace: Dlouhodobé investování pro zajištění stability v důchodu na základě investičního portfolia

• Použitá metoda: Monte Carlo

• Použité prostředí: MS Excel 2007

• Autor: Petra Krečmerová

• Odkaz na zadání simulace: Zadání_xkrep00

Definice problému

Každý začínající i zkušený investor má při sestavování svého portfolia na paměti pravidlo, které je všem vštěpováno ve škole či z úst investičnÍho poradce. Diverzifikovat! V simulaci se předpokládá dlouhodobé portfolio, které zajistí stabilní finanční situaci v důchodu. K portfoliu je přistupováno pasivně, v tomto případě je doporučený poměr konzervativní a dynamické složky přibližně 25 % ku 75 %. Základními složkami portfolia budou akcie, dluhopisy a komodity. Akcie a dluhopisy jsou široce využívány pro negativní závislost jejich výnosů - jestliže se akciím daří, dluhopisy klesají a naopak. Moderní portfolio je však vhodné doplnit i o komodity, do portfolia bude vybrán jeden zástupce. Použitou měnou jsou dolary, jelikož v této měně lze na trhu nalézt širokou škálu investičních příležitostí (fondy vázané na jednotlivé indexy či US Treasury bonds.

Model se pokusí prokázat na základě historických dat, že diverzifikované portfolio nabízí v dlouhodobém horizontu vyšší výnos při nižší míře rizika než portfolio nediverzifikované.

Metoda

K simulaci je zvolena metoda Monte Carlo a nástrojem je MS Excel 2007. Tento postup se jeví jako vhodný, jelikož při stanovení dostatečně velkého množství iterací bude získáno mnoho potenciálních hodnot portfolia k bližší statistické analýze. Metoda Monte Carlo je velmi závislá na kvalitě zvoleného modelu a jeho zjednodušujících předpokladech. Zde použitý model však čerpá z historických dat a exaktních matematických a statistických postupů a za předpokladu, že na finančních trzích nedojde k převratným změnám, poté poskytne věrohodné výsledky.

Model

Parametry a omezení modelu

• pasivní přístup k portfoliu, poměr portfolia 75-25 (dynamícká a konzervativní složka),
• zvolená aktiva - S&P 500, Dow Jones Industrial Average, NASDAQ Composite, zlato a 30-year US Treasury bonds,
• délka investice - 30 let (na základě počtu let do důchodu),
• počáteční investice 5 000 USD, roční úložka 1 000 USD,
• historické hodnoty (z nichž se vypočítá potenciální výnos a směrodatná odchylka),
• normální rozdělení pravděpodobnosti, pravděpodobnost je daná vygenerovanou náhodnou hodnotou,
• předpokládá se, že na finančních trzích nedojde k převratným změnám,
• zjednodušený model abstrahuje od poplatků, daní a jiných překážek spojených s investováním.

Popis modelu

Model předpokládá počáteční investici ve výši 5000 USD s následnými ročními úložkami ve výši 1000 USD ročně, které jsou vkládány koncem roku, takže se daný rok neúročí. Doba odchodu do důchodu byla stanovena na 30 let, jelikož okolo 40. roku života začíná průměrný občan intenzivněji spořit na důchod, jehož hranice je okolo 70 let.

*výchozí hodnoty modelu (částky, které je investor schopen investovat a celková doba investování)

Numerická data pro analýzu historického vývoje byla získána z volně přístupné datové platformy Quandl. Zde byly získány třicetileté časové řady closingových hodnot indexu S&P 500, Dow Jones Industrial Average a NASDAQ Composite. Jako komodita bylo do portfolia zvoleno zlato a jeho časové řady získány tamtéž. Dluhopisem byl zvolen americký třicetiletý US Treasury Bond, časové řady získány také z Quandl.

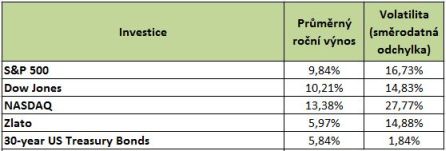
Z časových řad byl porovnáním s předcházejícím obdobím ((t0-t1)/t1) pro každý rok vypočten výnos, u dluhopisů byly výnosy již vlastním obsahem časové řady a nic dopočítávat nebylo třeba. Tyto vypočtené roční výnosové míry byly dále zprůměrovány a byla vypočtena směrodatná odchylka, která je velmi důležitým indikátorem volatility, tedy rizikovosti, portfolia.

=PRŮMĚR('S&P 500 - data'!G2:G31)

=SMODCH('S&P 500 - data'!G2:G31)         //kde G2:G31 je výčet hodnot S&P 500 vypočtených jako (t0-t1)/t1

*zvolené investice, vypočtený průměrný ročních výnos a volatilita jednotlivých investic

Z průměrného ročního výnosu a směrodatné odchylky je pro každé aktivum vypočteno 30 náhodně vygenerovaných výnosových měr. Zde je možno zcela bezpečně předpokládat normální rozdělení pravděpodobnosti, do vzorce pro výpočet potenciálního ročního výnosu je proto použita funkce inverzní k normálnímu rozdělení s následujícími parametry:

=NORMINV(pravděpodobnost, průměr, směrodatná odchylka)

Jelikož pravděpodobnost není známa, vygeneruje se náhodná hodnota funkcí NÁHČÍSLO(). Tímto postupem se získá pro každé aktivum 30 potenciálních ročních výnosových měr.

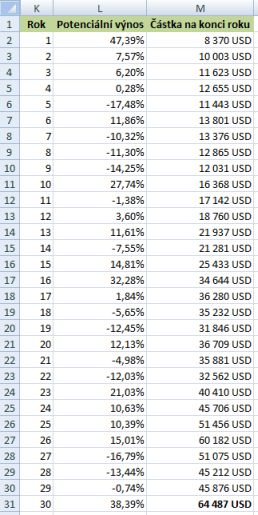
Následně jsou již zapojeny i finanční toky. Na základě výše zmíněných vygenerovaných výnosových měr je získána určitá hodnota portfolia na konci každého roku. Předpokládá se reinvestice všech zúročených prostředků. První rok se uloží 5000 USD, ty se zhodnotí a na konci přiloží 1000 USD. Druhý rok se výnosovou měrou vygenerovanou pro druhý rok zhodnotí konečná hodnota portfolia na konci prvního roku a opět se přidá 1000 USD, takto se postupuje až se získá hodnota portfolia po 30 letech.

=5000*(1+L2)+1000         //kde L2 je potenciální výnos investice

=M2*(1+L3)+1000           //kde M2 je částka na konci roku, L3 potenciální výnos investice

Níže příklad pro S&P 500.

*příklad vypočteného S&P 500

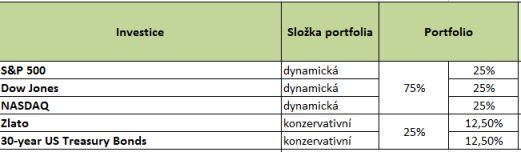
Tato konečná hodnota portfolia po 30 letech představuje jednu iteraci (za použití 30 jiných výnosových měr vypočítaných při průměrném historickém výnosu, směrodatné odchylce a náhodné pravděpodobnosti), těch je provedeno v excelu pro každé aktivum 30 000 za použití tabulek hodnot. Takto získaná data se následně podrobí statistické analýze. Vypočte se průměrná hodnota portfolia, medián, 10% a 5% percentil. Model se v konečné fázi zaměří na sestavení vhodného portfolia. Jednotlivé složky se rozdělí dle obecných doporučení investičních profesionálů takto:

*rozdělené portfolio na dynamickou a konzervativní složku na základě doporučené kombinace 75-25

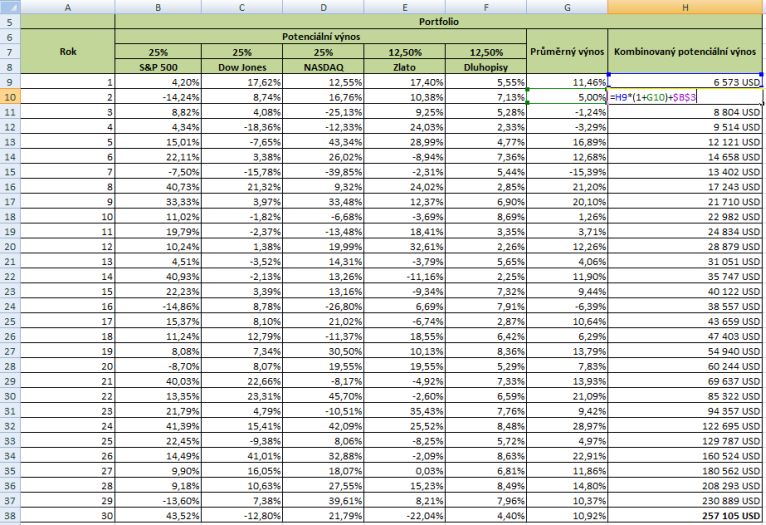
Indexy tvoří dynamickou složku, zlato a dluhopisy konzervativní část. Jsou rozděleny v poměru 75 % ku 25 %. Vypočte se 30 ročních hodnot takto kombinovaného portfolia tak, že se použije potenciální výnosové míry vygenerované pomocí již vypočtené funkce NORMINV a vynásobí se výnosovou míru každého aktiva jeho poměrem v portfoliu.

*vypočtené průměrné výnosy 30 ročních hodnot na základě doporučeného poměru portfolia

Pomocí vypočítaných výnosových měr se určí konečná hodnota portfolia po 30 letech stejným způsobem, jak ukázáno výše na příkladu S&P 500 a provede se 30 000 iterací tohoto výsledku.

Výpočet průměrné hodnoty portfolia, medián, 5% a 10% percentil:

=PRŮMĚR('S&P 500 - data'!L34:L30033)               //průměr z analýzy dat

=MEDIAN('S&P 500 - data'!L34:L30033)               //medián z analýzy dat

=PERCENTIL('S&P 500 - data'!L34:$L$30033;0,1)      //10% percentil z analýzy dat

=PERCENTIL('S&P 500 - data'!L34:$L$30033;0,05)     //5% percentil z analýzy dat

Nyní je k dispozici veškerá datová základna pro analýzu výsledků.

Výsledky

Výše popsaný model po provedení všech iterací vypočítal například tuto sadu výsledků (mírně se liší při každém přepočítání hodnot):

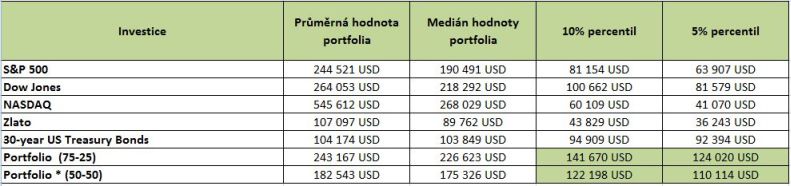
*příklad sady získaných výsledků (průměrná hodnota, medián, 5% a 10% percentil)

Průměrná hodnota portfolia je nejvyšší u investice pouze do NASDAQ a velmi nízká u dluhopisů a zlata. Tato veličina však není příliš vhodným indikátorem, jelikož průměr je ovlivněn do velké míry krajními hodnotami. Proto je vhodnějším ukazatelem medián (50% percentil), který řadu hodnot portfolia po 30 letech seřadí od nejnižšího po nejvyšší a určí střední hodnotu, která tuto řadu rozděluje na dvě stejně četné poloviny. Medián je opět nejvyšší u NASDAQ a nejnižší u zlata a dluhopisů. Jelikož se průměrné hodnoty portfolia značně liší od mediánu, můžeme usuzovat na značnou šikmost tohoto rozdělení. Klíčovým ukazatelem pro nás však budou nižší percentily, konkrétně 10% a 5% percentil. Ty nám říkají, že máme 90%, respektive 95% šanci získat konečnou hodnotu portfolia vyšší, než je výsledek v tabulce.

Portfolio:

Rozdělení složek portfolia je v poměru 75 % dynamická složka (indexy) a 25 % konzervativní složka (zlato a dluhopisy). Oba percentily mají vždy mnohem vyšší hodnotu, než u jednotlivých aktiv separátně. To znamená, že je možné očekávat při stejné procentní šanci (zde 90 % respektive 95 %) vyšší konečnou hodnotu portfolia po 30 letech u diverzifikovaného portfolia oproti portfoliu složenému z jednoho aktiva. Tato skutečnost byla potvrzena několikanásobným přepočtením všech iterací v modelu.

Portfolio*:

Rozdělení složek portfolia je v poměru 50 % dynamická složka (indexy) a 50 % konzervativní složka (zlato a dluhopisy). Opět se ukazuje, že je možno s vysokou mírou pravděpodobnosti očekávat vyšší výnos v dlouhodobém horizontu u takto diverzifikovaného portfolia, než u separátní investice do jednotlivých aktiv. Výsledky také ukazují, že doporučený model rozdělení 75-25 přináší šanci na vyšší míru zhodnocení, než model 50-50 za použití historických dat.

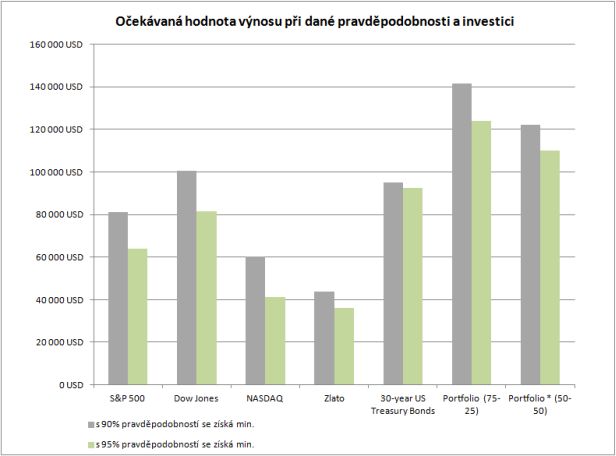
*příklad sady získaných výsledků při dané pravděpodobnosti a investici

Závěr

Model a jeho výsledky prokazují na bázi historických dat teorii diverzifikovaného portfolia, které při vhodném rozdělení investice do aktiv rizikových a konzervativních, přináší vyšší výnos v dlouhodobém horizontu než investice do jednotlivých aktiv. Ve výše uvedeném případě máme např. u portfolia s klasickým rozdělením rizikové a umírněné složky 75-25 95% šanci na získání nejméně 124 020 USD, přičemž nejbližší hodnotou jednotlivého aktiva je 95% šance na získání nejméně 92 394 USD při investici do třicetiletých amerických Treasury bonds. Částka okolo 100 000 USD pravděpodobně zajistí průměrnému investorovi dostatečnou stabilitu v důchodu.

Kód

File:Simulace Xkrep00.xlsx