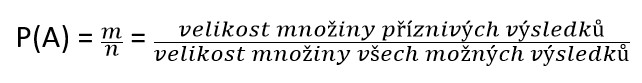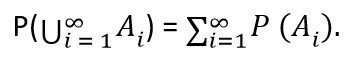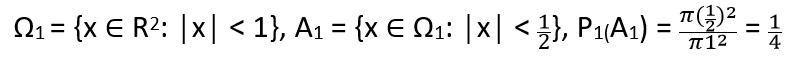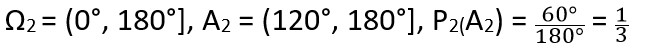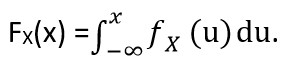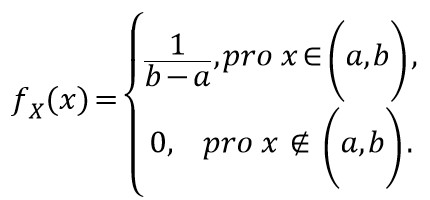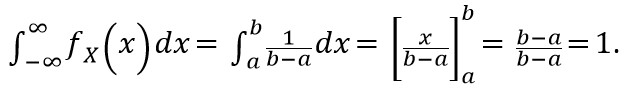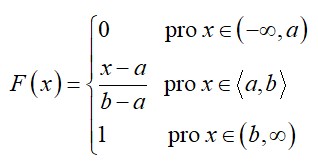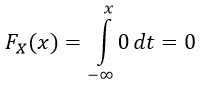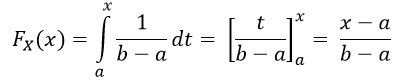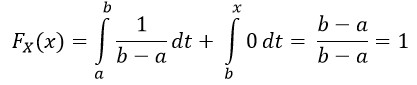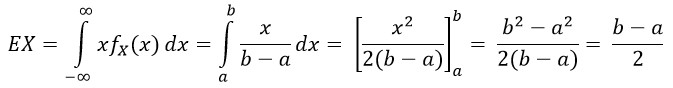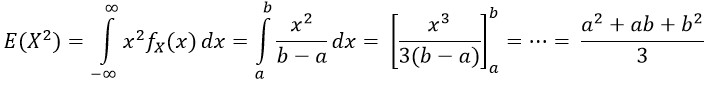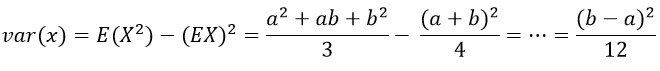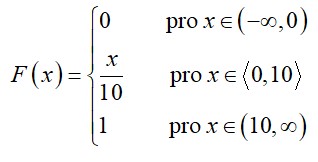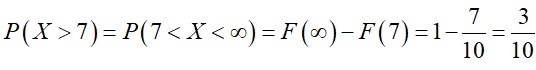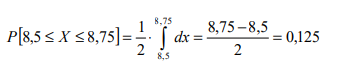Rovnoměrné rozdělení (česky)

V běžném životě se setkáváme s procesy, u kterých není snadné předem určit, jak dopadnou. Pokud se tento problém převede do světa matematiky, tak se jedná o jevy, u kterých nejsme schopni předem s jistotou určit, jaký z možných výsledků nastane. Takto predikovat výsledek není často možné z důvodu, že je sledovaný jev příliš složitý a komplexní, nebo o něm nejsou známy všechny potřebné informace, tj. jeho výsledek je určen nějakou náhodou. Pro lepší představu je možné si pod těmito jevy představit různé experimenty, testy, přírodní jevy apod.

Touto problematikou se zabývá teorie pravděpodobnosti. Ta se snaží tuto náhodu určit matematicky. Výsledkům pokusů přiřazuje jejich pravděpodobnost, která udává podíl případů, kdy nastane daný výsledek. Na základě těchto jednoduchých modelů je pak možné řešit složitější problémy.

Například: Máme k dispozici vyváženou (nebo také spravedlivou) minci. Za pomoci této mince můžeme spočítat, jaká je pravděpodobnost, že nám z 2000 hodů padne 100 orlů. Zde je důležité specifikovat, že se jedná o vyváženou (nebo také spravedlivou) minci. Kdyby nebyla mince vyvážená, padala by panna nebo orel častěji a tento experiment by tím byl značně zkreslen.

Termilonogie

Veškeré popsané definice by měly být popsány v kapitole Opáčko ze statistiky: Pravděpodobností rozdělení nebo Pravděpodobnostní rozdělení. Jelikož je opakování matka moudrosti, budou zde v krátkosti popsány základní definice z teorie pravděpodobnosti, které nejsou stoprocentně pokryty ve výše zmíněných kapitolách.

Experiment, pravděpodobnostní prostor a náhodný jev

Na začátku je třeba matematicky definovat, co znamená jev a experiment. Jev je možné popsat jako množinu, které se bude přiřazovat pravděpodobnost. Experiment je poté definován jako pravděpodobnostní prostor, který je určen jako trojice:

ε = (Ω, Ϝ, Ρ),

kde Ω obsahuje všechny výsledky určitého experimentu, Ϝ označuje kolekci všech možných jevů, kterým je možné přiřadit pravděpodobnost P.

Náhodný jev A je možné chápat jako množinu elementárních jevů, tedy nějakou podmnožinu A z množiny Ω.

Například: Hod dvěma vyváženými mincemi – množinově vyjádřený jev, že padne alespoň jednou panna P (orel značen O). Prostor elementárních jevů je Ω = {(P, P), (P, O), (O, P), (O, O)}. Sledovaný jev A tedy bude: A = {(P, P), (P, O), (O, P)} tj. podmnožina množiny Ω.

Pro takto množinově definovaný jev je možné používat množinové operace jako je sjednocení a průnik dvou a více množin nebo opačný jev k jevu A.

Klasická definice pravděpodobnosti

Za klasickou definici pravděpodobnosti je možné považovat tu, kterou zformoval francouzský matematik Pierre-Simon Laplace na přelomu 18. století a je definována takto:

P(A) značí pravděpodobnost sledovaného jevu A (například zmíněný hod mincí), která je rovna podílu příznivých výsledků a všech možných výsledků. Definice předpokládá, že se jedná o konečný počet výsledků několika vzájemně různých pokusů, které jsou všechny stejně pravděpodobné (viz poznámka o vyvážené minci).

Například: Pozorovaný jev A je hod vyváženou mincí. Zajímá nás, jaká je pravděpodobnost, že padne orel? Mince má dvě strany, na jedné je panna a na druhé orel. Všechny možné výsledky jsou 2 a nás zajímá pouze orel. Výsledkem je tedy 0,5, tj. 50% šance, že padne orel.

Jelikož je možné vyjádřit pravděpodobnost procenty, je její hodnota v rozmezí mezi 0 % a 100 %, to jest výsledek podílu výše je mezi 0 a 1 a současně platí, že je maximálně 1. Toto vychází z definice pravděpodobností míry (viz kapitola níže). Toto je možné jednoduše vysvětlit na příkladu s vyváženou mincí.

Pravděpodobnost, že padne orel, je stejná jako, že padne panna. Toto jsou jediné dva výsledky, které mohou nastat. Pokud sečtu pravděpodobnosti všech možných výsledků, dostanu hodnotu 1 (0,5 + 0,5 = 1).

Vedle této klasické definice pravděpodobnosti, je možné v jiných textech nalézt jiné definice (například dle A. N. Kolmogorova, axiomatickou, statistickou či geometrickou). Pro jednodušší vysvětlení rovnoměrného rozdělení je zde uvedena ještě jedna definice a to grafická.

Grafická definice pravděpodobnosti

Grafická definice pravděpodobnosti nahlíží na sledovaný jev A z hlediska jeho relativní velikosti. Předpokládá, že výsledky tohoto jevu nastávají v nějakém geometrickém objektu či množině o konečné velikosti (například plochy, délky, objemu, apod.), kde je každý tento výsledek stejně pravděpodobný. Pravděpodobnost tohoto jevu A je poté definována takto:

Stejně jako je napsáno u klasické definice pravděpodobnosti, je analogicky odůvodnitelné, že součet pravděpodobností všech výsledků je 1, tj. maximální velikost množiny (plochy) je 1.

Například: Romeo a Julie se mají setkat na tajném místě mezi polednem a 1 hodinou odpoledne. Každý z nich dorazí v náhodném okamžiku v tomto určeném čase a počká zde pouze 15 minut. Pokud ten druhý nedorazí, odejde. Jaká je pravděpodobnost, že se potkají?

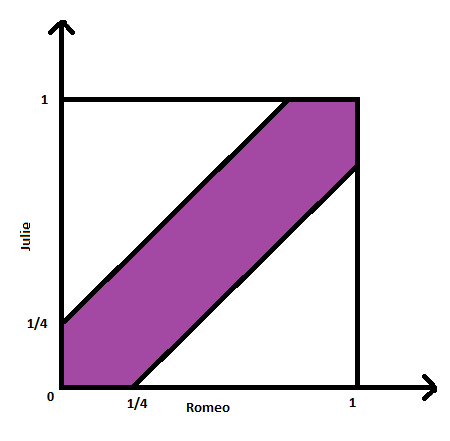
Celková plocha je 1. Vybarvená oblast odpovídá situacím, kdy se setkají. Pravděpodobnost, že se potkají je následující:

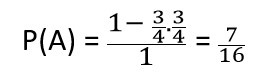
Pro určení výsledku byla použita pravděpodobnost opačného jevu a nezávislosti dvou pozorovaných jevů.

Pravděpodobnostní míra

Pravděpodobnostní míra na (Ω, Ϝ) je funkce P: F → R (F je zobrazení na množinu reálných čísel) splňující:

    1) nezápornost: pro každé A ∈ F platí P(A) ≥ 0,

    2) normalizace: P(Ω) = 1,

    3) σ – aditivita: když jsou A₁, A₂ … ∈ F vzájemně disjunktní jevy (A_i ∩ A_j = ∅ pro ∀i, j: i ≠ j), tak

 

Z této definice plyne, že pro každé A ∈ F platí 0 ≤ P(A) ≤ 1. Jak již bylo zmíněno výše, pravděpodobnost je možné uvádět v procentech tj. 0 % až 100 %. Je nutné správně definovat volbu P a to, co je myšleno pod pojmem „náhodný“. Vágně zadaný příklad může vést k paradoxům.

Například: Bertrandův paradox – Náhodná tětiva X na jednotkové kružnici. Jaká je pravděpodobnost P(A), kde A = {│x│ > l} a l je strana libovolného vepsaného rovnostranného trojúhelníku? Zde záleží na tom, co je míněno pod slovem „náhodná“:

    1) Vybereme rovnoměrně náhodně střed x:

    2) Vybereme rovnoměrně náhodně úhlovou velikost a směr tětivy x viděné ze středu:

  

    3) Vybereme rovnoměrně náhodně vzdálenost tětivy x od středu a směr:

   

Náhodné veličiny

Výsledkem náhodného experimentu často nebývá číslo. Aby bylo možné takové experimenty matematicky zpracovat, je vhodné každému výsledku přiřadit jeho číselnou hodnotu. Vhodným přiřazením je výběr informace, která je pro nás zajímavá. Toto přiřazení je možné provést několika způsoby, proto je nazýváno náhodnou veličinou a značí se X, Y, apod.

Například: Počítání orlů při hodu vyváženou mincí: X(orel) = 1, X(panna) = 0. Toto přiřazení je vyobrazené na obrázku níže.

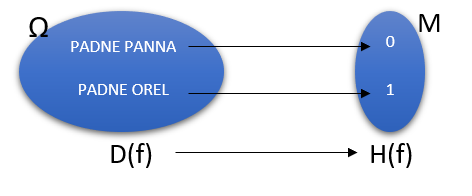
Matematicky je definice stanovená takto: Náhodná veličina X na pravděpodobnostním prostoru (Ω, F, P) je funkce, která každému výsledku experimentu ω ∈ Ω přiřadí hodnotu X(ω) ∈ R a pro kterou platí podmínka měřitelnosti:

{X ≤ x} ∈ F pro všechna x ∈ R.

Podmínka měřitelnosti říká, že {X ≤ x} je náhodný jev, u kterého je možné spočítat jeho pravděpodobnost.

Distribuční funkce

Distribuční funkce určuje pravděpodobnost, že náhodná veličina nabude hodnoty menší než x případně hodnoty x. Lze ji formálně definovat takto: Funkci F_X : R → R definovanou vztahem F_X(x) = P(X ≤ x) nazýváme distribuční funkcí náhodné veličiny X.

Základními vlastnostmi distribuční funkce jsou, že nabývá hodnot z intervalu, je neklesající, je zprava spojitá (zde záleží na konkrétní definici, může být spojitá zleva) a má nejvýše spočetně mnoho bodů nespojitosti.

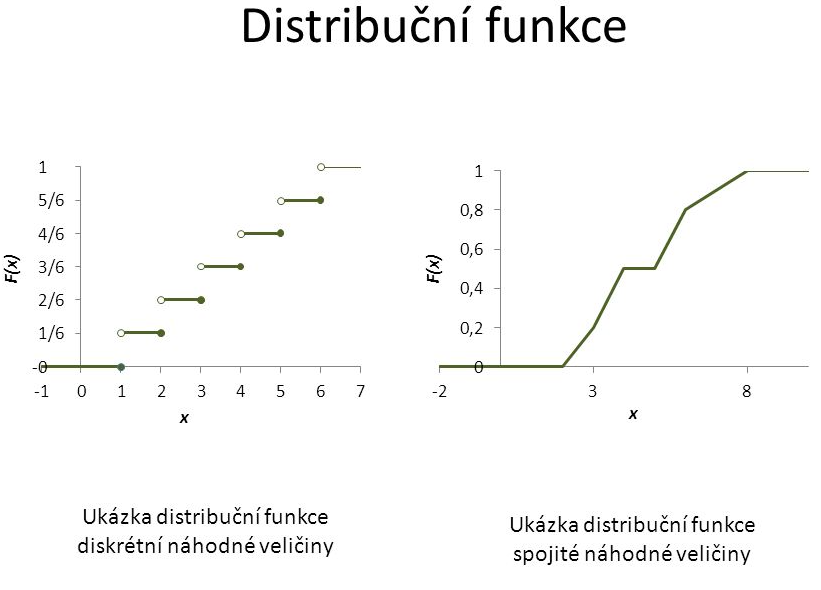
Hustota pravděpodobnosti

Protože v některých případech nabývá náhodná veličina nespočetně mnoha hodnot (například měření času, vzdálenosti, apod.), není možné přiřadit kladnou pravděpodobnost P(X = x) každé hodnotě, protože by se nespočetné množství takových pravděpodobností nasčítalo na nekonečno. Proto je každé jednotlivé hodnotě přisouzena nulová pravděpodobnost. Je třeba měřit pravděpodobnost intervalů. Intuitivně je zřejmé, že pravděpodobnost, že budu čekat na tramvaj nebo autobus přesně 3 minuty je nulová. Hustotu pravděpodobnosti f(x) spojité náhodné veličiny je možné popsat jako reálnou nezápornou funkci takovou, že ve všech bodech, kde existuje derivace distribuční funkce platí, že plocha pod křivkou hustoty pravděpodobnosti je rovna 1.

Další důležité pojmy

Další důležité pojmy jako střední hodnota, rozptyl a kvantily jsou popsány v kapitole Opáčko ze statistiky: Pravděpodobností rozdělení nebo Pravděpodobnostní rozdělení..

Pravděpodobnostní rozdělení

Pravděpodobnostní rozdělení nebo rozložení náhodné proměnné udává, jaká je pravděpodobnost, že náhodná veličina bude mít zrovna danou hodnotu. Náhodné veličiny dělíme na diskrétní a spojité. Diskrétní náhodná veličina nabývá jednotlivých hodnot jako například 0 jako panna nebo 1 jako orel při hodu mincí nebo hodnoty 1 až 6 při hodu kostkou. Spojité nabývají hodnot na spojité škále, tj. nějaké intervaly. Příkladem může být váha novorozence, doba čekání na autobus, apod.

Diskrétní rozdělení

Náhodné veličiny X se nazývají diskrétní, pokud nabývají pouze hodnot z nějaké nejvýše spočetné množiny {x₁, x₂, x₃ … x_k}, kde k = 1, 2, 3, 4, … n ∈ N. Pravděpodobnosti možných hodnot náhodné veličiny X jsou P(X = x_k), kde k = 1, 2, 3, 4, … n ∈ N. Tuto pravděpodobnost P(X = x_k) je možné chápat jako funkci x, kterou je možné nazvat pravděpodobnostní funkcí nebo diskrétní hustotou náhodné veličiny X. Nenulovou pravděpodobnost mají pouze ty hodnoty x_k, kterých náhodná veličina X nabývá.

Mezi nejznámější příklady diskrétních náhodných veličin jsou:

    1) Bernoulliho (nebo také Alternativní) rozdělení

    2) Binomické rozdělení

    3) Geometrické rozdělení

    4) Poissonovo rozdělení

Spojitá rozdělení

Náhodné veličiny X se nazývají spojité, pokud existuje nezáporná funkce f_X taková, že pro každé x ∈ R můžeme vyjádřit distribuční funkci F_X jako

Funkci f_X v takovémto případě odpovídá hustotě pravděpodobnosti náhodně veličiny.

Mezi nejznámější příklady spojitých náhodných veličin jsou:

    1) Rovnoměrné rozdělení

    2) Exponenciální rozdělení

    3) Normální rozdělení

    4) Logaritmicko-normální rozdělení

    5) Cauchyovo rozdělení

    6) Studentovo t-rozdělení

Rovnoměrné rozdělení

Rovnoměrné rozdělení je jedno z nejjednodušších rozdělení. Toto rozdělení má pro všechny hodnoty náhodné veličiny stejnou pravděpodobnost. Může být zaraženo, jak mezi diskrétními, tak i spojitými náhodnými veličinami.

Diskrétní rovnoměrné rozdělení

Toto rozdělení popisuje náhodnou veličinu, která může nabývat n různých hodnot, které mají stejnou pravděpodobnost Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{1}{n}} . Předpokládá se, že vzdálenost mezi těmito hodnotami náhodné veličiny je stejná. Toto rozdělení představuje jedno z nejjednodušších případů diskrétního rozdělení.

Typickým příkladem diskrétního rovnoměrného rozdělení je hod šestistěnnou hrací kostkou, kdy pravděpodobnost padnutí každého z čísel je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{1}{6}} .

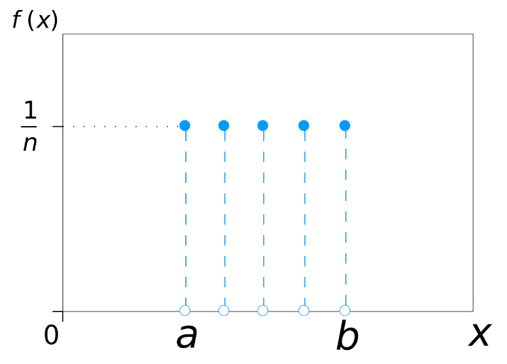
Tato kapitola se dále věnuje spojitému rovnoměrnému rozdělení.

Spojité rovnoměrné rozdělení

Rovnoměrné rozdělení, které se značí X ∼ U(a,b), má dva parametry – a jako minimální hodnotu a b jako maximální hodnotu, kde a a b jsou z intervalu −∞ < a < b < ∞.

Definice

Náhodná veličina X má rovnoměrné (uniformní) rozdělení na intervalu (a,b), kde a < b, pokud je její hustota pravděpodobnosti na tomto intervalu konstantní. Je vyjádřena vztahem:

Takto vypadá graf hustoty pravděpodobnosti spojitého rovnoměrného rozdělení:

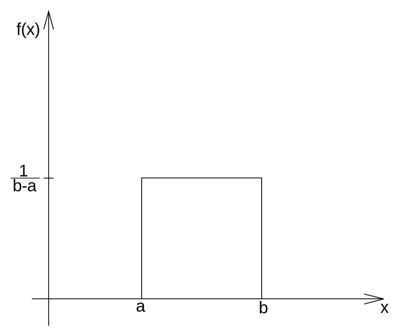
Vlastnosti

Jednou z vlastností tohoto rozdělení je, že hodnota plochy pod grafem hustoty je 1. Mimo daný interval (a, b) je tedy hustota pravděpodobnosti nulová. Toto je možné snadno ověřit:

Distribuční funkce rovnoměrného rozdělení je následující:

Takto vypadá graf distribuční funkce spojitého rovnoměrného rozdělení:

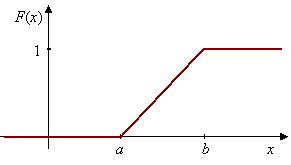
Vyjádření distribuční funkce lze snadno odvodit ze základní vlastnosti distribuční funkce a hustoty pravděpodobnosti:

    1) pro x ∈ (-∞, a):

 

    2) pro x ∈ [a, b]:

 

    3) pro x ∈ (b, ∞):

 

Střední hodnotu (aritmetický průměr) EX je možné odvodit následovně:

 

Rozptyl je průměrem druhých mocnin odchylek jednotlivých hodnot od aritmetického průměru z hodnot statistického souboru. Je možné ho zapsat vzorcem var X = E(X²) – (EX)². Pro odvození rozptylu, je třeba nejdříve zjistit E(X²):

 

Ze střední hodnoty X² je možné odvodit rozptyl následovně:

 

Souhrn všech důležitých vlastností a vzorečků

 

Řešené příklady

Příklad 1: Tramvajová linka číslo 8 odjíždí v dopoledních hodinách ze zastávky každých 10 minut. Vypočtěte pravděpodobnost, že na ni budete dopoledne čekat déle než 7 minut.

Řešení: Doba čekání je náhodná veličina X, která má rovnoměrné rozdělení pravděpodobnosti - v tomto případě X ∼ U(0, 10). Distribuční funkce má tedy tvar:

Hledaná pravděpodobnost:

Příklad 2: Prodejna očekává dodávku nového zboží určitý den v době od 8 do 10 hodin. Podle sdělení dodavatele je uskutečnění dodávky stejně možné kdykoliv během tohoto časového intervalu. Jaká je pravděpodobnost, že zboží bude dodáno v době od půl deváté do tři čtvrtě na devět?

Řešení: X ∼ U(8, 10).

Reálné aplikace

Jelikož je pravděpodobnost rovnoměrného rozdělení snadno vypočitatelná, existuje tedy řada dalších aplikací, pro které lze toto rozdělení použít, jak je uvedeno níže, je ho možné využít pro situace při testování hypotéz, případy náhodného vzorkování, finance, atd. Dále obecně platí, že pro experimenty fyzikálního původu, je možné taktéž využít rovnoměrného rozdělení (např. emise radioaktivních částic).

Dále je toto rozdělení možné použít také pro příklady typu doba čekání do nastoupení určitého jevu, který se opakuje v pravidelných intervalech, nebo chyby při zaokrouhlování v numerických výpočtech. Zaokrouhlují-li se čísla na k desetinných míst, lze chybu ze zaokrouhlování považovat za náhodnou veličinu s rovnoměrným rozdělením na intervalu <-5.10^-k-1; 5.10^-k-1>.

Ekonomický příklad

V oblasti ekonomiky nemusí poptávka a doplňování zboží obvykle odpovídat očekávanému normálnímu rozdělení. Výsledkem je, že se k lepší předpovědi pravděpodobností a trendů používají jiné distribuční modely, jako je Bernoulliho proces. V případě zkoumání doby pro správu zásob na začátku, kdy se analyzuje zcela nový produkt, se ukazuje jako užitečnější rovnoměrné rozdělení. V této situaci nemusí být jiné rozdělení použitelné, protože o novém produktu neexistují žádná stávající data nebo není k dispozici historie poptávky, takže ve skutečnosti neexistuje vhodné nebo známé rozdělení. (Rovnoměrné rozdělení by bylo v této situaci ideální, protože náhodná proměnná, která souvisí s poptávkou, není u nového produktu známa, ale výsledky se pravděpodobně budou pohybovat mezi přijatelným rozsahem dvou hodnot.) Toto by tedy představovalo vhodnou náhodnou proměnnou. Z modelu rovnoměrného rozdělení je možné vypočítat další faktory související s dobou realizace. Další výhodou použití rovnoměrného rozdělení je jeho jednoduchost.

Chyba kvantování

Při analogově-číslicovém převodu dojde k chybě kvantování. Tato chyba je způsobena zaokrouhlením nebo zkrácením. Když je původní signál mnohem větší než jeden nejméně významný bit (LSB), chyba kvantování významně nekoreluje se signálem a má přibližně rovnoměrné rozdělení. Chyba RMS tedy vyplývá z rozptylu této distribuce.

Funkce v Excelu

V excelu pro toto rozdělení není funkce, která by šla použít přímo.

Příklady pro studenty k procvičení

Příklad 1: Náhodná veličina X má rovnoměrné rozdělení. Jaká je její hustota, jestliže EX = 1, var X = 3?

Příklad 2: Dělník obsluhuje v dílně 4 stroje. U prvního stroje stráví 10 minut, u druhého 25 minut, u třetího 15 minut a u čtvrtého 10 minut, poté se opět vrací k prvnímu stroji. Určete pravděpodobnost, že přijdeme-li do dílny v náhodný okamžik, zastihneme ho u třetího stroje.