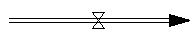Stock and Flow Diagram/cs
Contents
Diagram toků (SFD)
Pro zobrazení systémové dynamiky do modelu můžeme použít dva druhy diagramů – Loop Diagram (příčinný smyčkový diagram nebo také diagram kauzálních smyček) a Stock and Flow Diagram (diagram stavů a toků). Oba modely slouží k zachycení zpětnovazební struktury systému, avšak mezi těmito druhy diagramů jsou velké rozdíly.
| I když je tvoření modelu úplným základem systémové dynamiky, zatím neexistuje žádná metodologie pro tvorbu modelů systémové dynamiky. Mnoho zdrojů pouze postupy tvorby modelů DOPORUČUJE. [volný překlad, zdroj [1], str 24 |
Rozdíly mezi SFD a CLD
Loop Diagram (CLD) slouží k zobrazování zpětných vazeb (pozitivních a negativních). CLD může sloužit vlastně jako takový „podklad“ pro tvorbu SFD. Ačkoliv je docela úsměvné, že SFD se nevyvinul z CLD, ale CLD z SFD. CLD vzniklo hlavně proto, aby přístupy systémové dynamiky (do „vzniku“ CLD byla systémová dynamika oblastí spíše jenom pro inženýry) byly více a snáze pochopitelné pro širokou veřejnost.
| Fun fact – v literatuře od českých autorů dochází k zajímavým dezinformacím. Zdroj [1, volný překlad] uvádí, že „Z historického pohledu vývoje dynamiky systémové metodologie CLD byl vytvořen dříve než SFD“, načež v Zdroj [2]: „Z historického pohledu vývoje systémově dynamické metodologie je příčinný smyčkový diagram (CLD) mladší než diagram hladin a toků (SFD)“. Pravděpodobně je Zdroj [1] špatně přeložen z češtiny do angličtiny. Zdroj [4]: “The first system dynamics work did not include the use of causal-loop diagrams. Feedback structure was portrayed by equations or stock-and-flow diagrams. Such representations were natural for engineers. In an attempt to make system dynamics accessible to a wider range of people, causal-loop diagrams have become increasingly popular“. |
CLD má mnoho výhod i nedostatků oproti SFD. CLD znázorňuje jednoduchou formulaci problému, rychle se vytvoří, snadno pochopí (viz Tabulka 1), avšak umí jenom znázornit, co by se stalo, kdyby došlo ke změně v systému (skrz plus a mínus). A hlavně, nedokáže rozlišit toky a informace, což se v případě SFD promítlo rovnou do názvu diagramu: „Diagram stavů a toků“.
| Kritérium\Diagram | Diagram hladin a toků (SFD) | Příčinný smyčkový diagram (CLD) |
|---|---|---|
| Náročnost vytvoření diagramu | - | + |
| Původní přesnost modelářovy představy o struktuře systému | + | - |
| Specifičnost (detailnost popisu) | + | - |
| Snadnost pochopení | - | + |
Tabulka 1, Zdroj [2]
CLD je tedy vhodné používat:
1. Jako „předboj“ tvorby SFD.
2. Pokud chci jenom znázornit druhy zpětných vazeb (pozitivní a negativní) bez více podrobností.
3. Pokud chci udělat model, kterému bude rozumět i úplný laik. Tzn. Jako jednoduchý způsob popsání základná dynamiky vztahů v systému.
Jinak se pustíme do SFD.
Stock and Flow diagram
Ze stručného popisu CLD jsme už mohli zjistit, že SFD je prostě komplikovanější než CLD a jeho pochopení i tvorba zabere daleko více času. Jak už bylo řešeno, SFD neumí jenom zobrazit šipečky s plusky a mínusky (pozitivní a negativní zpětné vazby). Model dokáže odlišit hladiny a toky, což na první pohled vypadá jenom jako nejasná definice vytvářející problémy při závěrečném testu (tzn. komplikace při tvorbě modelu), avšak existují důvody, proč je to potřeba: „Rozlišováním stavových a tokových proměnných se vyhýbají interpretačním problémům, které mohou vznikat u příčinným smyčkových diagramů“ Zdroj [3].
Nejdříve si definitivně ujasníme, jaký je rozdíl mezi tokem a stavem, potom si dovysvětlíme zbylé stavební bloky SFD s grafickým znázorněním a poté vyzkoušíme na několika příkladech tvorbu SFD. V závěru se dočtete o několika radách při tvorbě modelu, případně tipy & triky jak úspěšně napsat závěrečný test 4IT495.
| V čem model vytvářet?
Na tvorbu modelů SFD se nejčastěji používají programy Powersim (www.powersim.com) nebo Vensim (vensim.com). PS. Na hodinách 4IT495 se model modeluje ve Vensimu, proto je k tomu uzpůsobený i tento studijní text. |
Stavy a toky
Stavy neboli úrovně, neboli hladiny, neboli akumulace, neboli stavové veličiny (výsledek nejasné metodologie systémové dynamiky, kdy si každý software pro tvorbu modelů používá svůj vlastní název):
- jsou akumulacemi změn za časový okamžik,
- zachycují stav systému,
- mohou být kdykoliv během simulace změřeny,
- jsou ovlivňovány toky směřujícími dovnitř i ven,
- jsou zdrojem zpoždění v systému,
- musí mít vždy počáteční hodnotu (číslo nebo proměnnou).
Stav je ovlivňován toky, tj. zobrazuje aktuální stav přítoků a odtoků, co dosud simulací prošly. Mohou být fyzické (zásoby na skladě) i abstraktní / nehmatatelné (vnímaná atraktivita produktu).
Příklady stavů:
- peníze na účtu
- zásoby na skladě
- objem nevyřízených objednávek
- kvalita produktu
- spokojenost zákazníka
- množství vody v přehradě
- množství mízy ve stromu
- množství plynu CO2 v atmosféře
- počet nájemních domů v Brně
- objem tuku v těle
- počet aut v městě
- počet návštěvníků zoo
- objem benzínu v nádrži
Toky neboli míry mění stavy. Toky jsou ovšem měněny právě změnami stavů (takové zacyklení). Jsou procesem, který naplňuje nebo vyprazdňuje stavy (hladiny), jeden tok může dělat zároveň obojí (jeden stav naplňovat, druhý vyprazdňovat). Toky vždy reprezentuje nějakou jednotku za určitý čas, viz následující příklady.
Příklad č.1:
Tok: množství vody přitékající kohoutkem (litrů / minutu)
Stav: množství vody ve vaně (litrů)
Odtok: množství vody odtékající odtokem (litrů / minutu)
Příklad č.2:
Tok: míra narozených dětí (narození / rok)
Stav: počet obyvatel (počet)
Odtok: míra úmrtí (úmrtí / rok)
Další příklady toků:
- příchod objednávek (objednávek / týden)
- snižování kvality
- vypouštění přehrady
- narození
- prodej aut (aut / měsíc)
- míra úmrtnosti
- prodej vakcín (počet prodaných vakcín / rok)
- výkon
- příjmy
Jak ještě odlišit stavy a toky:
Oproti všemu výše zmíněnému je potřeba zdůraznit jeden hlavní rozdíl. Pokud by se nám podařilo teoreticky zmrazit čas, stavům budou jejich hodnoty zachovány (neztratí se), avšak toky se ztratí, budou bez hodnoty. Což je například krásně vidět na příkladu vody ve vaně - když zmrazíme čas, v odtoku a v přítoku se nebude dít nic, nacházet nic, bez hodnoty. Za to vana bude obsahovat několik litrů vody.
Základní stavební bloky SFD
Když teď už chápeme rozdíly mezi stavy a toky, můžeme se vrhnout do modelů.
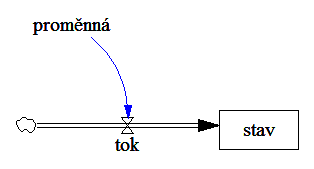
Příklad SFD modelu:
A jednotlivé části:
Proměnná (pomocná)
Označuje pomocnou informaci, konstantu, atd. Proměnné jsou ovlivňovány toky, stavy a jinými proměnnými, avšak samotné proměnné ovlivňují pouze toky nebo proměnné (ne stavy) anebo nemusí být ovlivňovány vůbec (např. konstanty).
Mrak
Mráček představuje hranice modelu, má nekonečnou kapacitu. Je to magický obsah, jenž nám pro potřeby modelu není znám. Znázorňuje zdroj a konec toků odehrávající se někde mimo model.
Spoj
Spoj je linie, kterou propojujeme vazby mezi proměnnými, toky a stavy. Po spojích putují informace dál (ve směru šipky), určují, co je čím ovlivňováno (avšak ne jak ovlivňováno).
Tzn. Když všechny tyto informace aplikujeme na výše zmíněné příklady:
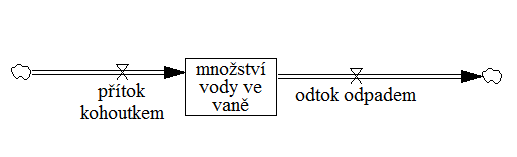
Příklad 1:
Tento model nám říká, že odněkud (mráček) přitéká voda kohoutkem (tok), jenž ovlivňuje množství vody ve vaně (stav) a odtéká odpadem pryč z modelu (druhý mráček).
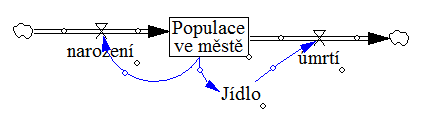
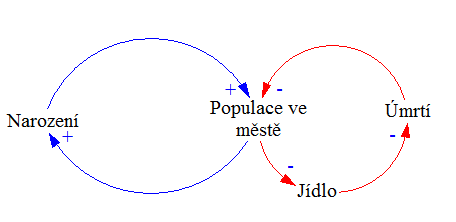
Příklad 2 (rozšířen o proměnnou Jídlo):
… jenž vychází z původního CLD:
Model CLD tedy říká, že počet narozených lidí pozitivně ovlivňuje počet obyvatel ve městě (a čím jejich více, tím větší je počet narozených lidí), avšak čím více je lidí, tím méně je jídla, tím více se umírá a tím menší je populace.
SFD říká svým modelem to stejné, avšak bez pozitivních a negativních informací, dokud nezadám parametry každé proměnné, toku a stavu.
| Ačkoliv to doteď tak mohlo vypadat, stavy nemusí vždy (přes toky) vycházet mimo systém a odcházet ze systému. Není to povinnost, stav už může být zadán v systému a ze systému ani neodcházet. |
Převedení CLD na SFD
Jsou tři věci, které si musíme při tvorbě modelu SFD na základě CLD důkladně promyslet:
1. Určit, co je tokem, co je stavem a co proměnnou.
2. Určit, kde jsou hranice modelu (kam dát správně, a pokud vůbec, mráčky).
3. Kvantifikovat jejich parametry (pokud nejsou už zadané).
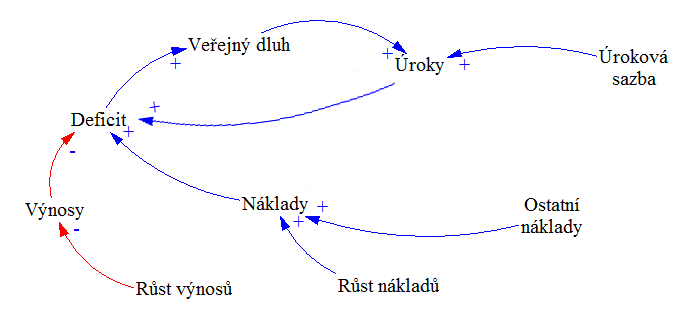
Mějme CLD:
Zdroj [6] – přeloženo do češtiny
A předěláme ho do SFD:
Z toho jsme se dozvěděli dvě věci:
1. Ne vše, co je zanesené v CLD stačí pro tvorbu SFD. CLD je velmi zjednodušený model znázorňující jen pozitivní a negativní vazby, zatímco SFD je daleko rozsáhlejší model a je potřeba přidat další informace (např. Zaplacené úroky).
2. Pokud bychom toto zadali například deseti lidem k vypracování, pravděpodobně se bude pár modelů trochu lišit (viz doplněné informace, co nebyly v CLD) anebo lišit přístupem k zadaným informacím.
| Spoje stavu
Do stavu nesmí mířit žádný spoj kromě toku. Avšak nemůže mít přímou vazbu například s proměnnou. Ze stavu už spoje můžou mířit |
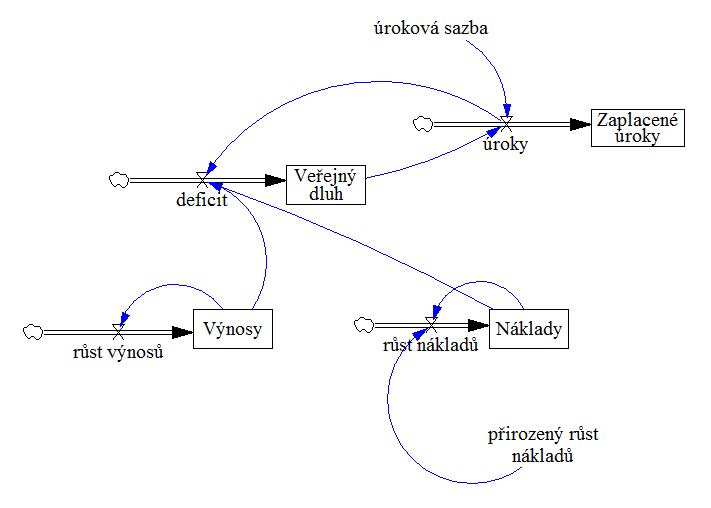
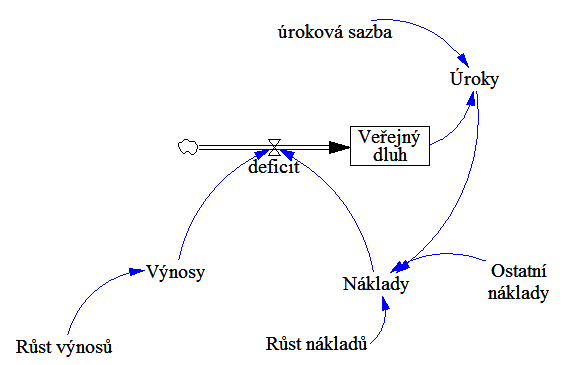
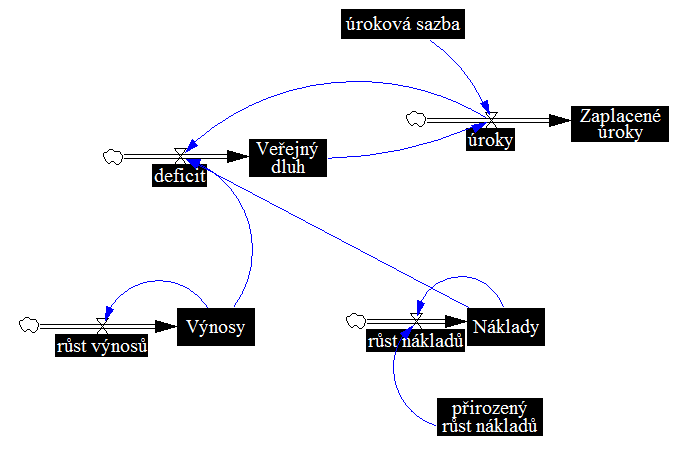
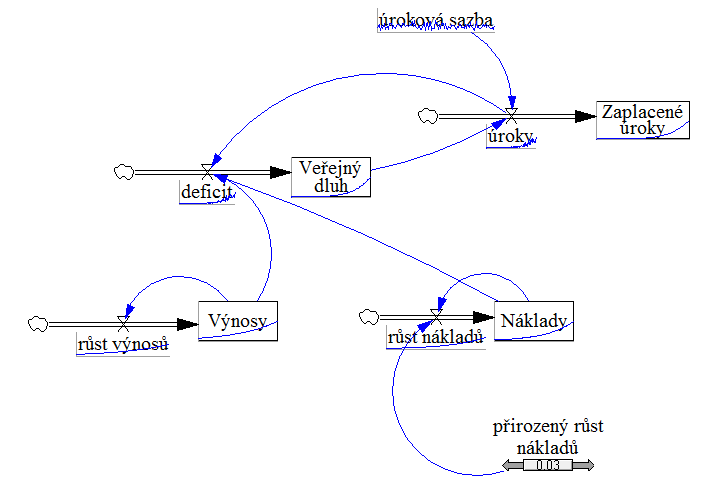
Tento stejný model SFD byl vypracován nejméně 2x a vždy se na něj nahlíželo jinak. V přednáškách předmětu 4IT495 (ke 2014) je vypracován takto, avšak na stránkách simulace.info je takto:
Druhý model je chybný (nehledě na vazbu Úroků a Nákladů), protože když hypoteticky zastavíme čas (zmrazíme), máme zde vyjádřený jen Veřejný dluh, avšak Výnosy a Náklady nebudou najednou obsahovat nic. V předchozím modelu, tedy správně vypracovaném, když zmrazíme čas, Veřejný dluh, Náklady, Výnosy i Zaplacené úroky budou mít hodnoty. A také na příkladu (v druhém modelu) Výnosů můžeme vidět, že takové Výnosy budou vždy stejné, protože neexistuje zpětná vazba Výnosů na Růst výnosů, jako je ve správném modelu.
Dále budu pracovat s vypracovaným modelem z přednášek (první model SFD).
Parametry SFD
Tento model nám tedy znázorňuje, co koho ovlivňuje, ale už ne JAK. V rámci modelu SFD jsou plusy a mínusy z CLD převedené do detailnějšího popisu skrz parametry jednotlivých objektů modelu. Celé zadání může vypadat takto:
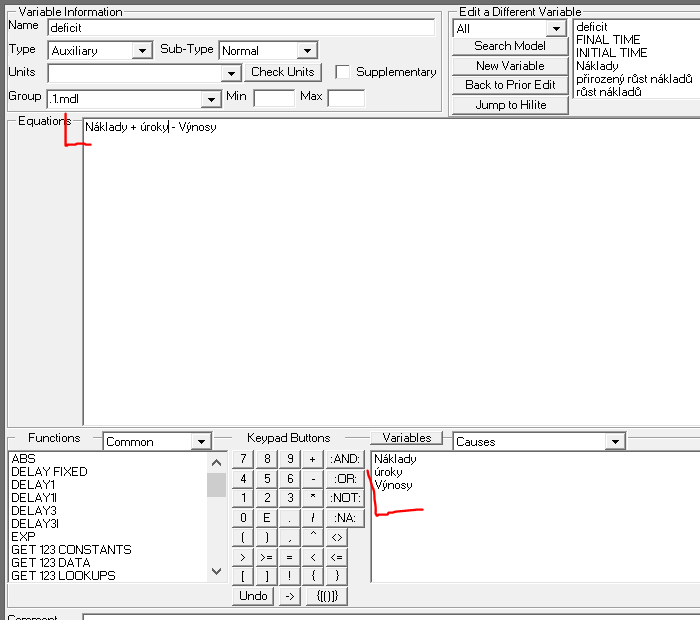
- Deficit = Náklady + Úroky - Výnosy
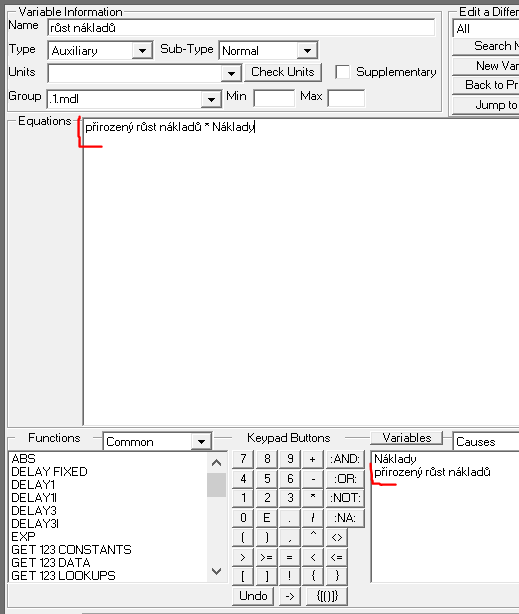
- růst nákladů = přirozený růst nákladů * Náklady
- Náklady = INTEG (růst nákladů, 610)
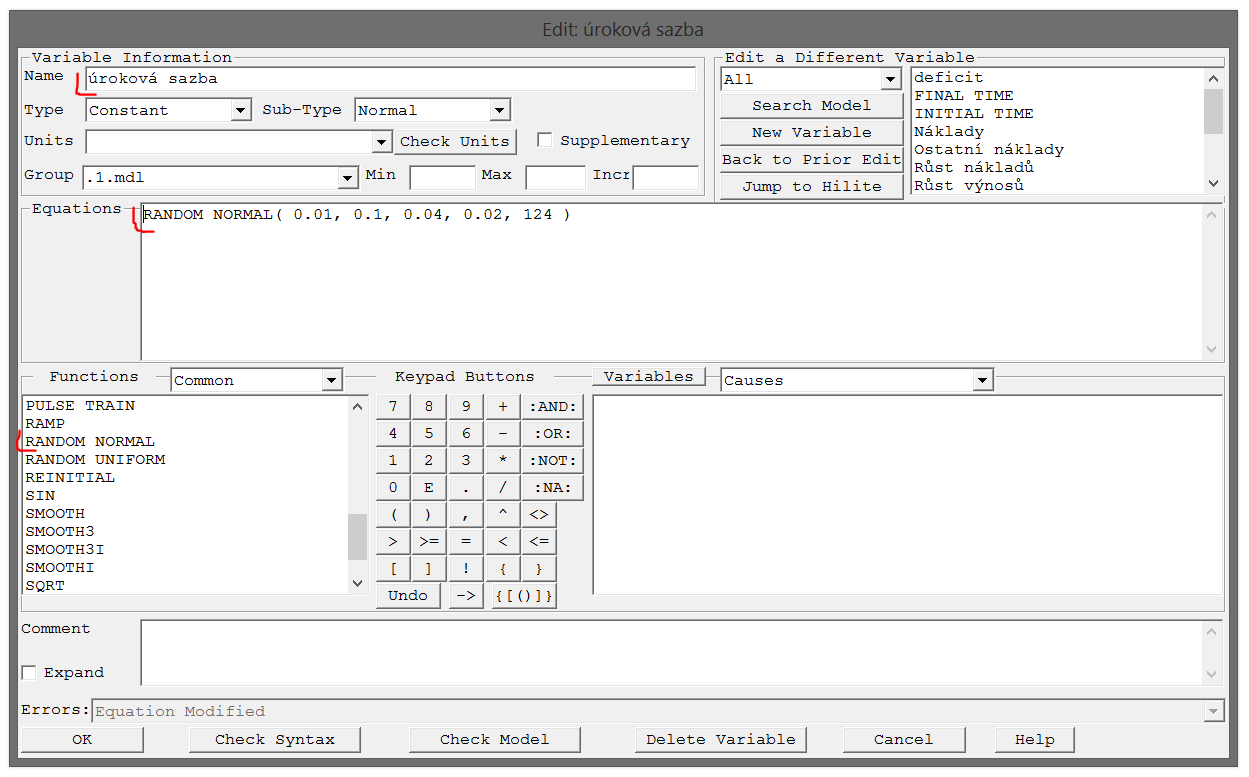
- úroková sazba = RANDOM NORMAL( 0.01, 0.1, 0.04, 0.02, 124 )
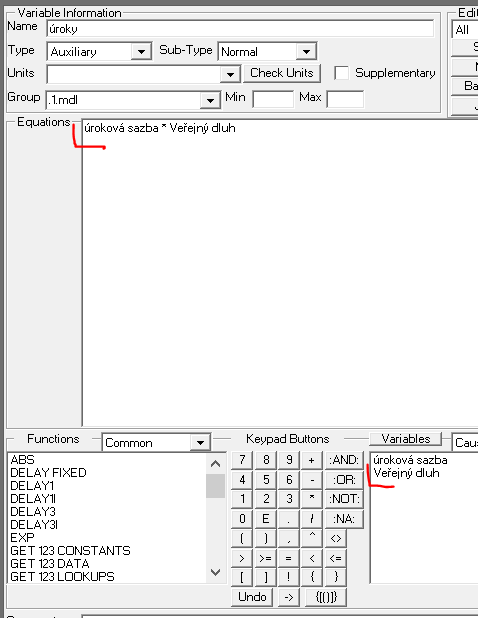
- úroky = úroková sazba * Veřejný dluh
- Zaplacené úroky = INTEG (úroky, 0)
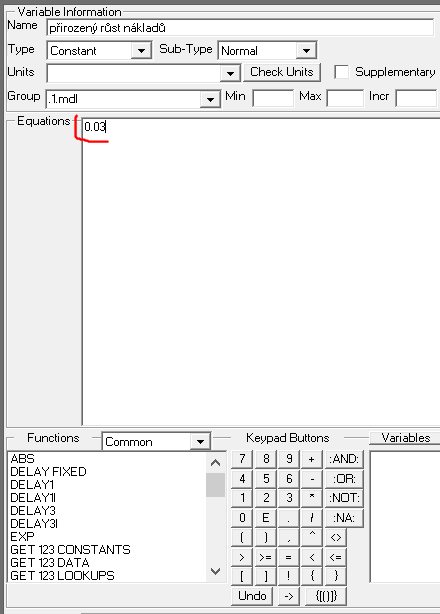
- přirozený růst nákladů = 0.03
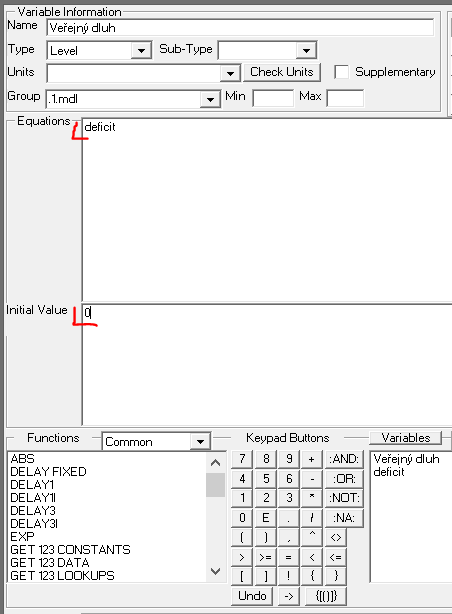
- Veřejný dluh = INTEG (deficit, 0)
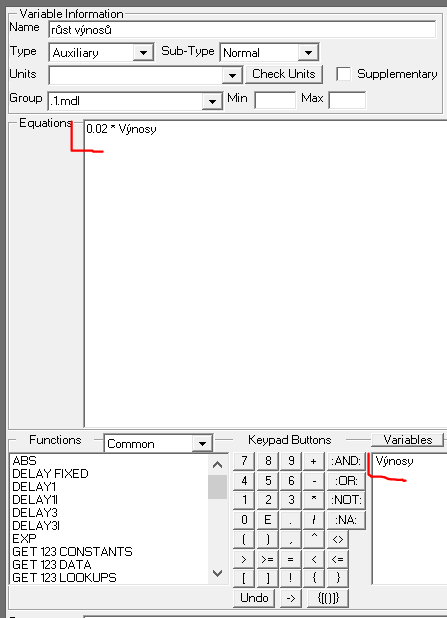
- růst výnosů = 0.02 * Výnosy
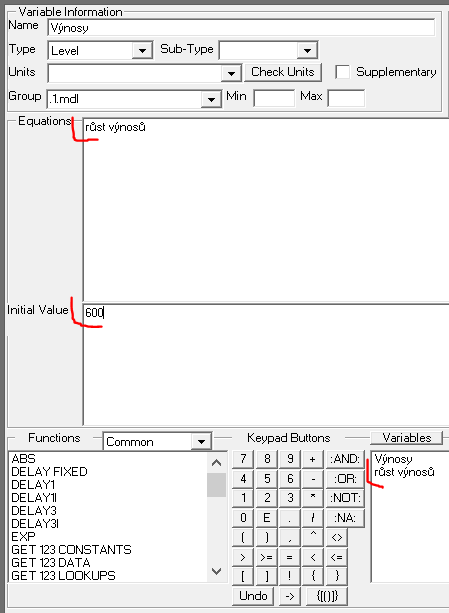
- Výnosy = INTEG (růst výnosů, 600)
| Nutná trpělivost S největší pravděpodobností budete své modely také vytvářet v prostředí Vensim. Proto se obrňte trpělivostí a modely průběžně ukládejte. Prostředí je staré a často narazíte na různé bugy (popisy políček programu se nepochopitelně přepisují, okna se přepínají, nejde potvrdit akci a ani z ní odejít jinak než přes Ctrl+Alt+Del a model tak ztratit), proto UKLÁDEJTE. |
Tyto informace se musí zanést do modelu. Tyto data se vloží do jednotlivých objektů (stavů, toků a proměnných) skrz tlačítko , jenž model přepne do stavů vkládání rovnic (začerní všechny názvy).
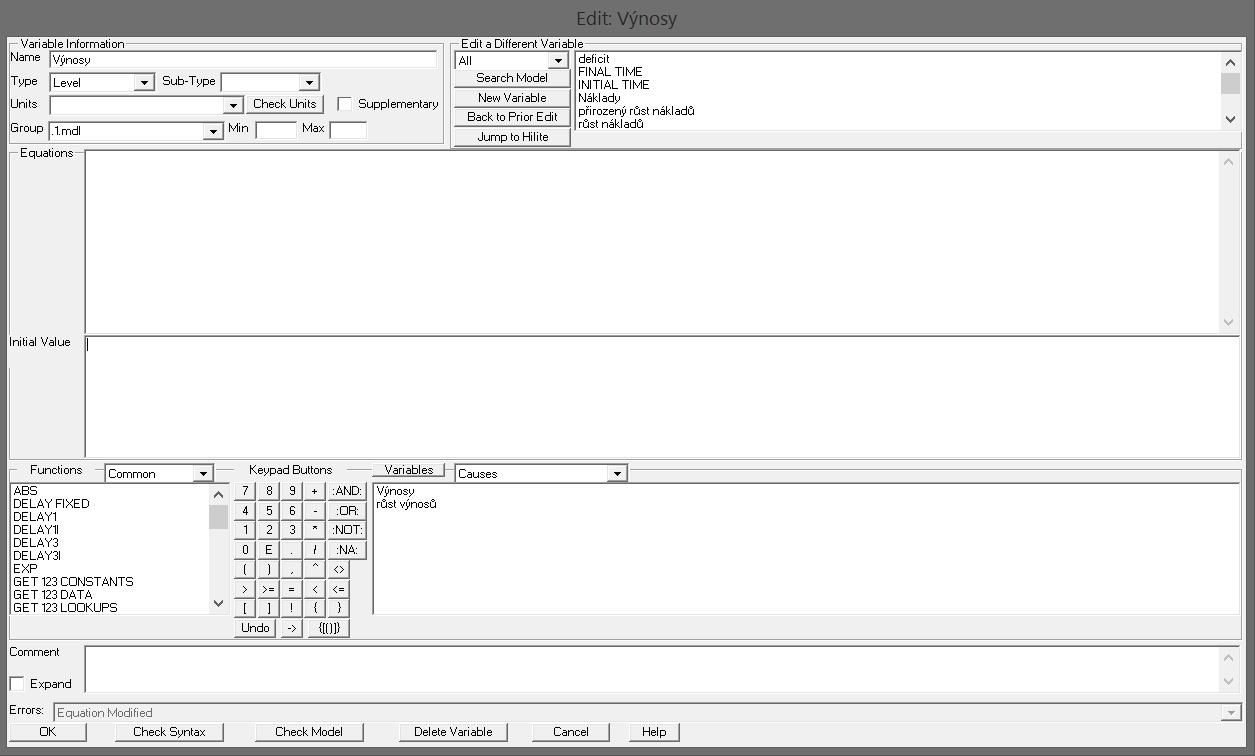
Začerněné názvy znamenají, že těmto objektům ještě nebyly přiřazeny žádné rovnice. Rovnice jednoduše zadáme přes kliknutí na název objektu.
Po kliknutí na stav se nám zobrazí výše zveřejněný obrázek. Pokud klikneme na tok nebo proměnnou, nezobrazí se velké pole „Initial value“, které má právě pouze objekt stav.
Celé okno se dělí na sekce „Variable Information“, „Edit a Different Variable“, „Equations“, „Initial Value“, „Functions“, „Keypad Buttons“, „Variables“.
Ve „Variable Information“ se jen ujistíme, že jsme opravdu klikli na Výnosy. Do „Equations“ se vloží rovnice a proměnné se do takové rovnice vkládají ze sekce „Variables“. Na screenu se nám nabízí Výnosy a růst výnosů. V této oblasti se zobrazují jen názvy objektů napojených na daný objekt (na Výnosy se váže růst výnosů, vazba daná spojem). Do rovnice nemůžeme zadat objekt, na který vybraný objekt nemá vazbu.
Funkce pro rovnice se vybírají z oblasti „Functions“, matematické znaky (+ - * /) přes „Keypad Buttons“ nebo prostě přes klávesnici. Desetinná čísla nepoužívají čárky, ale tečky (tj. 0,2 je 0.2). Do „Initial value“ (pouze pro stav) se zadá počáteční hodnota.
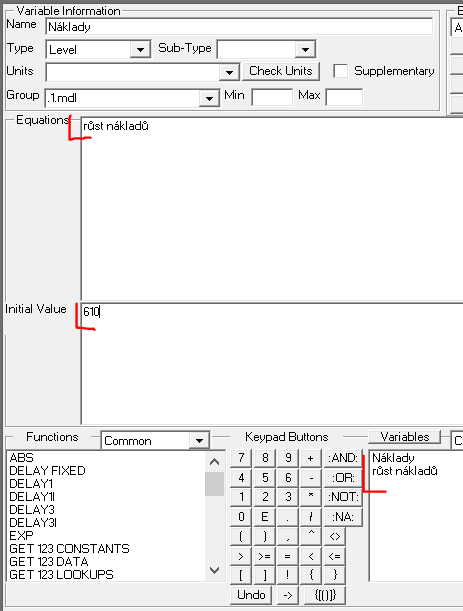
Stavy zadáme:
Náklady = INTEG (růst nákladů, 610)
| V rovnicích slovo „INTEG“ jasně říká, že objekt je stav. Pokud je rovnice INTEG(nové objednávky - vyřízené objednávky, 200), znamená to, že jde o stav s rovnicí nové objednávky - vyřízené objednávky a počáteční hodnotou 200. |
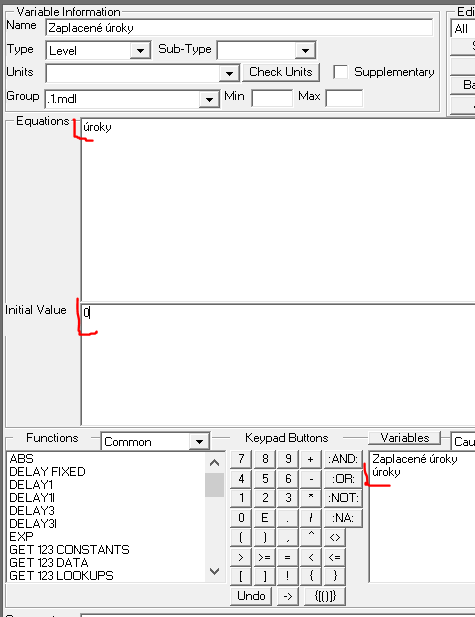
Zaplacené úroky = INTEG (úroky, 0)
Veřejný dluh = INTEG (deficit, 0)
Výnosy = INTEG (růst výnosů, 600)
Toky zadáme:
Deficit = Náklady + Úroky – Výnosy
růst nákladů = přirozený růst nákladů * Náklady
úroky = úroková sazba * Veřejný dluh
růst výnosů = 0.02 * Výnosy
Proměnné zadáme:
úroková sazba = RANDOM NORMAL( 0.01, 0.1, 0.04, 0.02, 124 )
přirozený růst nákladů = 0.03
Pokud jste prošli veškerým tím podrobným zadáváním rovnic, můžu ještě nakonec dodat, že rovnici jde rovnou i zkopírovat a rovnou vložit do Equations objekt po objektu :-) .
Spuštění modelu
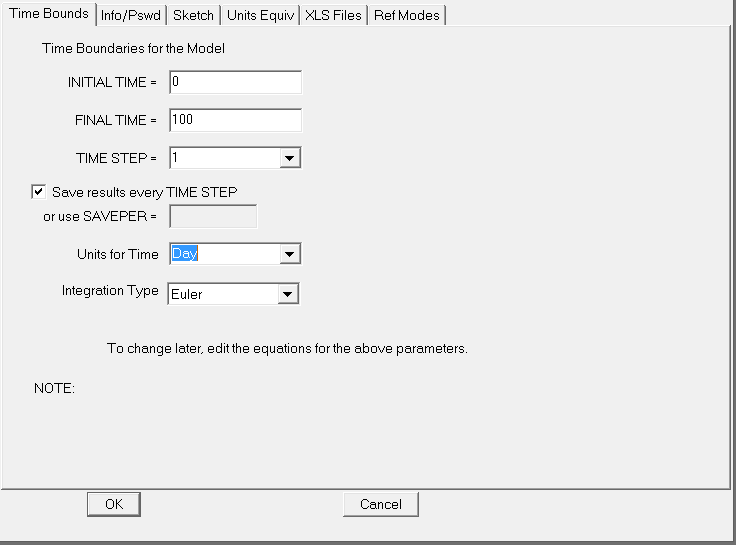
Klíčová funkce SFD je, že model lze spustit a vidět vývoje jednotlivých objektů. Přes Model / Settings (nebo úplně při zakládání modelu) se mohou nastavit hodnoty pro spuštění modelu.
To nejdůležitější:
- Initial time = počáteční čas
- Final time = čas, kdy se model zastaví
- Units for Time: co vlastně znamená „1“, jestli jeden den, jednu sekundu nebo jeden rok.
Pokud nastavení uložíme a spustíme tento model (vyplnili jsme rovnice všech objektů, tj. žádný objekt není v módu zadávání rovnic začerněný), model spustíme přes tlačítko .
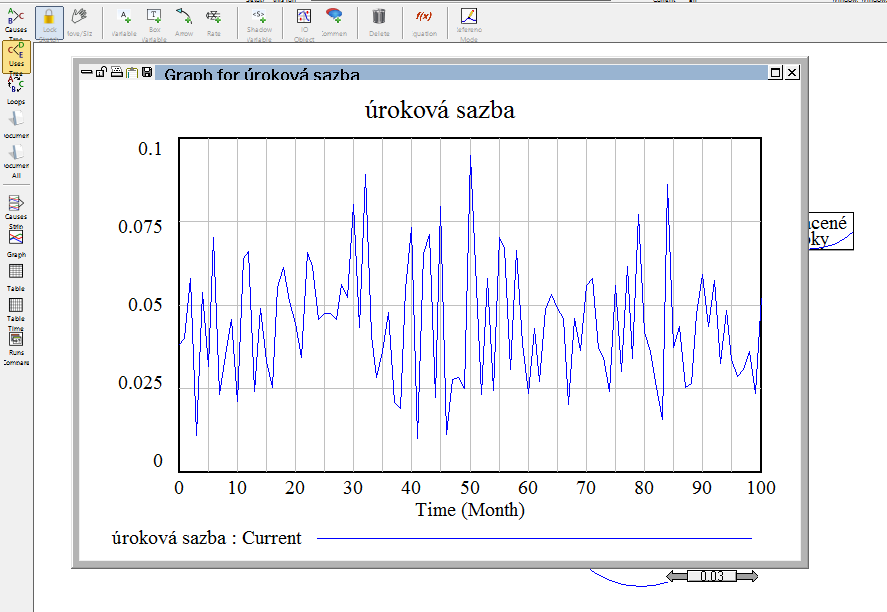
Na jednotlivých objektech najednou vidíme jejich vývoj (exponenciální), úroková sazba (která se generuje jako náhodné číslo, se pohybuje mezi omezujicími hodnotami a přirozený růst nákladů (jeho rovnice je jen 0.03) umožňuje s číslem pohybovat skrz šipky a vidět, jak se model mění.
Přes tlačítko můžeme jednotlivé grafy zvětšit, takže graf úrokové sazby je:
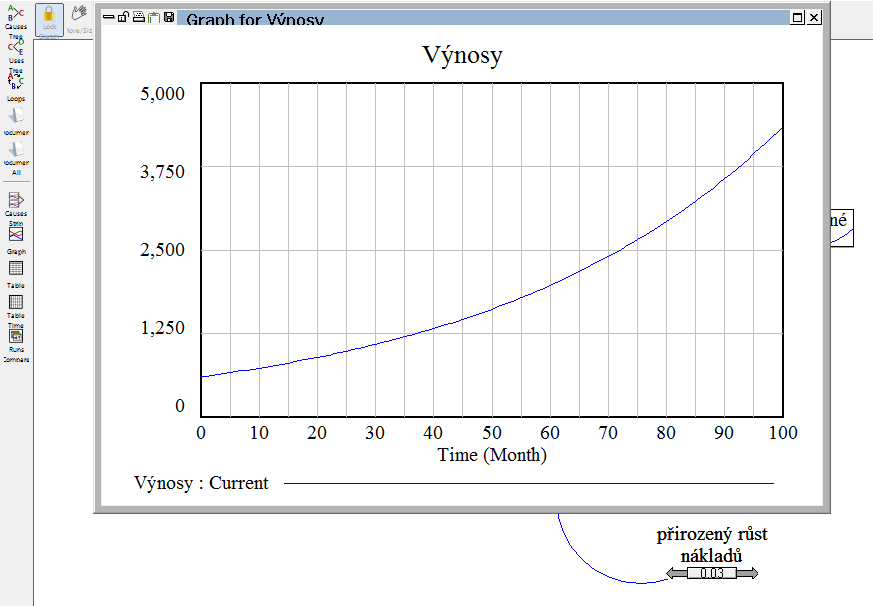
Nebo Výnosů:
Další příklady modelů
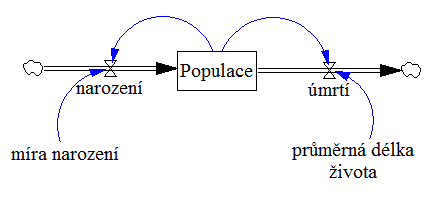
Životní cyklus
Zdroj [3]
Rovnice:
- narození = míra narození * Populace
- Populace = narození – úmrtí
- Průměrná délka života = 8
- Míra narození = 0.03
- Úmrtí = Populace / průměrná délka života
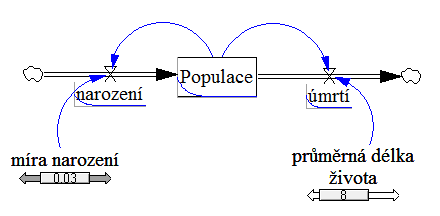
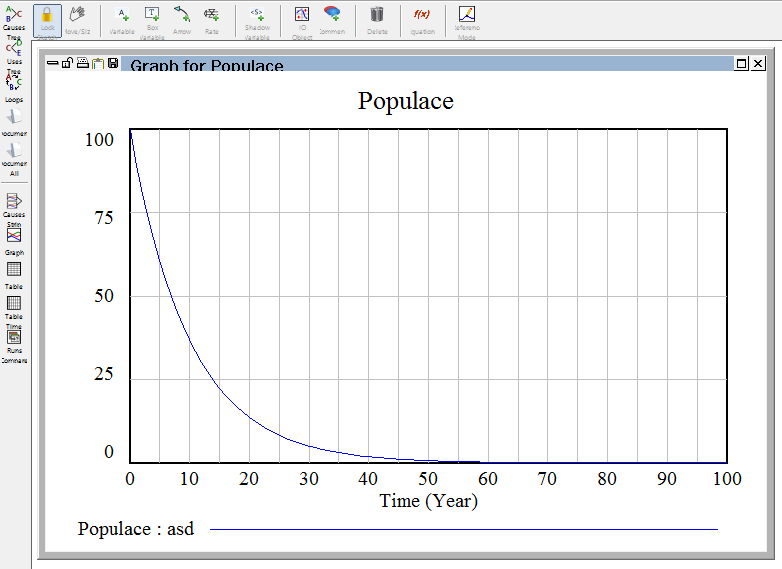
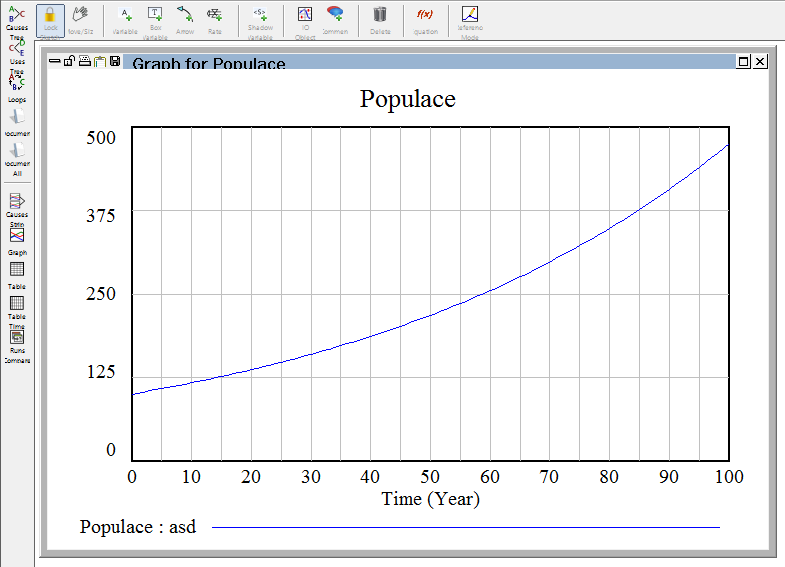
Výsledek (spuštění modelu):
Je vidět, že populace kompletně vymře do cca 60 let s mírou narození 0.03 a průměrnou délkou života 8 let.
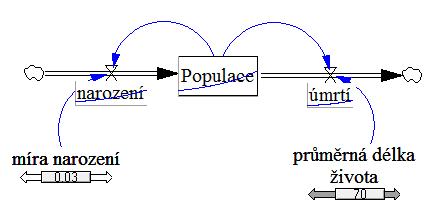
Zvýšíme tedy průměrnou délku života na 70 let:
Populace už nevymírá a postupně se počet obyvatel zvyšuje.
Zdroje
Literatura & online
[1] MILDEOVÁ, Stanislava a Viktor VOJTKO. Selected chapters of system dynamics. 1st ed. Bratislava: Kartprint, 2006, 137 s. ISBN 80-888-7060-7.
[2] MILDEOVÁ, Stanislava a Viktor VOJTKO. Systémová dynamika. Vyd. 2., přeprac. V Praze: Oeconomica, 2008, 150 s. ISBN 978-80-245-1448-2.
[3] MILDEOVÁ, Stanislava a Viktor VOJTKO. Systémová dynamika: tvorba modelu. Vyd. 1. Praha: Oeconomica, 2011, 150 s. ISBN 978-80-245-1842-8.
[4] RICHARDSON, George P. Problems with causal-loop diagrams. In: [online]. [cit. 2014-06-14]. Dostupné z: http://www.systems-thinking.org/intst/d-3312.pdf
[5] Stock and Flow Diagrams. Business Prototyping Blog [online]. [cit. 2014-06-14]. Dostupné z: http://www.business-prototyping.com/step-by-step-tutorials/introduction-to-system-dynamics/stock-and-flow-diagrams/
[6] Stock and Flow diagram. In: Simulace.info [online]. 2014. vyd. [cit. 2014-06-14]. Dostupné z: http://www.simulace.info/index.php/Stock_and_flow_diagram
Videa