Statistics101: Probability distributions/cs

Úvod

Co je to pravděpodobnost

Uvažujeme pokus spočívající v hodu symetrickou (homogenní) mincí. Tento experiment má dva možné výsledky:

•   Na minci padl rub

•   na minci padl líc

Běžně činíme v této souvislosti následující prohlášení:

(1) pravděpodobnost toho, že na minci padne rub, je rovna ½.

Odhlédneme-li od toho, že vlastně ještě nevíme, co pravděpodobnost je, není obtížné zjistit dva zdroje důvěry v rozumnost tohoto výsledku:

(2) Logická spekulace . Není důvod, proč by na symetrické minci měl častěji padat rub nebo líc

(3) Zkušenost . Opakujeme-li pokus mnohokrát a zjišťujeme-li četnosti Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_n} výsledku rub po n pokusech, budou se relativní četnosti (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle S_n/n } ) postupně stabilizovat v okolí čísla ½.

Je samozřejmě otázkou spíše filozofického charakteru, do jaké míry a v jakém smyslu je spekulace (2) založena na zkušenosti (3). A jakým mechanismem jsou zkušenosti typu (3) ukládány do vědomí člověka, když ve velké většině podobné pokusy pro velká n nekoná.

Předmětem teorie pravděpodobnosti je tedy studium matematických modelů náhodných pokusů.

Uvážíme-li příklad pokusu se symetrickou mincí, můžeme vymezit tento pojem jako pokus, jehož výsledek není jednoznačně určen podmínkami, za kterých je vykonáván , přičemž tyto výsledky vykazují statistickou stabilitu typu (3), která vlastně umožňuje hovořit o pravděpodobnostech výsledků pokusu . Teorie pravděpodobnosti modeluje náhodný experiment způsobem, který umožňuje nejen deduktivní ověření této stability, ale i odhadování zákonitostí, které leží mimo dosah běžné zkušenosti.

S náhodným pokusem je vždy spojena neprázdná množina Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \Omega} všech výsledků pokusu.

Pravděpodobnostní rozdělení

Prvky Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \omega \in \Omega } se nazývají elementární jevy .

Pravděpodobnostní rozdělení je vlastně zobrazení, které každému elementárnímu jevu (prvkům z množiny Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \omega \in \Omega } ) přiřazuje jejich pravděpodobnost. (Číslo mezi 0 a 1). Podrobněji k definicím naleznete na pravděpodobnostní rozdělení

Ukázky

Pojdmě si vše vysvětlit na rozboru názorných příkladů.

Diskrétní rozdělení

V našem hypotetickém městě se začala šířit infekční nemoc Sars-cov-3000. Tato nemoc je léčitelná a nezpůsobuje dlouhodobé komplikace. V nemocnici je léčena přípravkem Prymlo. Jeho aplikace je komplikovaná a můžeme proto podat léčbu právě 10 lidem.

Ukazuje se, že léčba není vždy účinná. V průběhu času jsme naměřili, že je 60% pravděpodobnost, že se léčba povadla a 40% pravděpodobnost, že léčba selhala.

To znamená, že v průměru je každý den vyléčeno 6 lidí z těch 10. To ale neznamená, že bude každý den vyléčeno právě 6 lidí. Některé kdy může být vyléčeno méně a některé dny více.

A právě kolik lidí bude vyléčeno každý jednotlivý den nám určuje pravděpodobnostní rozdělení. Představme si, že chceme nějak předvídat hodnotu X (počet lidí, kteří budou vyléčeni zítra).

To znamená, že chceme například zjistit, jaká je pravděpodobnost, že zítra bude vyléčeno právě šest lidí Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(X = 6)} nebo jaká je pravděpodobnost, že zítra bude vyléčeno něco mezi čtyřmi a osmi lidmi P(4 ≤ X ≤ 8)?

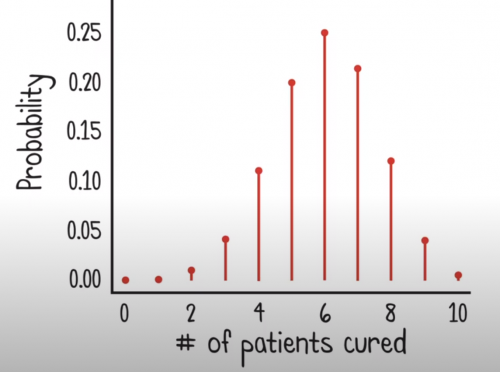
K tomu, abychom tyto hodnoty dokázali určit, potřebujeme znát pravděpodobnostní rozdělení. V rámci našeho hypotetického města jsme predikovali, že rozdělení pravděpodobnosti vypadá

Toto je binomické rozdělení, které popisuje četnost výskytu náhodného jevu v n nezávislých pokusech, v nichž má jev stále stejnou pravděpodobnost. (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X ~ Bi(n, p)} )

Z pravděpodobnostního rozdělení můžeme hned vidět, že hodnota pro 6 je 0.25. (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(X = 6) = 0.25} ). Takže je 25%, že v patřičný den bude vyléčeno právě 6 pacientů.

---

Příklad:

Jaká je tedy pravděpodobnost, že že zítra bude vyléčeno něco mezi čtyřmi a osmi lidmi (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(4 \leq X \leq 8)} )?

Řešení:

P(4 ≤ X ≤ 8) = P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7) + P(X = 8) = 0.9

Pravděpodobnost, že bude vyléčeno mezi čtyřmi a osmi lidmi, je 90%.

---

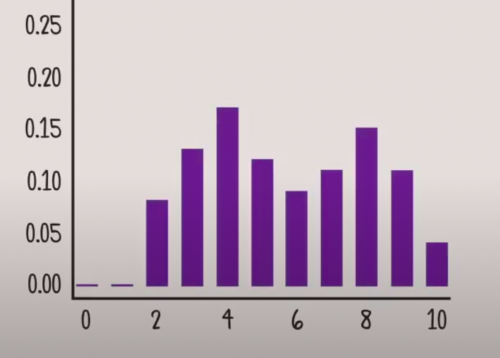
Po delší době se ukazuje, že naše distribuční funkce neplatí. S větším množstvím dat zjištůjeme, že počty vyléčených pacientů vypadají

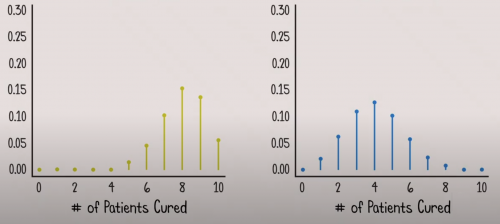
Ukázalo se totiž, že lék Prymlo distribuují dva dodavatelé. Jeden s účinnou látkou Pifcer a druhý s účinnou látkou Spadnik. Každý den byl náhodně vybrán lék od jednoho dodavatele, vždy s 50% pravděpodobností. První přípravek měl však účinnost 80% a druhý pouze 40%. A proto bylo výsledné rozdělení mixem 2 rozdělení

Po tomto zjištění bylo možné distribuovat léčivo Pifcer ve větší míře a zvýšit tak počet vyléčených.

Poslední část, na kterou se můžeme podívat, je pravděpodobnost nákazy. Z vedených statistik ve městě vyšlo, že pravděpodobnost, že se zítra nakazíte, je 0.001.

Město má v současnosti 20 000 dříve nenakažených obyvatel. Jak vypadá pravděpodobnostní rozdělení?

Za předpokladů, že jsou naše data správná, pak se jedná opět o binomiální rozdělení Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Bi(20000, 0.001)} . Problémem je, že při výpočtu binomického rozdělení Binomické rozdělení se pracuje s faktoriály a při výpočtech s takovými čísly bychom záhy narazili na problémy. Výhodou je, že pro binomická rozdělení, kde je p malé, můžeme velice dobře aproximovat pomocí Pissonova rozdělení. Poissonovo rozdělení

Z toho celkově máme, že rozdělení nově infikovaných pacientů je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Pois(20)} a při použití léčiva Pifcer (80% účinnost) je počet vyléčených Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Pois(20*0.8) = Pois(16) } a počet neúspěšně vyléčených je Pois(4).

Zde jsme si na hypotetickém příkladu ukázali motivaci a základní použití diskrétního pravděpodobnostního rozdělení. Více příkladů k procvičení najdene v Typy diskrétních rozdělení.

Spojité rozdělení

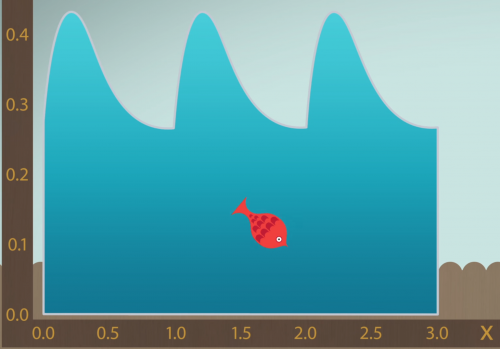
Představme si akvárium. Pro jednoduchost si představme pouze jednu stranu akvaria. Takové 2D akvarium. Naším cílem je lokalizovat v akváriu rybu. Chceme určit, jaká je horizontální souřadnice ryby v akváriu. Je zřejmé, že hodnota souřadnice může nabývat hodnot ze spojitého intervalu (šíře akvária).

Když si představíme, že akvárium má plochu 1. Pak pravděpodobnost, že se ryba nachází v nějaké ploše, je rovna velikosti této plochy.

Jaká je pravděpodobnost, že se ryba nachází na souřadnici 1.5? Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(X = 1.5)}

Tady se ukazuje hlavní neintuitivnita spojitých rozdělení. Pravděpodobnost, že se ryba nachází na souřadnici 1.5 je
0
! Souřadnice totiž mohou nabývat nekonečně mnoha hodnot. Pravděpodobnost, že se ryba nachází
přesně
na nekonečně malé ploše je limitně nulová. Když se vrátíme k představě přes plochu, tak se jedná o plochu úsečky a ta je nulová.

Jde o to, že samotná hodnota je na rozdíl od diskrétních hodnot vždy pouze nějaká aproximace. Souřadnice 1.5 je totiž souřadnice 1.500000000... A proto nemá smysl mluvit o samotné hodnotě a vždy se bavíme o nějakém intervalu.

Proto když ryba proplave mezi body 1 a 2. Překoná nekonečné množství souřadnic. To je známí problém, který řešili již staří řekové. Proto má cenu bavit se pouze o plochách a ne o jednotlivých bodech. (Měření pravděpodobnosti bytí v nekonečně malém prostoru v kokrétním časovém kroku je totiž ergo vždy nulová.)

Zavadíme proto koncept hustoty pravděpodobnosti.

“Hustota pravděpodobnosti (hustota rozdělení pravděpodobnosti, anglicky Probability Density Function, PDF) v teorii pravděpodobnosti je funkce jejíž integrací na kterémkoli vzorku (podmnožině prostoru elementárních jevů) vyjde relativní pravděpodobnost, že hodnota náhodné proměnné by se rovnala tomuto vzorku. PDF se používá ke stanovení pravděpodobnosti , že náhodná proměnná spadá do určitého intervalu hodnot namísto libovolné jediné hodnoty. Tato pravděpodobnost je určena integrálem PDF této proměnné nad uvedeným rozsahem, který si lze představit jako plochu ohraničenou funkcí hustoty a vodorovnou osou, a mezi nejnižší a nejvyšší hodnotou daného intervalu. Funkce hustoty pravděpodobnosti je všude nezáporná a její integrál v celém prostoru je roven 1.”

Ona integrovaná funkce je přesně hranice našeho ukázkového nesymetrického 2D akvária.

---

Příklad:

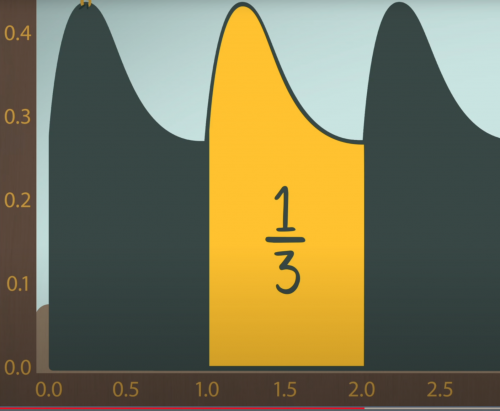
Když chápeme základní pojmy, můžeme si tedy položit otázku. Jaká je pravděpodobnost, že se ryba v akváriu nachází mezi souřadnicemi 1 a 2? P(1 ≤ X ≤ 2)

Řešení:

Pro samotnou integraci bychom potřebovali znát tvar funkce hustoty pravděpodobnosti. Pokud si ale vzpomeneme, že nám integrál počítá onu plochu pod křivkou, můžeme si všimnout, že se plocha mezi body 1 a 2 stejná, jako mezi body 0;1 a 2;3. Plocha pod křivkou je tedy 1/3 celkové plochy, kterou jsme určili jako 1;

Pravděpodobnost, že se bude ryba nacházet mezi souřadnicemi 1 a 2, je 33.33%.

---

Příklad:

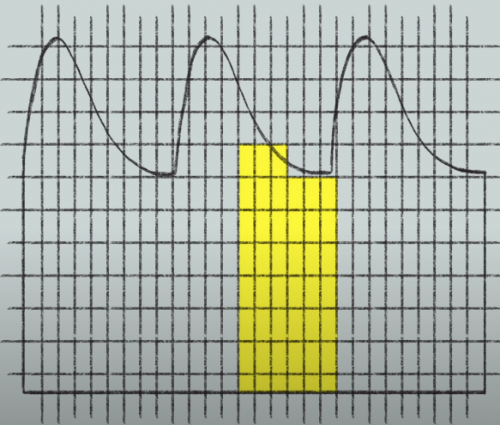
Co kdybychom chtěli zjistit pravděpodobnost, že se ryba v akváriu nachází mezi souřadnicemi 1,5 a 2? P(1,5 ≤ X ≤ 2)

Řešení:

Zde už nám nepomůže trik se symetrií. Jelikož neznáme tvar hustoty pravděpodobnosti (pak bychom úlohu řešili integrací, abychom spočítali plochu pok křivkou), uchýlíme se k aproximaci. Můžeme totiž spočítat plochu alespoň přibližně

Pravděpodobnost, že se bude ryba nacházet mezi souřadnicemi 1,5 a 2, je přibližně 14%.

---

Zde jsme si na hypotetickém příkladu ukázali motivaci a základní použití spojitého pravděpodobnostního rozdělení. Více příkladů k procvičení najdene v Základní typy rozdělení pravděpodobnosti spojité náhodné veličiny.