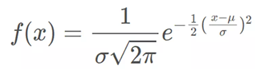Interpretation of MC simulation results (Stochastic methods)/cs

Zpracování a interpretace výsledků je velmi důležitá část simulace a neměla by být podceňována. V případě, že se v modelu vyskytují náhodné veličiny, tak to znamená, že i výsledky jsou náhodné veličiny. Výsledkem modelu je buď bodový nebo intervalový odhad. Intervalový odhad by měl být použitý spíše než bodový.

Validace a verifikace

Pro získání správných výsledků je důležité provést validaci a verifikaci výsledků. Provedení validace a verifikace výsledků jsou zásadní kroky, díky kterým se dozvíme, že je náš simulační model Monte Carlo věrohodný a užitečný. Validace ověřuje, že náš model reprezentuje reálný systém nebo problém, který se snažíme nasimulovat. A verifikace kontroluje, že je náš model implementován správně a neobsahuje žádné chyby nebo omyly. Validace a verifikace je důležitá. Pokud nedojde k provedení těchto dvou kroků je možné, že budou modely ukazovat zavádějící nebo nepřesné výsledky, které nějakým způsobem mohou ovlivnit rozhodnutí a výsledky projektu.

Jak validovat model?

Validace je subjektivní a opakující se proces. Validace zahrnuje porovnání předpokladů, vstupů, výstupů a chování našeho modelu s dostupnými daty a znalostmi, které jsou dostupné z reálného systému nebo problému. Pro validaci modelu můžeme použít různé techniky. Mezi takové techniky řadíme například analýza citlivosti, odborný posudek nebo historická data.

Analýza citlivosti zahrnuje změnu jedné nebo více vstupních proměnných a sleduje to, jak ovlivní výstupní proměnné. Díky tomu jsme schopni a může nám pomoct identifikovat nejvlivnější a nejisté faktory v našem modelu. Odborný posudek je konzultace s odborníky, kteří rozumí té dané problematice, zúčastněnými stranami nebo kolegy, kteří již mají zkušenosti nebo znalosti o reálném systému nebo problému. Historická data porovnávají výstupy, které nám dal náš model, se skutečnými nebo pozorovanými daty z minulosti. Na základě, kterých jsme schopni posoudit jak přesný a realistický jsou naše modelové předpovědi a předpoklady.

Jak verifikovat model?

Verifikace je objektivní a systematický proces. Verifikace zahrnuje testování a ladění implementace modelu a kódu. Pro verifikaci modelů můžeme použít logické a syntaktické kontroly. Tyto kontroly odhalí a opraví případné syntaktické chyby, překlepy nebo chybějící prvky v kódu. Testovat můžeme každý komponent nebo funkci modelu samostatně a nezávisle. Také můžeme testovat interakce a vazby mezi komponenty a funkcemi našeho modelu. Díky tomu ověříme model a zjistíme, zda funguje tak, jak má a jestli zobrazuje očekávané výsledky.

Nástroje pro validaci a verifikaci

Modely Monte Carlo lze validovat a verifikovat pomocí různých nástrojů a softwarů. Jedním takovým nástrojem je Excel. V Excelu lze provádět základní simulace Monte Carlo pomocí vestavěných funkcí a vlastností. Excel můžeme využít k vytváření a testování logiky modelu, vstupů a chování nebo také i k provádění analýzy citlivosti a porovnání výstupů modelu s historickými daty. Jako další nástroj pro validaci a verifikaci můžeme použít @RISK nebo Crystal Ball. Jedná se o specializované programy, které na rozdíl od Excelu, umožňují pokročilé funkce a vlastnosti pro simulaci Monte Carlo. Můžeme je využít pro vytváření a testování logiky modelu, vstupů, výstupů a chování, nebo k provádění analýzy citlivosti, expertního posouzení a porovnávání výstupů modelu s historickými daty. Oba dva zmíněné nástroje v sobě mají verifikační nástroje a na základě toho dokážou kontrolovat kód modelu a říct, jestli obsahuje chyby nebo ne.

Normální distribuce

Výsledky generované simulací monte Carlo budou často tvořit normální distribuci, takže Gaussovu křivku.

Vzorec

X = hodnota proměnné nebo zkoumaných dat

F(x) = pravděpodobnostní funkce

μ = průměr

σ = směrodatná odchylka

Normální distribuce je rozdělení pravděpodobnosti, které je symetrické podle průměru. Ukazuje, že data, která jsou okolo průměru se objevují častěji než data, která jsou daleko od průměru.

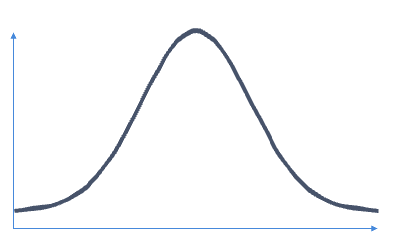
V grafické podobě je normální distribuce zobrazena jako „zvonová křivka“ neboli také Gaussova křivka.

Nejvyšší bod na křivce ukazuje nejpravděpodobnější událost v řadě dat (průměr). Ostatní možné hodnoty jsou symetricky rozmístěné okolo průměru. Díky tomu je vytvořena klesající křivka na obě strany z vrcholu, distribuce symetricky klesá kolem průměru. Šířka grafu je definována směrodatnou odchylkou.

Jedná se o typ symetrického rozdělení. Symetrické rozdělení poznáme tak, že když graf rozdělíme napůl, vytvoří dva stejné zrcadlové obrazy.

Vlastnosti normální rozdělení

Normální rozdělení má několik důležitých vlastností a tyto vlastnosti ho definují. Jedná se o:

- Průměr – průměr všech dat v souboru (=PRŮMĚR(G:G) v Excelu)

- Medián (=MEDIÁN(G:G) v Excelu)

- Modus

- Směrodatná odchylka – kvantifikace variability rozptylu dat v souboru daných hodnost kolem průměru (=STDEV(G:G) v Excelu)

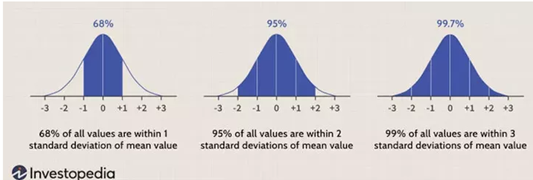
Empirické pravidlo

Toto pravidlo popisuje, kde se objeví většina dat v normálním rozdělení. Pro jednu směrodatnou odchylku od průměru je u normálního rozdělení 68,2 % hodnot. 95,4 % pozorování bude spadat do dvou směrodatných odchylek. A v rozmezí tří směrodatných odchylek bude 99,7 % hodnot.

Příklad

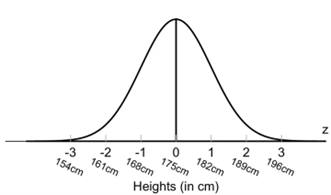
Například bychom chtěli zjistit jaké je rozložení lidské výšky. Z grafu níže vidíme, že průměrná výška populace je 175 cm. Do dat jsou započítáni muži i ženy. To znamená, že většina lidí odpovídá průměru, takže měří 175 cm. Dále z grafu dokážeme vyčíst, že existují nižší i vyšší lidé. Z výsledků vidíme, že 99,7 % lidí měří mezi 154 cm a 196 cm. Pouze 0,3 % lidí z celé populace jsou vyšší než 196 cm a nižší než 154 cm. Jedná se o poměrně vzácné lidi.

Výsledky

Výsledky simulace Monte Carlo jsou v tabulce a je potřeba je dále analyzovat. Pomocí Excelu je můžeme zpracovat/zanalyzovat. Jednou z možností je, že si vytvoříme histogram výsledků, který je častým výsledkem simulace. Histogram zobrazuje všechny možné výsledky a pravděpodobnost, že ke každému výsledku dojde. Dále můžeme pouze vytvořit průměr, jak uvidíme v ukázce později.

Histogram

Histogram je nezbytnou součástí, protože zobrazuje vizuální reprezentaci dat.

Také umožňuje snadno zjistit, které hodnoty se nejčastěji vyskytují a které nejméně. Na vodorovné ose jsou znázorněny měřená data a svislé ose počet pozorování v každé přihrádce (bin).

Osu x máme od minimální hodnoty po maximální hodnotu pro jednu číselnou proměnnou souboru dat. Intervaly jsou stejně veliké a nazýváme je přihrádky (bin). Histogram nám ukazuje, jak často hodnota spadá do konkrétního binu. Výška každého sloupce nám udává počet hodnot v sadě dat, které spadají do konkrétního binu.

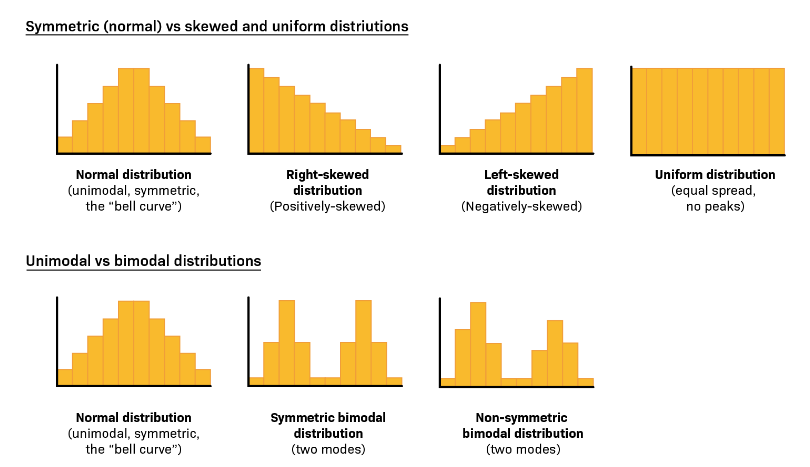
Máme různé druhy histogramu:

- Symetrický

- Zkosený doprava

- Zkosený doleva

- Unimodální

- Multimodální

Symetrický graf poznáme tak, že od středu na obě strany vypadá přibližně stejně. U symetrického je průměr, medián a modus přibližně stejný. Pokud je graf zkosený doprava, má na obrázku delší pravý konec. Pravozkosený graf jinak můžeme označit jako kladně zkosený. Naopak graf zkosený doleva má protažený levý konec grafu a nazýváme ho jako záporně zkosený. Doprava zkosené bývají většinou proměnné, které musí být kladné a to je například vzdálenost, velikost nebo čas. Doleva zkosený bude věk úmrtí z přirozených příčin, protože častěji přirozeně umírají starší lidé než mladší.

Histogramy můžeme mezi sebou porovnat. Avšak histogramy musí mít stejný minimální a maximální hodnoty na ose x a ose y a velikost binů. V případě, že mají rozdílné měřítka, mohou být výsledky zavádějící. Dále bychom meli mít grafy vertikálně, pod sebou, abychom lépe viděli rozdíly ve výsledcích.

Histogram je graf, který vytvoříme v Excelu pomocí grafu nazývaný histogram. Vybereme si vhodná data, které chceme zobrazit v grafu-> vložení -> vložit statistický graf – histogram.

Prezentace výsledků

Při prezentaci výsledků bychom měli uvádět a provádět tyto informace a činnosti:

- Úplný a důkladný popis modelu a jeho rovnic. Měli bychom uvést všechny použité vzorce a úplné odkazy. Definovat všechny pojmy. Popsat kvalitativně hlavní výhody a omezení použitých modelů. Cílem je, abychom poskytli kompletní popis, aby mohl kdokoliv hodnocení nezávisle zopakovat a ověřit. Důležitá je transparentnost a reprodukovatelnost.

- Podrobné informace o vybraných vstupních distribucích. Měli bychom důkladně zdokumentovat a předat kritické údaje a metody, které dávají podstatný kontext pro pochopení a interpretaci výsledků hodnocení. Dále bychom měli vytvořit grafy a tabulky pro vizuální zpracování písemných informací. Konkrétně graf hustoty pravděpodobnosti (PDF) a graf kumulativní distribuční funkce (CDF). Grafy ukazují rozdílné, ale důležité poznatky. Pomocí grafů jsme schopni porovnat experimentální data a přiřazené rozdělení.

- Podrobné informace a grafy pro každou distribuci výstupů. Pro každé vstupní rozdělení je potřeba udělat graf CDF a PDF.

- Diskutujte o přítomnosti nebo nepřítomnosti závislostí a korelací. Výstup analýzy může ovlivnit kovariance mezi vstupními proměnnými.

- Vypočítat a prezentovat bodové odhady. Bodové odhady vypočítáme pomocí zavedených protokolů. Měli bychom uvést použitý matematický model a hodnoty, které jsme použili pro jednotlivé vstupní parametry při výpočtu. Dále bychom měli napsat, kam spadá bodový odhad v rozdělení vygenerovaném analýzou Monte Carlo. Porovnat bodové výsledky a výsledky Monte Carlo, zda jsou srovnatelné. Pokud ne, je potřeba rozdíl zmínit.

Příklady

Příklad 1

Jste ministrem financí a čelíte následujícímu problému: vaše vláda prohraje mezinárodní arbitráž se zahraničním investorem. Ve hře je 40 miliard Kč.

-Daňové příjmy a vládní výdaje v jednotlivých měsících jsou z normálního rozdělení podle následujícího schématu: -Začáteční zůstatek na účtech vlády je 100 mld. KČ.

-Jste si téměř jisti, že v říjnu prohrajete a budete muset zaplatit, ale současný rozpočet s tím nepočítal, takže budete muset vydat pokladniční poukázky předem, abyste zlepšili cashflow, pokud bude hotovost chybět.

-Jaká je pravděpodobnost, že nebude dostatek prostředků na vyplacení odškodnění a budete muset vydat pokladniční poukázky?

Interpretace výsledku

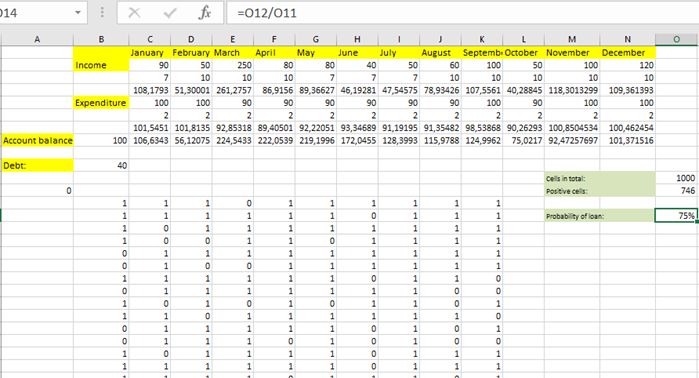
Na tomto obrázku vidíme výsledek. Máme tři hodnoty, které jsou důležité. První je cells in total, dále je to positive cells a třetí důležitá hodnota je probability of loan. Cells in total nám udává počet pokusů, které jsme udělali (tabulka 0 a 1, kterou vidíme). Positive cells nám říká, kolik hodnot z tabulky je kladných, tudíž kolikrát je v tabulce zobrazeno číslo 1. Výsledek, který jsme zjistili nám říká probability of loan. Jaká je pravděpodobnost půjčky. V tomto příkladě nám vyšlo, že je 75 % pravděpodobnost toho, že si budou muset vzít půjčku. Tuto hodnotu jsme získali tak, že jsme vydělili počet kladných hodnot počtem celkových pokusů.

Příklad 2

Jste manažerem farmaceutické společnosti a musíte se rozhodnout, kolik vakcín proti chřipce letos vyrobíte.

-Poptávka po vakcínách je z rovnoměrného rozdělení <400 000;800 000>. Jednou za deset let však v průměru vypukne chřipková epidemie, která vyvolá mezi lidmi paniku a poptávka po vakcínách stoupne. Pak se pohybuje od rovnoměrného rozdělení <700 000;1 500 000>.

-Regulovaná koncová cena vakcíny je 179 Kč. 9 % ceny tvoří DPH a dalších 29 % ceny bez DPH je distribuční marže.

-Variabilní náklady na jednu dávku vakcíny jsou cca 30 Kč a fixní náklady na výrobu jsou 40 mil. KČ.

-Společnost může vyrábět pouze plné dávky na 100 000 ks.

-Kolik vakcín by měla vyrobit, aby maximalizovala zisk?

Interpretace výsledku

Zde vidíme výsledek příkladu. V prvním řádku máme očekávaný zisk, druhý řádek ukazuje, jaká může být maximální ztráta a ve třetím řádku máme počet vakcín uvedený ve stovkách. Dále jsou v řádcích možné zisky, ze kterých je udělán průměr (řádků je více, než vidíme na obrázku). Z tohoto výsledku můžeme vidět, že by firma měla vyrobit 700 000 kusů vakcín. K číslu 700 000 jsme došli tak, že jsme u expected profit udělali průměr celého sloupečku, kde máme možné profity. A tam, kde nám vyšlo nejvyšší číslo očekávaného profitu (v tomto případě 17 935 562), tak tolik by měla firma vyrobit vakcín.

Příklad 3

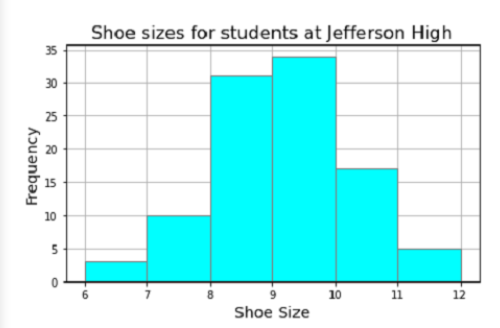
Na histogramu vidíme výsledek rozdělení 100 velikostí bot studentů ze střední školy. Kolik studentů má menší velikost než 8?

Interpretace výsledku

Z grafu lze vyčíst, že máme 3 studenty s velikostí bot mezi 6-7, 10 studentů s velikostí bot mezi 7-8, 31 studentů s velikostí bot mezi 8-9, 34 studentů s velikostí mezi 9-10, 17 studentů s velikostí mezi 10-11 a 5 studentů s velikostí 11-12.

Na základě tvaru grafu můžeme říct, že se jedná o symetrické rozdělení. Střed je kolem velikosti 9. A celkem 13 studentů má menší velikost než 8.

Příklad k procvičení

Zadání

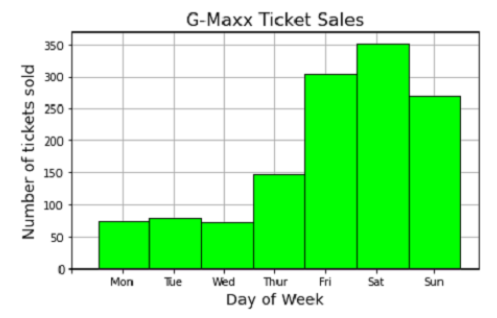
Výzkumný analytik zaznamenává množství vstupenek, které kino G-MaXX prodá za týden. Divadlo má 3 různé obrazovky a chce upgradovat na čtvrtou. Níže uvedený histogram znázorňuje rozložení prodeje vstupenek za fiskální týden v roce 2020. Popište tvar histogramu a určete, který den má obvykle největší prodej vstupenek.

Řešení

Histogram ukazuje, že rozložení prodeje vstupenek je vlevo zkreslené. Pátek a sobota jsou dny s největším počtem prodaných vstupenek, 305 a 352. Největší počet vstupenek tak bývá prodán v sobotu, a to 352 vstupenek.