Usage-based Insurance

From Simulace.info
Revision as of 19:46, 12 June 2012 by Xbarr10 (talk | contribs) (→‎Předpoklady a omezení modelu)
Jump to: navigation, search

Pojištění vozidel: Chování trhu při zavedení možnosti „pay as you drive“ (usage-based insurance)

Definice problému

V některých zemích, například ve Velké Británii, umožňují pojišťovny alternativní model platby za povinné ručení, známý jako "Pay as You Go". Pokud se klient rozhodne tento model využít, je mu do automobilu nainstalován GPS tracker snímající veškeré použití vozidla. Na základě dat z tohoto trackeru je poté vypočtena výše pojistného: obvykle jako paušální částka (pronájem zařízení) + variabilní složka dle najetých kilometrů. Tento systém může být rozšířen o penalizaci rizikového chování (například jízdy v noci, uvažuje se i o alkoholtesteru jako součásti záznamového zařízení) či odlišné tarifikace různých typů vozovek.

Cílem semestrální práce je simulovat reakci trhu povinného ručení na zavedení možnosti platit pojištění za ujeté kilometry místo pevné částky. Výsledky budou zkoumány zejména s ohledem na dynamiku chování (jak dlouho trvá modelu přechod do nového rovnovážného stavu, zda dochází k prudkým výkyvům) a typ výsledného rovnovážného stavu (atraktoru).

Předpokládaně chování modelu

Možnosti platby za ujeté kilometry budou zpočátku využívat (zejména) majitelé vozidel s výrazně podprůměrnou ročně ujetou vzdáleností, tedy i nehodovostí. (kteří na současném systému prodělávají). Tím odčerpají peníze ze systému klasického pojištění, na což pojišťovny musí zareagovat zvednutím výše pojistného. Při vyšší ceně pojistného se platba za ujeté kilometry stane výhodnou pro více pojištěnců, kteří odčerpají další peníze atd.

Pro určité vstupní parametry bude výše naznačený cyklus trhem tlumen (a ve výsledném rovnovážném stavu budou existovat zároveň oba systémy pojištění, Při dostatečně nízké ceně PAYG však dojde ke změně atraktoru, trh nedokáže cyklus brzdit a všichni klienti (až na jednoho posledního) přejdou k novému systému pojistného.

Výzkumné problémy

Jakým způsobem závisí podíl PAYG pojištěnců (po ustálení) na fixní a variabilní částce pojistného (při ostatních parametrech neměnných)?

Jaký je průběh vývoje trhu (v čase) pro vybrané vstupní parametry?

Metoda

Pro určení vhodné metody byla provedena analýza dle otázek, které jsou součástí Agentology[1] metodologie:


Are there entities that can make decisions?

Ano, pojištěnci i pojišťovny.

Are there many kinds of decision-making entities or many kinds of decisions?

V simulaci existují dva, respektive tři (pokud uvažujeme každý typ pojišťovny samostatně) druhy subjektů. Rozhodnutí jsou poměrně jednoduchá, v případě pojištěnců jde o volbu mezi dvěma typy pojištění, u pojišťoven o stanovení ceny pojistného tak, aby vyhověly požadavkům zákona (Pojistitel je povinen stanovit výši pojistného tak, aby zabezpečil trvalou splnitelnost závazků vzniklých provozováním pojištění odpovědnosti a úhradu příspěvků Kanceláři) [2] a odolaly konkurenčním subjektům.

Does it look like the system will have dynamic characteristics (its former states influence the future states)?

Ano.

We do not feel a need to treat an overall behavior of the whole system on macro-level.

Pojišťovny se rozhodují na základě makro-dat, které lze ale jednoduše agregovat z dat o jednotlivých objektech.

Is it difficult to describe the whole situation as a process diagram or state-and-transition diagram?

Situaci lze zachytit jako state-and-transition diagram s poměrně mnoha prvky, ale málo vazbami.

Is it difficult to “count up” the entities into lump sums and then work solely with such amounts? It means, are there many different entities that we cannot treat together?

Při jistém zjednodušení modelu (zejména absolutní racionalita pojištěnců a abstrahování od elasticity poptávky, viz kapitola Předpoklady a omezení modelu) lze simulovat i s agregovanými daty. Pro některá navrhovaná rozšíření jsou tato omezení nepřijatelná, poté by byl pravděpodobně vhodnější agentní model.

Are spatial factors of the environment important for the simulation?

Ne


Na základě uvedených otázek byla jako vhodná metoda zvolena diskrétní simulace. Z odpovědí ale vyplývají i omezení, která je třeba respektovat v dalších fázích modelování.

Jako prostředí byl zvolen tabulkový kalkulátor MS Excel, zejména z důvodů jeho dostupnosti, známému prostředí, matematickým schopnostem, možnostem doprogramovat další potřebné funkce pomocí VBA a poměrně dobrým možnostem analýzy a prezentace dat.

Model

Předpoklady a omezení modelu

  • Rovnováha na trhu: Do uvedení možnosti platby PAYG je trh v dokonalé rovnováze. Vlivem konkurence pojišťovny negenerují zisk, vybrané pojistné přesně kryje náklady na úhradu pojistných událostí.
  • Absolutní racionalita pojištěnců: Pojištěnec se rozhoduje vždy pro variantu přinášející mu nejvyšší zisk. Nemá žádné transakční náklady, takže se ke změně pojištění rozhodne i ve chvíli, kdy je pro něj výhodnější jen o několik haléřů. Toto zjednodušení obvykle ve skutečnosti platí až v dlouhém čase. Toto omezení lze chápat také tak, že simulace dává odhad maximálního možného efektu, kterého zavedení pojištění při daných parametrech dosáhne.
  • Cenová diskriminace: Model abstrahuje od různých cen pro různé objemy motoru, "bonusu dobrého řidiče" apod. Ceny vyjadřují průměrnou hodnotu. Předpokládá se, že i při použití modelu PAYG bude cena odstupňována (například podle hmotnosti vozidla, objemu motoru) podobně jako klasického pojištění.
  • Počet vozidel, najetých km, nehodovost: se v čase simulace nemění.


  • Počet ujetých kilometrů na automobil: Rozložení je dáno Gamma rozdělením, jeho parametry budou v modelu odhadnuty na základě dostupných dat.
  • Doba trvání pojistných smluv: Pojistné smlouvy se uzavírají vždy na dobu určitou 12 měsíců. Objem smluv v čase je rozložen rovnoměrně, takže každý kalendářní měsíc sochází k uzavření jedné dvanáctiny z celkového objemu pojistných smluv.

Relevantní data

něco [3] znovu [4]

Implementace

Simulace je provedena v prostředí MS Excel jako sled iterativně prováděných diskrétních operací, prováděných jednou za měsíc.

Konstanty (vstupní data) modelu

Model pracuje s následujícími konstantami (vstupními parametry):

Zkratka Název Hodnota (dle reálných dat) Poznámka
aut Počet vozidel 4435000
kmrocne_prumer Průměrný počet ročně najetých kilometrů na 1 vozidlo 9570 Jedna z vstupních hodnot pro parametry Gamma rozdělení
kmrocne_rozptyl Rozptyl ročně najetých km na vozidlo Jedna z vstupních hodnot pro parametry Gamma rozdělení, data nedostupná, použit kvalifikovaný odhad 200000 (odpovídá směrodatné odchylce 4472km)
Pojistné klasické Klasické roční pojistné za jeden automobil, počáteční hodnota
Pojistné PAYD - fixní část Fixní část PAYD pojistného, roční paušální platba za automobil
Pojistné PAYD - variabilní část Variabilní část PAYD pojistného: platba za ujetý kilometr

Proměnné modelu

Pro každé období se sleduje 12 proměnných, způsob jejich výpočtu je naznačen v následující tabulce:

Zkratka Název Vstupní hodnota Výpočet Poznámka
Období 1 i
Pojištěnců klasických
Pojištěnců PAYD
Pojistné klasické (rok)
Kilometrů klas
Kilometrů PAYD 0 Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \operatorname{kmpayd}(i) = \int_0^{pojistencupayd(i)} F(pojistencupayd(i)) } do 12. měsíce (zahřívací období) = 0
Pojistné vybrané klas
Pojistné vybrané PAYD - fixní složka
Pojistné vybrané PAYD - variabilní složka
Pojistné PAYD celkem
Pojistné celkem
Mezní km
Roční vybrané pojistné (klouzavý součet)

Funkce

najetychkm(hranicniprocento)

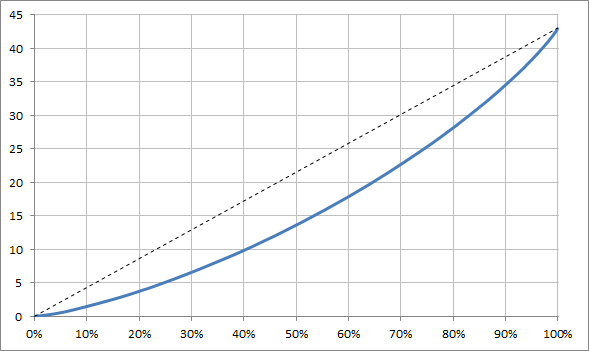
Funkce vrací počet kilometrů, které ročně souhrnně najede skupina nejméně jezdících automobilů (hranice je dána parametrem hranicniprocento). Jde o integrál kumulativní distribuční funkce gama rozdělení (s parametry danými konstantami Alpha a Beta), vynásobený počtem celkově najetých kilometrů (počet automobilů * průměr najetých kilometrů na automobil) 

Public Function najetychkm(hranicniprocento)
'najetychkm = hranicniprocento
If (hranicniprocento <= 0.995) Then
i = 2
Do While Worksheets(2).Cells(i, 1) <= hranicniprocento
i = i + 1
Loop
'najetychkm = Worksheets(2).Cells(i - 1, 4)
najetychkm = (Worksheets(2).Cells(i, 4) * (hranicniprocento - Worksheets(2).Cells(i - 1, 1)) + Worksheets(2).Cells(i - 1, 4) * (Worksheets(2).Cells(i, 1) - hranicniprocento)) / (Worksheets(2).Cells(i, 1) - Worksheets(2).Cells(i - 1, 1))
Else
najetychkm = Range("aut").Value * Range("kmrocne_prumer").Value / 12
End If
End Function

Integrál je počítán numericky jako plocha pod křivkou. Pro urychlení výpočtu a zjednodušení kódu je pro každý krok o konstantní velikosti 1% (lze použít libovolný krok) spočítán na druhém listu tabulky. Makro tedy pouze za pomoci cyklu nalezne dvě nejbližší vypočítané hodnoty, ze kterých vypočítá vážený průměr.

Kumulativní distribuce najetých kilometrů
Kumulativní distribuce najetých kilometrů [biliony km] (význam grafu je podobný jako u Lorenzovy křivky, tedy například 40% nejméně jezdících aut najede v součtu 10bio km. Přerušovaná čára ukazuje podobu grafu pro rovnoměrné rozdělení.)

Uživatelské rozhraní

Možná rozšíření

Výsledky

Závěr

Kód

Reference

  1. ↑ Šalamon, 2011, pg. 112-113
  2. ↑ 168/1999 Sb., § 3b
  3. ↑ Perry's Handbook, Sixth Edition, McGraw-Hill Co., 1984.
  4. ↑ Klein, Ernest, A comprehensive etymological dictionary of the English language, Vol II, Elsevier publishing company, Amsterdam, 1969, p.1317

Seznam literatury

  • (BRŮHOVÁ-FOLTÝNOVÁ, 2007) BRŮHOVÁ-FOLTÝNOVÁ, Hana. Centrum pro otázky životního prostředí, UK v Praze. Analýza každodenního dopravního chování dospělého městského obyvatelstva a nástroje regulace dopravy: Přehledová studie: Rešerše literatury 2.1. Praha, 2007. Dostupné z: http://www.czp.cuni.cz
  • (Eurostat, 2012) EUROSTAT. Passenger cars, by age [online]. 06-03-2012. [cit. 2012-05-30].
  • (OECD, 2010) OECD. IRTAD Annual Report 2009. 2010.
  • (Šalamon, 2011)
  • (168/1999 Sb.) 168/1999 Sb.: Zákon o pojištění odpovědnosti za škodu způsobenou provozem vozidla a o změně některých souvisejících zákonů. In: 57/1999. Dostupné z: http://portal.gov.cz/app/zakony
Retrieved from "http://www.simulace.info/index.php?title=Usage-based_Insurance/cs&oldid=875"