Multistage Games/cs
Contents
Úvod
Pojmem vícekolové hry rozumíme situaci, kdy stejní hráči hrají postupně Jednorázové hry, kde reagují na výsledek hry předchozí. Hráči dle výsledku předchozích her rozhodují o svých následujících tazích.
Vícekolové hry patří mezi hry v rozšířené formě, kdy hráči rozhodují konfliktní situaci po tazích. Rozhodnutí jednoho hráče o volbě jeho strategie ovlivňují předchozí tahy ostatních hráčů. Celá hra je procesem sekvence rozhodnutí jednotlivých hráčů.[1]
Definice
(1) V každém kole Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k} znají všichni hráči všechny tahy, provedené v předchozích kolech, (2) každý hráč má v každém z kol nanejvýš jeden tah a (3) žádná z informačních sad pro právě hrané kolo nepopisuje plánované tahy jednotlivých hráčů.
Vícekolová hra je konečná posloupnost jednorázových her, kde každá z nich je hra s úplnou ale nedokonalou informací. Tyto hry jsou hrány postupně stejnými hráči a celkový zisk je určen dle výsledků jednotlivých her. Je zde předpoklad, že každá hra je hrána v odlišnou dobu, tedy že hra č.1 je hrána v době č.1, hra č.2 v době č.2, atd. Předpokladem také je, že výsledek každé hry je znám všem hráčům.[2]
Je důležité si uvědomit, že hráči, když vědí, že bude následovat další hra, mohou plánovat a podmínit si své tahy v budoucích hrát na základě výsledků aktuální hry či na základě výsledků již proběhlých her.
Základní předpoklady
U každé hry v rozšířené formě bychom si měli ujasnit určité okolnosti dané hry a vícekolové hry nejsou výjimkou.
Jedná se o:
- Hráče,
- kdy je hráč na tahu,
- jaké má hráč možnosti při každém svém tahu,
- co hráč ví/zná při každém svém tahu,
- zisk, který je možné získat při jakékoliv kombinaci tahů.
Vyjasnění si těchto bodů nám pomůže lépe porozumět každé hře.
Typy
Vícekolové hry s pozorovanými akcemi
Předpokladem této hry je, že každý hráč zná historii předešlých kol.
Parametry pro každé kolo:
- počet hráčů: i=1..n
- aktuální kolo: k = 1..n
- historie předešlého kola: h0..hn
1) Hra začíná v kole k=1. Žádné předešlé kolo, na které bychom navazovali neexistuje, a historie h0 je tedy rovna nule. Jednotliví hráči provedou své tahy a kolo končí. Výsledek tohoto kola si zapíšeme jako h1, což je vstup pro navazující kolo.
2) Ve druhém kole (k=2) hráči znovu provedou své tahy, tentokrát jsou ale jejich tahy ovlivněny výsledkem kola předchozího (h1). V závislosti na historii je hra ukončena nebo pokračuje dalším kolem. Výsledek kola je označen jako h2.
3) Hra pokračuje až do kola k=n.
Historie hn, po které již nenásleduje další kolo, se nazývá ukončovací historie (terminal history).
Vícekolové hry s dokonalou informací
V případě této hry provádí svůj tah v každém kole pouze jediný hráč. I zde je předpokladem, že každý hráč zná historii předešlých kol.
1) Hra začíná v kole k=1. Hráč č.1 provede tah a toto kolo končí.
2) V kole k=2 hraje hráč č.2, který provede svůj tah. Tento tah může ale i nemusí reagovat na výsledek předchozího kola, kdy hrál hráč č.1. Pokud toto kolo není poslední, hra pokračuje dalším kolem, kdy hraje opět hráč č.1.
Pokud u této hry známe počet kol, je zde možné vytvořit strategii na základě zpětné indukce, kdy analyzujeme hru zpětně od nejlepšího možného tahu posledního hráče. Na základě zpětné indukce je také možné určit Nashovu rovnováhu vícekolové hry.[3]
Ukázka hry
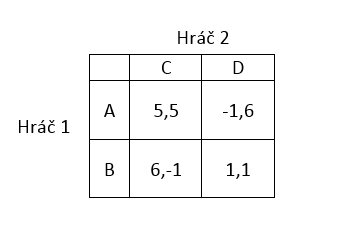
Mějme dva hráče, kteří hrají hru typu vězňovo dilema. Každý z hráčů tedy může buď mluvit a přiznat se (B,D), nebo zapírat a spoléhat na to, že druhý hráč udělá to samé (A,C).
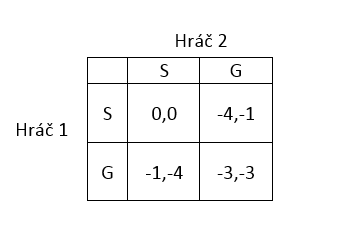
Po dohrání této hry (a odpykání si patřičných let) se oba hráči dostávají do možnosti odplaty a ocitnout v situaci, kdy každý z nich se může přidat do gangu (G) nebo zůstat sám (S). Situace je znázorněna v následující matici.
Pokud oba hráči zvolí S, tak bez ohledu na výsledek předešlé hry si každý půjde svou cestou, a zisk obou je 0. Pokud oba vstoupí do gangu (G), budou spolu bojovat, utrží ztrátu a jejich výsledný zisk bude -3. Třetí situace je, když jeden z hráčů zvolí vstup do gangu (G) a druhý zůstane sám (S). Ten co bude sám se neubrání a utrpí velkou ztrátu -4. Druhý hráč, který se stal součástí gangu, je pouze mírně zraněn, a jeho zisk z této hry je -1.
Pokud budeme každou z výše uvedených her hrát samostatně, hráči nebudou hry brát v souvislostech a budou se snažit v každé dosáhnout nejlepšího výsledku. Pokud ale hráč ví, že hry budou na sebe navazovat, má možnost vytvořit si strategii a chovat se podle toho.
Vezměme si hráče 1. Hráč 1 se rozhodne, že v 1. hře bude hrát B (mluvit) a ve 2. hře bude hrát S (sám) pouze v tom případě, pokud hráč 2 bude v první hře hrát C (zapírat). V tomto případě by hráč 1 měl z první hry zisk 6 a z druhé hry 0.
Pokud ale hráč 2 v první hře bude mluvit (D), hráč 1 má naplánováno, že v druhé hře bude hrát G (gang).
Tuto strategii lze obecně zapsat takto:
Pokud se ve hře 1,2, ..., t−1 stane to a to, pak ve hře t zvolím akci a.
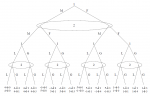
Pokud se podíváme znovu na první hru, tak tato hra má čtyři možné výsledky. Každý hráč by měl mít naplánovanou strategii pro další hru pro každý z těchto výsledků, protože nikdy neví, jak bude hrát protihráč. Všechny možné situace je dobré znázornit např. pomocí stromového grafu.
Celkový získ
Při určení celkového zisku vícekolové hry je nutné počítat s během času a s očekávaným snižováním hodnoty zisku budoucí hry (která se bude konat např. za rok nebo se nemusí konat vůbec) oproti hře, konané dříve. Celkový zisk se počítá obdobně, jako výpočet současné hodnoty v podnikové ekonomice.[2]
Vezměme příklad, kdy máme dvě hry, jedna byla hrána dnes a druhá až za dva roky. Zisk z obou her je stejný, např. 10. Hodnota zisku z druhé hry je ale nižší než ze hry, hrané dnes, protože aktuální zisk má pro nás větší hodnotu. Pokud budeme brát, že zisk jsou peněžní prostředky, tak dnes je můžeme investovat (např. uložit na vkladový účet) a do zítřka nám přinesou výnos (úrok). Budoucí zisk je nižší právě o tento získaný úrok.[3]
Druhou možností odůvodnění snížení hodnoty budoucího zisku je pravděpodobnost konání budoucí hry. Nikdy si nemůžeme být 100% jisti, že se další hra bude konat. Zisk z první hry je spolehlivější a má větší hodnotu, než zisk z druhé hry, u které je určitá pravděpodobnost, že se nebude konat (a tedy nezískáme žádný zisk/peníze).
Dokonalé rovnováha podher (Subgame Perfect Equilibrium)
Definice:
Sada strategií ve vícekolové hře s pozorovanými akcemi má dokonalou rovnováhu podher, pokud obsahuje Nashovu rovnováhu v každé podhře originální hry.[3]
Zdroje
- ↑ DLOUHÝ, Martin; FIALA, Petr. Úvod do teorie her. 2.přepracované vydání. Vysoká škola ekonomická v Praze : Nakladatelství Oeconomica, 2009. 120 s. ISBN 978-80-245-1609-7.
- ↑ 2.0 2.1 Tadelis, Steve. Game Theory: An Introduction. Princeton: Princeton UP, 2013. Print. http://faculty.haas.berkeley.edu/stadelis/Game%20Theory/econ160_week5.pdf
- ↑ 3.0 3.1 3.2 https://wwz.unibas.ch/fileadmin/wwz/redaktion/witheo/personen/georg/for_lectures/games_3_10_netz.pdf Cite error: Invalid
<ref>tag; name "" defined multiple times with different content Cite error: Invalid<ref>tag; name "" defined multiple times with different content - ↑ Multistage_Games