Nash equilibrium

Nash equilibrium is a fundamental concept in the game theory defined by John Nash in 1950s and it is highly used method of predicting the outcome of a strategic interaction in the social sciences.

Games in strategic form

To define Nash equilibrium, we have to define one of the most widely used mathematical model of game theory, game in strategic (also called normal) form. Game in the strategic form is a model of interacting decision-makers. In the game theory, the decision-makers are very often called players. Each player in the strategic game has a set of possible actions and preferences about the action profile, which is list of all possible actions of all players. You can find more about strategic or normal form at Normal form page.

To define it more precisely, strategic game consist of:

• a set of players i
• for each player, a set of actions (or strategies) a
• for each player, preferences (or payoffs) over the set of action profiles

Definition of Nash equilibrium

Now We can define Nash equilibrium as an action profile a* with the property that no player i can do better by choosing an action different from 'a*i , given that every other player j adheres to a*j .

In own words, Nash equilibrium is such solution, that you cannot do any better by choosing different one.

Now we know, what Nash equilibrium is, so let´s find out, how to find it.

Nash equilibrium and zero sum games

Zero sum games are games in the game theory, where one player loses what second wins or vice versa. It is one of the simplest game model. It could be represented by payoff matrix (or we can say table) like this one below.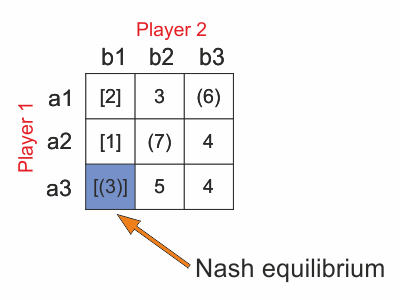
In this matrix ai are actions of player 1 and bi are actions of player 2. Numbers inside the matrix are payoffs of player 1 in case of selected actions. To find Nash equilibrium, we have to find steady state first. In zero sum games, the steady state is the element in the payoff matrix, which is the highest in the column and also the smallest in the row. This is because second player tries to minimize payoff of player 1, because first player payoff is -(payoff ) of second player. DLOUHY In our matrix, we found the steady state (element 3). It means that this game represented by payoff matrix has pure Nash equilibrium, which is action pair (a3,b1). So the Player 1 will choose action a3 and Player 2 action b1. There could be more steady states in the game represented by matrix, or none. Does it mean, that there is no Nash equilibrium? Not really. If there is not steady state, than the game doesn´t have pure Nash equilibrium but Nash equilibrium is in mixed strategies. In case of more steady states than one with same value, the game has alternative Nash equilibria. DLOUHY We will find out more about mixed strategies after a while. Now let´s do some practise exercise 1

Find steady state and pure Nash equilibrium if there is any.

Fill in the payoffs into the matrix a) so as game has one steady state and pure Nash equilibrium b) so as game has more than one steady state and has alternative Nash equilibria

Mixed strategies As mentioned above if we cannot determine steady state, than there is no pure Nash equilibrium but Nash equilibrium is in mixed strategies. That means that we cannot precisely determine which actions will players choose but we can identify probability distribution over player´s actions (strategies). Generally speaking, we can define probability, that player one or two will choose the action. To determine this probability distribution is more complicated. At first, we have to solve maximization task using linear programming methods:

maximize: q1 +q2+.....+qn s.t. a11*q1+a12*q2+.....+a1n*qn <=1 ... ... am1*q1+am2*q2+.....+amn*qn <=1 qj>=0; j=1,2,....,n where q1...qn are variables and a11...amn are individual payoffs for combination of actions. This task can be solved using Excel, Lingo or manually by simplex method.

• notes*

To get Nash equilibrium in mixed strategies, we can also solve dual linear task, which is related to the maximization task listed above. Because results are equivalent and to solve dual task is more complicated, only primal task is demonstrated. If you are interested, you can find more about linear programming at http://en.wikipedia.org/wiki/Linear_programming#Duality Non zero sum game and Nash equilibrium Non zero sum game are little bit more complex than zero sum games. Unlike the zero sum games, payoffs of one player are not dependent on second player´s payoffs. That means Players try to maximize their own profit. As a mathematical representation of this kind of game, we can also use matrix. But this matrix is little bit different, because there are payoffs of both players in it. The first number in the cell is payoff of Player 1 and the second one is payoff of Player 2. To determine Nash equilibrium, we have to find maximum value in the columns for first player and maximum value in the rows for second player. This is because both players try to maximize their profit based on second player´s choice. DLOUHY In this matrix, we can find one pure Nash equilibrium, which is action pair (a3, b1). As same as in zero sum game, there are three possibilities, that may occur. We can determine one pure Nash equilibrium, more than one or none. If there is more than one Nash equilibrium and one of them dominates (either payoffs are higher (or one payoff is the same) then payoffs in other Nash equilibrium) others, than players will choose this solution, because is better for both players. If there is more than one Nash equilibrium and no one of them dominates others, than we can´t determine solution to choose. The last possibility is that there is no pure Nash equilibrium in the game. In this case, we have to find Nash equilibrium in mixed strategies. exercise 2 Find pure Nash equilibrium if there is any.

Nash Equilibrium decision problems Sometimes things aren´t so clear and Nash equilibrium didn´t get sufficient solution in strategic games, so let´s show some examples of well-known strategic games. Prisoner´s dilemma The Prisoner's Dilemma is one of the most well-known strategic games. It was researched many times and many ways due to huge variety of situations in real life which is similar to this problem. The definition of Prisoner´s dilemma There are two suspects in a major crime situated in separate cells. We have enough evidence to convict each of them of a minor offense, but we can´t convict either of them of the major crime unless one of them pleads guilty and tells information that help to find the second one guilty. If they both say nothing (cooperate), each will be convicted of the minor offense and spend one year in jail. If one and only one of them betrays other, than he will be set free and used as a witness. The other one will spend four years in jail. If they both betray, they will spend three years in jail. NASH

We can demonstrate this situation as shown above. Payoffs in the matrix represent years in prison (higher values are worse). When we try to find Nash equilibrium, we get pair of action (betray,betray), but as we can see that isn´t the best solution. The Best solution is (cooperate, cooperate). This example shows, that Nash equilibrium is not always Pareto-effective. Bach or Stravinsky (also known as battle of sexes) Two people decided to go out together to a concert of music by either Bach or Stravinsky. However, one person prefers Stravinsky and the other person prefers Bach. The situation is represented using payoff matrix below. CANETTI Battle of sexes represent situation, when two people want to spend time together, but they have different preferences. In this case we found two Nash equilibria, but we still don´t know how to play. Either of them will have to yield.

Coordination game Now imagine almost same situation as above, but they both prefer Bach to Stravinsky. Situation is listed below. In this situation we get also two Nash equilibria and one (Bach, Bach) is noticeably better than other, but notion of Nash equilibrium doesn´t eliminate the second one (Stravinsky, Stravinsky) .

references