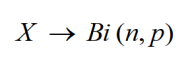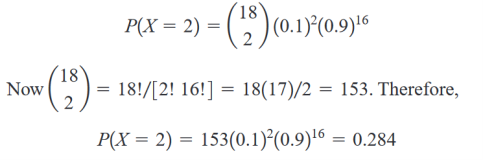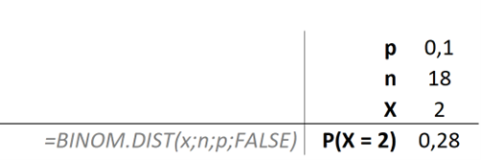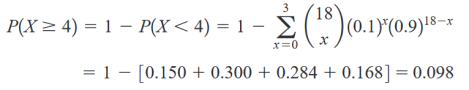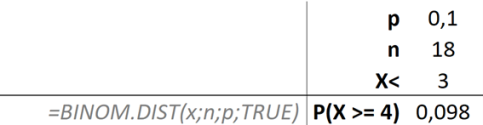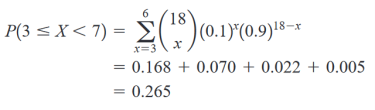Binomické rozdělení

Přemýšleli jste někdy o tom, jak předpovědět počet úspěchů v sérii nezávislých pokusů? Nebo jste možná zvědaví na pravděpodobnost dosažení konkrétního výsledku v sekvenci otázek s odpověďmi ano/ne? Pokud ano, hovoříme v podstatě o binomickém rozdělení, které se vztahuje k binomickým experimentům (tj. s binárními výsledky). Binomické rozdělení je důležitým konceptem v oblasti datové vědy a často se používá v rámci podnikových aplikací.

Úvod

Pravděpodobnostní rozdělení pro experiment s mincí. Počet pokusů = 10 a pravděpodobností úspěchu (pád orla při jedném hodu) = 0,5.

Přemýšlejme o následujících experimentech a náhodných veličinách:

1. Házíme 10krát mincí. Označme počet kolikrát padne orel.
2. Stroj vyrábí díly a některé z nich jsou vadné. Označme jako počet vadných dílů ze 100 z nich náhodně vybraných.
3. Z celkového počtu pacientů trpících konkrétním onemocněním 35 % zažije zlepšení díky určitému léku. U následujících 1000 pacientů, kterým je podán ten samý lék, označme jako počet pacientů, kteří zpozorují zlepšení.
4. Test obsahuje 10 otázek s více možnými odpověďmi, každá s čtyřmi možnostmi, a vy hádáte u každé otázky. Označme jako počet správně zodpovězených otázek.

Každý z těchto náhodných experimentů si lze představit jako soubor opakovaných náhodných pokusů: 10 hodů mincí nebo třeba 1000 pacientů užívajících lék. Náhodná veličina je počet pokusů, které splňují určité kritérium. Výsledek každého pokusu buď splňuje kritérium, nebo ne; proto lze každý pokus shrnout jako „úspěch“ nebo „neúspěch“. Například v experimentu s testem je pro každou otázku pouze jedna kombinace možností, která je správná, a tedy považována za úspěch.

Termíny „úspěch“ a „neúspěch“ jsou pouze označení. V případě experimentu 2 je vyrobení vadného dílu označováno jako „úspěch“, protože počítá vadné díly. Stejně dobře můžeme použít označení „A“ a „B“ nebo „0“ a „1“.

Terminologie

Binomický experiment

Nebo také Bernoulliho experiment/Bernoulliho schéma jsme si v úvodu představili, pojďme si ho nadefinovat a formalizovat.

Požadavky

Požadavky pro to, aby náhodný experiment byl binomickým experimentem, jsou následující:

• Pevný počet (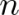) pokusů.
• Každý pokus musí být nezávislý na ostatních. (výsledek jednoho pokusu nemá žádný vliv na výsledek ostatních pokusů.)
• Každý pokus má právě dva možné výsledky, nazývané "úspěch" (výsledek, který nás zajímá) a "neúspěch".
• Existuje konstantní pravděpodobnost (pravděpodobnost, že pokus skončí „úspěchem“, je stejná v každém z pokusů) (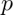) úspěchu pro každý pokus, přičemž doplňkem této pravděpodobnosti je pravděpodobnost „neúspěchu“, která se někdy označuje jako .

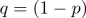Náhodná veličina

Pro definici binomického rozdělení začneme s definicí náhodné veličiny . Tu lze jednoduše definovat jako číselné vyjádření výsledku náhodného jevu.

Binomická náhodná veličina

V binomických náhodných experimentech je počet „úspěchů“ v n pokusech náhodný. Může nabývat celočíselných hodnot od 0, pokud všechny pokusy skončí „neúspěchem“, nebo může být tak vysoký jako je , pokud všechny pokusy skončí „úspěchem“. Náhodná proměnná , která reprezentuje počet „úspěchů“ v těchto pokusech, se nazývá binomická náhodná veličina a je určena hodnotami a .

Definice

Binomická náhodná veličina je definována jako počet výskytu události (úspěchů) v Bernoulliho pokusech. To, že má náhodná veličina binomické rozdělení zapisujeme:

Příklad: Binomické nebo ne?

Zvažme ještě několik náhodných experimentů. U každého z nich rozhodneme, zda je náhodná proměnná binomická. Pokud je, určíme hodnoty pro a . Pokud není, vysvětlíme proč.

Příklad A

Házíme spravedlivou kostkou 50krát; je počet krát, kdy padla šestka.

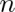je binomická s = 50 a 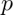= 1/6.

Příklad B

Opět házíme spravedlivou kostkou, je počet hodů potřebných k dosažení šestky.

není binomická, protože počet pokusů není pevně stanovený.

Příklad C

Vybíráme náhodně 3 karty jednu po druhé, nevracíme je zpátky do balíčku, z klasické sady obsahující 4 druhy karet. je počet vybraných karet se znakem srdce.

není binomická, protože výběry nejsou nezávislé. (Pravděpodobnost úspěchu (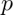) není konstantní, protože je ovlivněna předchozími výběry.)

Příklad D

Odpovídáme na 10 testových otázek zcela náhodně, prvních pět otázek je ano/ne a druhých pět otázek má čtyři možnosti, ze kterých je jedna správná. představuje počet správných odpovědí.

není binomická, protože pravděpodobnost 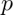se mění z 1/2 na 1/4.

Příklad E

Pravděpodobnost mít krevní skupinu B je 0,1. Vybíráme 4 náhodné osoby. je počet osob s krevní skupinou B.

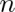je binomická s = 4 a 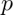= 0,1.

Komentář: Při výběru relativně malé náhodné vzorky (4 osoby) z velké populace, i když se odběr provádí bez „náhrady“, můžeme předpokládat nezávislost, protože matematický vliv odstranění jednoho jedince z velké populace na další výběr je zanedbatelný.

Binomické pravděpodobnostní rozdělení

Nyní je čas diskutovat o pravděpodobnostním rozdělení binomické náhodné veličiny. Začneme jednoduchým příkladem a poté se přesuneme k obecnému vzorci.

Příklad Přenosový kanál

Mějme digitální přenosový kanál, který přenáší 4 bitový signál. Pokusy o přenos jsou nezávislé. Šance, že se jeden bit, který je přenesen přes kanál, přenese s chybou je 0,1. Nechť je označuje počet bitů s chybou. Určeme .

• Použijme písmeno E pro označení bitu s chybou a písmeno O pro označení bitu bez chyby, tedy přijatého správně. Výsledky tohoto můžeme reprezentovat jako seznam čtyř písmen, která označují bity s chybou a bity bez chyby. Například výsledek OEOE znamená, že druhý a čtvrtý bit jsou s chybou a ostatní dva bity jsou bez chyby. Příslušné hodnoty tedy jsou:

Výsledek přenosu	x	Výsledek přenosu	x
OOOO	0	OEOE	2
OOOE	1	EOEO	2
OOEO	1	EOOE	2
OEOO	1	OEEE	3
EOOO	1	EOEE	3
OOEE	2	EEEO	3
OEEO	2	EEOE	3
EEOO	2	EEEE	4

• Pro = 2 je tedy možných 6 výsledků přenosu: {OOEE, OEEO, EEOO, OEOE, EOEO, EOOE}
• Za předpokladu, že jsou pokusy o přenos jednoho bitu nezávislé, je pravděpodobnost možnosti {EEOO}:

• Také platí, že každý z šesti výsledků, kde =2, má stejnou pravděpodobnost výskytu a proto

Nebo všeobecně: = počet možných „úspěšných“ výsledků pro x chyb * pravděpodobnost každé „úspěšné“ možnosti s výsledkem x chyb a délkou 4

• Pro jednoduší odvození můžeme vytvořit tabulku pravděpodobností:

• Všimneme si vlastnosti v tabulce:

Můžeme zevšeobecnit na: pravděpodobnost každé „úspěšné“ možnosti s výsledkem

• Ještě nám zbývá odvodit část počet možných „úspěšných“ výsledků pro x, která není na první pohled tak intuitivní. Po krátkém zamyšlení je ale jasné, že se jedná o jednoduchou kombinaci, kdy z množiny 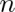objektů vybíráme počet objektů (x), přičemž nám nezáleží na pořadí. Tedy:

Definice

Formalizujme tedy uvedené informace do definice binomického rozdělení:

Podmínky

Náhodný experiment se skládá z Bernoulliho experimentů tak, že:

1. Každý experiment je nezávislý
2. Každý experiment má právě dva možné výsledky – „úspěch“ a „neúspěch“
3. Pravděpodobnost „úspěchu“, označována 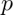, pro každý pokus, zůstává konstantní

Vzorec

Náhodná proměnná , která udává počet pokusů s „úspěchem“, má binomické rozdělení s parametry 0<<1 a = 1, 2, … Pravděpodobnostní funkce proměnné je dána následovně:

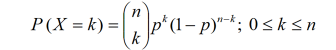
Charakteristiky rozdělení

Pro odvození střední hodnoty opět využijeme intuitivního příkladu: Jak nám je již známo, pravděpodobnost mít krevní skupinu typu B je 0,1. Nebo tedy jinými slovy, zhruba 10 % populace má krevní skupinu B. Předpokládejme, že náhodně vybereme 120 lidí. Kolik lidí můžeme očekávat, že bude mít krevní skupinu typu B? Odpověď, 12, se zdá být zřejmá. Automaticky jsme vynásobili počet lidí - 120, pravděpodobností výskytu krevního typu B – 0,1. Z toho jednoduchého příkladu můžeme začít odvozovat.

Střední hodnota

Pokud je binomická náhodná veličina s parametry a , pak střední hodnota (očekávaná hodnota) je:

Rozptyl

Rozptyl je na odvození méně intuitivní, ale ne nemožný. Nicméně je tato problematika odvození mimo rámec této kapitoly, a proto ho uvedeme jenom jako vzorec:

Pro příklad s krví by to tedy znamenalo:

V náhodném vzorku 120 lidí bychom očekávali přibližně 12 osob s krevním typem B, s odchylkou přibližně 3,3.

Příklady

Modelový příklad - znečištění vody

Zadání

Každý vzorek vody má 10% šanci obsahovat určitý objem znečišťujících látek. Předpokládejme, že vzorky jsou nezávislé s ohledem na přítomnost znečišťující látky.

Otázky

Spočítejte pravděpodobnost, že v následujících 18 vzorcích budou právě 2 vzorky obsahovat znečišťující látku.

Nechť X představuje počet vzorků obsahujících znečišťující látku z 18 analyzovaných vzorků. Potom X je binomická náhodná veličina s parametry p = 0.1 a n = 18.

Případně použití excelu:

Spočítejte pravděpodobnost, že alespoň čtyři vzorky obsahují znečišťující látku.

Z důvodu jednoduššího výpočtu využijeme raději komplementární pravděpodobnost k pravděpodobnosti P(X≥4).

Případně použití excelu:

Spočítejte pravděpodobnost, že vzorek bude obsahovat 3 nebo víc znečišťujících látek a zároveň míň než 7

Případně použití excelu:

Příklad reálné aplikace

Zadání

Po všech definicích se zaměříme na reálnou aplikaci pomocí příkladu s letenkami.

Stude ukázaly, že ze všech rezervací se k letu skutečně dostaví 90 % pasažérů. Předpokládejme, že malý přepravní letoun má 45 sedadel. Budeme předpokládat, že pasažéři přicházejí nezávisle na sobě (i když tato předpokládaná nezávislost není zcela přesná, protože ne všichni cestují sami, ale pro účely našeho experimentu ji použijeme).

Často se stává, že letecké společnosti pro let prodá víc letenek, než je ve skutečnosti v letadle sedadel. Dělají to proto, aby eliminovali počet neobsazených sedadel, pokud se někteří pasažéři nedostaví. Nicméně, pokud se rozhodnou přeobsadit let, vystavují se riziku, že budou mít více pasažérů než sedadel a někteří pasažéři mohou být nespokojeni. Společnost také musí nést dodatečné náklady spojené s přeřazením těchto pasažérů na jiný let a případně jim poskytnout ubytování.

S ohledem na tato rizika se letecká společnost i tak rozhodne prodat více než 45 letenek. Pokud chtějí udržet pravděpodobnost, že na let dorazí více než 45 cestujících, na méně než 0.05, kolik lístků by měli prodat?

Řešení

Jedná se o binomickou náhodnou proměnnou, která představuje počet cestujících, kteří se dostaví na let.

Máme hodnotu p = 0,90 a n musíme určit.

Pro n budeme uvažovat o hodnotách n>45.

V zadaní máme zadánu pravděpodobnost pro „chybějící“ pasažéry P(X ≤ 45). My budeme chtít znát ale pravděpodobnosti P(X > 45), co můžeme napsat jako 1 – P(X ≤ 45)

Pro výpočet si pomůžeme Excelem: Hodnota „TRUE“ ve vzorci pro pravděpodobnost „X ≤ 45“, TRUE znamená, že chceme získat součet pravděpodobností pro hodnoty od 0 do 45. Pokud bychom místo toho použili FALSE, funkce by vrátila pravděpodobnost přesně pro hodnotu 45, a ne součet pravděpodobností pro hodnoty menší nebo rovny 45.

Zanalyzujme si výsledky. Pokud letecká společnost prodá 50 lístků, bude pravděpodobnost, že na let dorazí více než 45 cestujících 0,43 co je rozhodně víc, než požadovaných 5 %.

Můžeme tím pádem dospět k závěru, že pokud společnost prodá 47 lístků, tak sníží pravděpodobnost, že se dostaví víc než 45 cestujících na 4 %, co je míň než požadovaných 5 %.

Zajímavé fakty

• Švýcarský matematik Jakob Bernoulli (1655-1705) buď nebyl spokojen se svými výsledky, nebo nenašel vhodné aplikace pro širší využití svých teorií, a proto na knize, kde se objevil důkaz patrně od roku 1692 nepracoval. Vyšla až posmrtně v roce 1713.

• V roce 1936 britský statistik Ronald Fisher využil binomického rozdělení k publikaci důkazů možné vědecké manipulace - ve slavných experimentech s genetikou hrachu, které popsal rakouský botanik Gregor Mendel v roce 1866. Fisher zpozoroval, že Mendelovy zákony dědičnosti by diktovaly, že počet žlutých hrachových zrn v jednom z Mendelových experimentů bude mít binomické rozdělení s n = 8023 a p = 3/4, což by dávalo průměr np ≅ 6 017 žlutých zrn. Fisher zjistil pozoruhodnou shodu mezi tímto číslem a Mendelovými daty, které ukázaly 6 022 žlutých zrn ze 8 023. Očekávalo by se, že číslo bude blízké, ale taková blízkost by se měla vyskytovat jen 1 z 10krát. Fisher navíc zjistil, že všechny ze sedmi výsledků Mendelových pokusů s hrachem byly extrémně blízké očekávaným hodnotám, dokonce i v jednom případě, kdy Mendelovy výpočty obsahovaly drobnou chybu. Fisherova analýza vyvolala dlouhotrvající kontroverzi, která zůstává dodnes nevyřešena.

• Jak už bylo na příkladech uvedeno, binomické rozdělení se používá v inženýrství, biologií a medicíně. Nalezneme ho také v psychologii, kde ho lze použít k modelování počtu správných odpovědí v paměťovém testu nebo počtu lidí, kteří preferují určitý podnět před jiným. Ve společenských vědách, demografii a politologii lze binomické rozdělení použít k modelování počtu voličů, kteří podporují určitého kandidáta, nebo počtu domácností, které vlastní určitý typ spotřebiče. A nebo třeba také v sociologii k modelování pravděpodobnosti, že určitý počet osob sleduje určitý televizní kanál na základě ano/ne dotazníku. Nebo si možná samy namodelujete počet spamu, který za den dostanete do emailu.