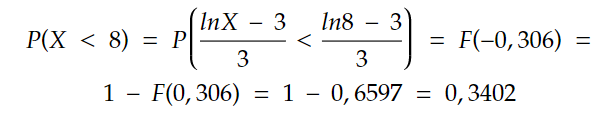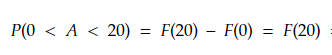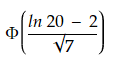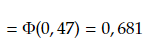Logaritmicko-normální rozdělení
Contents
Úvod
Logaritmicko-normální rozdělení, někdy také nazýváno Galtonovo rozdělení, je varianta normálního rozdělení. I jako u normálního rozdělení, se jedná o rozdělení spojité. Čím se však liší je, že na rozdíl od normálního rozdělení je logaritmicko-normální rozdělení asymetrické a zešikmené doleva. Tato šikmost umožňuje vyjadřovat přirozenou asymetričnost sady dat, kdy položky nejsou v uzavřeném intervalu, ale naopak v intervalu, který je z jedné strany neohraničený. [1] Používá např. extenzivně v modelech pro určování kvality produktu [2] nebo při modelování přijmů a platů.
Definice
Náhodná veličina X má logaritmicko-normální (lognormální) rozdělení s parametry μ a σ2, jestliže náhodná veličina ln X má normální rozdělení N(μ,σ2). [1]
Kde µ je střední hodnota a σ² je směrodatná odchylka. Střední hodnotou je definována jako součet všech hodnot náhodné proměnné x dělený počtem hodnot. Vypočtený průměr pak udává, jaká stejná část z úhrnu hodnot sledované číselné proměnné připadá na jednu jednotku souboru. [3] Směrodatná odchylka je odmocnina z rozptylu, který se definuje jako aritmetický průměr čtverců odchylek jednotlivých hodnot sledované proměnné x od průměru celého souboru. [4] Logaritmicko-normální rozdělení pak vypadá takto:

Zde je vidět v porovnání s normálním rozdělením níže, které není šikmé a je symetrické:

Vzorce
Hustota pravděpodobnosti: 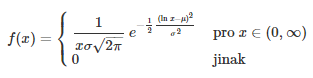 [1]
[1]
V grafu nabývá následujícího tvaru:

Distribuční funkce: 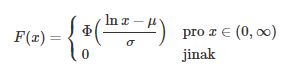 [1]
[1]
V grafu nabývá následujícího tvaru:

Reálné aplikace
Jak již bylo zmíněno výše, logaritmicko-normální rozdělení je na rozdíl od normálního rozdělení asymetrické a šikmé. Tyto vlastnosti však způsobují, že se toto rozdělení častěji svými jevy blíží realitě. Je to možné pozorovat v různých oborech, kde nachází široké využití.
Například ve financích a investování se používá velmi zběžně ke sledování růstu či poklesu cenných papírů. Neváže se to však jen na burzovní obchody, ale lze předpovídat zhodnocení jakékoliv komodity, ať už se jedná třeba o hodnotu nemovitosti, nebo cenu sběratelských předmětů. [9]

Často se také využívá jako ilustrace platového či mzdového rozdělení v populaci. Graf ilustruje mzdovou sféru ČR. Hned si lze všimnou, že průměr se nachází téměř u 3. kvartilu a mzdy se logaritmickou křivkou (proto se jedná o logaritmicko-normální rozdělení) blíží k vodorovné ose x. Tedy existuje minimální mzda, která značí ohraničení rozdělení z levé strany. Jak se mzda zvyšuje, tak stoupá i počet zaměstnanců s danou mzdou. Toto stoupání však brzo skončí a nadále platí, že čím více se zvyšuje mzda, tím menší je četnost zaměstnanců s takovou mzdou. Je však možné, že budou existovat i zaměstnanci s tak mzdou tak vysoké částky, že ne grafu již není. Právě díky nim je rozdělení ohraničeno pouze z jedné strany, a to minimální mzdou. Zatímco u normálního rozdělení jsou hodnoty mediánu, průměru a modu všechny totožné, zde je možné pozorovat značný rozdíl mezi mediánem a průměrem, kdy mediánem je téměř o 20% menší než průměr. Logaritmicko-normální rozdělení lze tedy využít pro většinu jevů, kdy je rozdělení z jedné strany ohraničeno.
Další příklad může být rozdělení nezbytného času pro nasazení přístroje pro dojení mléka.

Zde je možné pozorovat, že tento graf se daleko víc blíží k vzhledu normálního rozdělení, ale vzhledem k povaze dostupných dat byla velká variance operátorů, kteří nasazovali přístroje pro dojení krev déle než 20 sekundd, zatímco nejběžnější bylo nasadit přístroj kolem 10 sekund. Je tedy vidět, že samotná povaha dostupných dat (která může být ovlivněna poskytovatelem) má velký vliv na vyobrazení grafu. V tomto případě na to měl vliv i fakt, že velikost vzorku, tedy dat, byla relativně malá. [11]
Existuje velké množství aplikací pro logaritmicko-normálního rozdělení. Příklad těchto aplikací je:
- znázornění délky šachové hry [12]
- měření velikosti živé tkáně [13]
- rozdělení velikosti souborů obsahující zvukové či video stopy [14]
- rozdělení velikostí částic
- Gibratův zákon, také známý jako zákon proporcionálního účinku je prvním pokusem (1931) o to systematicky vysvětlit stochastickými termíny zkreslený vzorec distribuce velikosti firem v rámci odvětví. Jinak řečeno se analyzuje vztah mezi velikostí firmy a pevným růstem. [15]

Modelové příklady
1. Excel příklad
Mějme medián = 104Kč, směrodatnou odchylku = 20,4%. Zjistěte hustoty pravděpodobnosti v případě, že modus je 70Kč, 100Kč a 125Kč:
- Nejdříve je třeba připravit hodnoty pro vložení do excel funkce
- Medián vydělíme 100 a dostaneme 1,04, dále spočítáme logaritmus 1,04, což je 0,039
- Procento směrodatné odchylky vydělíme 100, bude tedy 0,204
- Připravíme mody stejně jako ostatní hodnoty, tedy vydělíme 100, hodnoty budou tedy 0,7, 1 a 1,25.
- Vložíme do funkce LOGNORM.DIST(x,střed_hodn,sm_odchylka,kumulativní), kde
- x je modus, tedy 0,7, 1 a 1,25
- střed_hodn je medián, tedy 0,039
- sm_odchylka je směrodatná odchylka, tedy 0,204
- protože chceme funkci hustoty pravděpodobnosti, vložíme NEPRAVDA
- V případě modu 70Kč je hustota pravděpodobnosti = 0,002
- V případě modu 100Kč je hustota pravděpodobnosti = 0,01
- V případě modu 125Kč je hustota pravděpodobnosti = 0,005
2. Excel příklad
Firma XY má průměrnou mzdu 50 000 Kč, jejíž směrodatná odchylka je 10 000 Kč. Zjistěte pravděpodobnost v 95% kvantilu:
- Nejdříve je třeba připravit hodnoty pro vložení do excel funkce
- Spočítáme logaritmus průměrné mzdy 50 000, což je 10,8197
- Směrodatná odchylka je 10 000, potřebujeme však získat procento a 10 000 z 50 000 je 20%. Toto procento dále vydělíme 100 a dostaneme 0,2
- Potřebujeme 95% kvantil, což pro nás bude 0,95 po vydělením 100
- Použijeme funkci LOGNORM.INV(pravděpodobnost; střed_hodn; sm_odch)
- pravděpodobnost je kvantil, tedy 0,95
- střed_hodn je logaritmus průměrné mzdy, tedy 10,8197
- sm_odchylka je směrodatná odchylka, tedy 0,2
- 95% kvantil je 69 471,42 Kč
1. Počítací příklad
Mějme hodnotu A, která je LN[3;5] s parametry μ a σ2
- Určete distribuční funkci pro hodnotu 8
- Jak je vidět na obrázku níže, v první řadě si do funkce dosadíme naše hodnoty. Vypočítáme "pravou stranu" a výsledek použijeme pro vyhledání kýžené hodnoty v tabulkách distribuční funkce normovaného normálního rozdělení. Tím, že jsme vypočítali logaritmy na začátku jsme z toho prakticky udělali normální rozdělení. Výsledek odečteme od 1 pro získání hodnotu distribuční funkce
- Určete medián
- Medián lze považovat za 50% kvantil a tak to budeme počítat. Podle tabulek normovaného rozdělení je 50% kvantil roven 0. Dosadíme se tedy do exponentu eulerova čísla naše hodnoty podle obrázku níže a dostaneme výsledek
- Určete 95% kvantil
- Postup je zde obdoný jako u zjišťování mediánu s rozdílem, že tentokrát hledáme 95% kvantil. Musíme se tedy podívat do tabulky pro kvantily normálního rozdělení, kde zjístíme, že 95% kvantil, tedy 0,95 má hodnotu 1,645. To dosadíme do vzorce (viz obrázek níže) a získáme výsledek
2. Počítací příklad Máme náhodnou veličinu A s logaritmicko-normálním rozdělením s parametry μ=2; σ2=7. Zjistěte, jaká je pravděpodobnost, že tato náhodná veličina A je z intervalu (0, 20).
- V první řadě si vložíme nám poskytnuté hodnoty do hustoty funkce v intervalu mezi 0 a 20. Tím zjistíme, že distribuční funkce je 20.
- Dále vložíme do vzorce na obrázku níže naše hodnoty.
- V poslední řadě si zjistíme pravděpodobnost tím, že podle výsledku předchozího vzorce vyhledáme potřebnou pravděpodobnost v tabulkách pro normované normálové rozdělení.
Výsledek je tedy 68,1% pravděpodobnost, že je náhodná veličina A z intervalu (0, 20).
Funkce v Excelu
Při práci s logaritmicko-normálními rozdělení používáme primárně Microsoft Excel. V něm jsou již definované funkce, které můžeme používat. Voláme je pomocí prefixu "=".
LOGNORM.DIST(x,střed_hodn,sm_odchylka,kumulativní)
- x - vybraná hodnota, pro kterou se bude počítat
- střed_hodn - střední hodnota
- sm_odchylka - směrodatná odchylka
- kumulativní
- PRAVDA vrátí kumulativní distribuční funkci
- NEPRAVDA vrátí funkci hustoty pravděpodobnosti
LOGNORM.INV(pravděpodobnost; střed_hodn; sm_odch)
- pravděpodobnost
- střed_hodn - střední hodnota
- sm_odchylka - směrodatná odchylka
Zajímavosti
Jedna ze zajímavosti týkající se logaritmicko-normálního rozdělení lze replikovat následovně:
- Vytvořte sadu dat, která obsahuje náhodná normální čísla s průměrem 100 a směrodatnou odchylkou 5
- Vytvořte nový sloupec čísel s přirozeným logaritmem pro každou náhodnou hodnotu, tedy pro každou náhodnou hodnotu uděláme ln(x)
- Vytvořte logaritmicko-normální pravděpodobnostní graf dat přirozeného logaritmu
- Podívejte se na parametry logaritmicko-normálního rozdělení. Měli by vypadat povědomě
Ano, parametry logaritmicko-normálního rozdělení jsou průměr a směrodatná odchylka normálního rozdělení, které mohly být použity k vytvoření logaritmicko-normálních dat prostřednictvím přirozené logaritmické transformace.[17]
Logaritmicko-normální rozdělení je také možné pozorovat v populárním matematické domněnce, a to Collatzův problém, také známý jako 3n + 1 problém. V tomto případě doplňování různých hodnot za na vytváří grafy velmi blízce připominající logaritmicko-normální rozdělení.
Příklady k procvičení
Logaritmicko-normální rozdělení se velmi podobá normálnímu rozdělení, pro které existuje více podkladů, příkladů i vysvětlení. Je tedy možné si trénovat normální rozdělení, případně lehce upravit zadání pro podobu logaritmického-normálního rozdělení.
Příklad 1
Sběratel známek je dlouholetým zákazníkem pojišťovacího podniku, která pojišťuje jeho sbírku. Tím se dostal mezi vybrané dlouholeté zákazníky, kteří jsou drahocení pro pojišťovnu a mají zvýhodněné pojištění. V rámci tohoto zvýhodnění platí 65 % základního pojistného, které činí 14 900 Kč. Parametr λ Poissonova rozdělení počtu pojistních událostí je roven 0,2 a výše škody se řídí logaritmicko normálním rozdělením s parametry μ=5 a σ2=2:
- určete pravděpodobnost, že klient uplatní pojistnou událost
- určete střední hodnotu škody
Příklad 2
Máme náhodnou veličinu X s logaritmicko-normálním rozdělením s parametry: μ=2; σ2=9.
Určete:
- pravděpodobnost, že náhodná veličina X je z intervalu (0;30)
- medián daného rozdělení
- střední hodnotu a rozptyl náhodné veličiny X
Příklad 3
Předpokládejme, že Y následuje logaritmicko-normální rozdělení s parametry: μ=2; σ2=9. Mějme Y1 = 1,25Y. Zjistěte následujicí:
- Pravděpodobnost, že Y1 bude vyšší než 1.
- 40% kvantil Y1.
- 80% kvantil Y1.
Příklad 4
Předpokládejme, že známe následujicí informace o logaritmicko-normálním rozdělení:
- Spodní kvartil (tedy 25% percentil) je 1000
- Vrchní kvartil (tedy 75% percentil) je 4000
Zjistěte průměr a rozptyl s danými informacemi.
Reference
- ↑ 1.0 1.1 1.2 1.3 1.4 Logaritmicko normální rozdělení. Statistika a pravděpodobnost [online]. [cit. 2022-05-25]. Dostupné z: https://is.muni.cz/do/rect/el/estud/prif/ps15/statistika/web/pages/logaritmicko-normalni.html
- ↑ Lognormal distribution. National institute of Standards and Technology [online]. [cit. 2022-05-25]. Dostupné z: https://www.itl.nist.gov/div898/handbook/eda/section3/eda3669.htm
- ↑ Popisné charakteristiky statistických souborů. Fakulta veterinární hygieny a ekologie Veterinární univerzity Brno - Biostatistika [online]. [cit. 2022-05-25]. Dostupné z: https://cit.vfu.cz/statpotr/POTR/Teorie/Predn1/strednih.htm
- ↑ Popisné charakteristiky statistických souborů. Fakulta veterinární hygieny a ekologie Veterinární univerzity Brno - Biostatistika [online]. [cit. 2022-05-25]. Dostupné z: https://cit.vfu.cz/statpotr/POTR/Teorie/Predn1/variabil.htm
- ↑ Lognormal distribution. Lognormal distribution in base B [online]. [cit. 2022-05-25]. Dostupné z: https://www.vosesoftware.com/riskwiki/images/image1c99.gif
- ↑ OTIPKA, Petr a Vladislav ŠMAJSTRLA. Pravděpodobnost a statistika. Ostrava: Vysoká škola báňská - Technická univerzita Ostrava, 2006. [online]. Dostupné z: https://homel.vsb.cz/~oti73/cdpast1/
- ↑ Log-normal Distribution - A simple explanation [online]. [cit. 2022-05-26]. Dostupné z: https://miro.medium.com/max/1290/1*5yM7k43zgHzE_twI-Y9DXA.png
- ↑ Lognormal distribution [online]. [cit. 2022-05-26]. Dostupné z: http://www.montecarloexceladdin.com/wp-content/uploads/2016/01/LogNormalDistributionCDF.jpg
- ↑ ANTONIOU, I., Vi V. IVANOV, Va V. IVANOV a P.V. ZRELOV. On the log-normal distribution of stock market data [online]. [cit. 2022-05-26]. Dostupné z: https://doi.org/10.1016/j.physa.2003.09.034
- ↑ Mzdová sféra ČR - 1. pololetí 2021. Informační systém o průměru výdělku [online]. [cit. 2022-05-25]. Dostupné z: https://www.ispv.cz/getattachment/eb70c203-d142-4a32-90d6-b48acbb9588b/CR_212_MZS-xlsx.aspx?disposition=attachment
- ↑ 11.0 11.1 Distribution Fitting and Parameterization of Individual Operator Work Routine Times for Small Dairy Parlors [online]. 2006 [cit. 2022-05-25]. Dostupné z: doi:https://doi.org/10.3168/jds.S0022-0302(06)72305-0
- ↑ AHLE, Thomas. What is the average length of a game of chess? [online]. [cit. 2022-05-26]. Dostupné z: https://chess.stackexchange.com/questions/2506/what-is-the-average-length-of-a-game-of-chess/4899#4899
- ↑ Millet, A. A Universal Model for the Log-Normal Distribution of Elasticity in Polymeric Gels and Its Relevance to Mechanical Signature of Biological Tissues. Biology 2021, 10, 64. https://doi.org/10.3390/biology10010064
- ↑ Gros, C., Kaczor, G. & Marković, D. Neuropsychological constraints to human data production on a global scale. Eur. Phys. J. B 85, 28 (2012). https://doi.org/10.1140/epjb/e2011-20581-3
- ↑ Santarelli, E., Klomp, L., Thurik, A.R. (2006). Gibrat’s Law: An Overview of the Empirical Literature. In: Santarelli, E. (eds) Entrepreneurship, Growth, and Innovation. International Studies in Entrepreneurship, vol 12. Springer, Boston, MA. https://doi.org/10.1007/0-387-32314-7_3
- ↑ World Firm Size Distribution and A Test of Gibrat’s Law [online]. [cit. 2022-05-26]. Dostupné z: https://sungyongchang.files.wordpress.com/2014/02/figure1.png?w=480&h=300
- ↑ HAYNES, Rick. An interesting fact about the Lognormal Distribution [online]. [cit. 2022-05-26]. Dostupné z: https://smartersolutions.com/an-interesting-fact-about-the-lognormal-distribution.html/