Schooling of the fish

Problem definition

The aggregate motion of a flock of birds, a herd of land animals, or a school of fish is a beautiful and familiar part of the natural world. A school exhibits many contrasts. It is made up of discrete fish yet overall motion seems fluid. It is simple in concept yet is so visually complex. This simulation proposes that the leaders can emerge as a consequence of a self-organized process based on local rules of dynamic interactions among individuals. Schools are an example of self-organized behaviour in a group where one can study the leadership properties of the individuals. Simulation proposed to monitor and analyze the leadership properties of the school and given individuals. Based on this analysis I tried to identify key factors that influence emergence of the leaders.

Method

The simulated school is an elaboration of an agent based system, with the simulated fish being the agents. The aggregate motion of the simulated school is created by a distributed behavioral model much like that at work in a natural school; the fish choose their own course. Each simulated fish is implemented as an independent agent that navigates according to its local perception of the dynamic environment. The aggregate motion of the simulated school is the result of the dense interaction of the relatively simple behaviors of the individual simulated fish. Fish are bound by certain set of rules explained in later chapters. This simulation is implemented in NetLogo since it provides the best capabilities from available tools. There is a wide range of monitoring tools and visualization approaches in NetLogo which will be used as a part of the simulation.

Model

World and Agents

The agents move in a two-dimensional, discrete world that is unbounded. Time flow in this world is represented by ticks. Each agent (fish) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} is identified by its coordinates and heading at time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle t} . The heading of an agent at time Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle t} is defined as the vector connecting its location at t-1 with its location at t, and is expressed as the clockwise angle between that vector and the Y axis.

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F : \{P, H\}}

where:

• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P_i = \{(x_i(t), y_i(t))\}}
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle H_i = \{\alpha (t)\}}

Fish have a perceptual field which is defined as a circular sector whose centre is the agents current location Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P_i} and which is bisected by its current heading vector. Perceptual field is key model attribute since it defines two important properties of the fish:

• depth of agents perceptual filed - defined by visibility angle Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \alpha_i}
• scope of agents perceptual filed - defined by visibility range (or radius) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle r_i}

both of which can by modified (since they are model attributes).

When the school emerges, fish can be leader, follower or both. Each fish has its rank based on number of followers. Ranking function R is defined as follows:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle R = \tfrac{F}{N - 1}}

where:

• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle F} number of followers
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle N} number of fish

Ranking function yields values from the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle <0; 1>} . Fish can be categorized based on their rank as follows (in big enough population):

• strong leader - rank higher than Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0.3}
• leader - rank from the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (0; 0.3)}
• follower - rank equal to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 0}
• both leader and follower - cannot be determined based solely on ranking function

Leader selection is one of the most critical model attributes. There are two ways fish choose their leader (user can select leader selection strategy since this is also model attribute):

• Distance-based
  • Fish select the closest fish in their perceptual field and this fish becomes the leader
• Rank-based
  • Fish select the fish with highest rank. The closest fish is selected if there are more fish with same rank (the highest ranking visible fish) in question.

Special and also initial case is the situation, when fish do not see any other fish. In this case the fish moves independently of any leaders or other fish.

Controls

User interface is devided into two portions - controls/monitors and animation box. First part is divided as follows:

Simulation controls

Simulation controls are used to initialize, run and stop the simulation.

• setup button - initializes environment and agents and resets all monitors to default values (keyboard shortcut Q)
• run button - runs the simulation (keyboard shortcut W)
• step button - executes one step in the simulation (keyboard shortcut E)

Fish properties

Fish properties define agents basic physical capabilities - they restrict their movement, define their perceptual field and number of agents in the simulation.

• fish-count slider - number of fish in population
• cohorence-of-school slider - minimal distance from leader in the school
• visibility-angle slider - scope of the perceptual field
• visibility-range slider - depth of the perceptual field

Leader selection

Leader selection allows user to select leader selection strategy.

• lss-rank switch
  • ON - rank-based leader selection strategy
  • OFF - distance-based leader selection strategy

Monitors

User is presented with two groups of monitors based on their scope: rank monitors and leader/follower monitors.

• Rank monitors
  • Median of ranks
  • Average of ranks
  • Ranking histogram - displays ranking of the whole population (in given step)
• Leader/Follower monitors
  • Leaders - number of leaders in population (in given step)
  • Followers - number of followers in population (in given step)
  • Fish histogram - complementary histogram displaying Leaders and Followers (in given step)
  • Leaders and followers plot - plots number of leaders and followers since the beginning of the simulation

Model limitations

• Objects do overlap
  • This problem is partially solved for distance-based leader simulation but it quite fails when simulation is switched to rank-based selection strategy.
• Absence of behavior
  • This model is an abstraction of one of the most complex problems in organizational studies and social sciences such as sociology, anthropology or psychology. Due to this fact many properties of the real environment and individuals had to be ignored. (discussed more in later chapters)

Results

The success and validity of these type of simulations is difficult to measure objectively. They do seem to agree well with certain criteria and some statistical properties of natural schools which have been reported by the zoological and behavioral sciences. Perhaps more significantly, many people who view these animated schools immediately recognize them as a representation of a natural school. One can study certain aspects of biology in order to verify certain aspects of this simulation. It is always a good idea to research relevant or similar thesis/paper/simulation when you are trying to provide any relevant information by your simulation. And thats why I would start with formulating some hypotheses based on my research of related works before unveiling any results. After presenting hypotheses enumeration I describe my tests and discuss implication of the results in regard to the postulated hypotheses.

Hypotheses

1. the bigger the world is, the more difficult it is for a school to emerge
2. the smaller the world is, the less stable the school is
3. certain values of agent features could favour school emergence
4. agents spatial position influences their chances of becoming leader
5. one of critical factors of school emergence is perception of an agent
6. in the invariable environment there might be a pattern hidden in the stability of the school
7. there can be only one strong leader in the population
8. rank-based leader selection strategy produces bigger and more stable schools
9. stability of the school is not guaranteed

Results

One of the most important concepts used in this simulation is the emergence of the school. In this series series of tests I focused on an average number of the schools in the environment during the run. I conducted two test suits - one for each leader selection strategy. Each test suit contained characteristic number of the fish (small - 15, medium - 35, large - 50). An average number of schools was calculated in each of three mile stones (early stage - 1 000 ticks, middle stage - 10 000 ticks, late stage - 100 000 ticks). Goal of this test is to explore the relationship between time and school stability.

Average number of schools after certain time period

Based on the table above we might conclude that hypothesis 2 is confirmed. Hypothesis 2 proposes that the smaller the world is, the less stable the school is which is confirmed, since nearly all table rows point to the fact, that the bigger the population is (and thus the world is smaller), the larger the average number of schools become.

Another interesting test that was conducted was aimed at the influence of the world resolution on emergence of the schools. Again two sets of test suits were run - test populations remained unchanged and new test attribute was introduced - resolution of the world (small - 26x26, medium - 50x50, large - 100x100). Goal of this test is to explore the relationship between world resolution and school emergence.

Average number of ticks up to the emergence of the first school

Based on second test we can say that also hypothesis 1 was proven, since all of the data support its claim. Simply put the bigger the world, the longer fish search for each other. Another hypothesis (not mentioned above) could state that time required for a school to emerge is independent of leader selection strategy (at least two strategies presented in this simulation). This claim is also proven by the second table, since there are no significant differences between both strategies.

Influence of the perceptual field

Average number of schools based on variable scope

Average number of schools based on variable radius

Perception of an agent is one of its most critical properties. Following tests put this claim to the test. In this chapter I am going to reason about the role of agents scope and depth of the perception field.

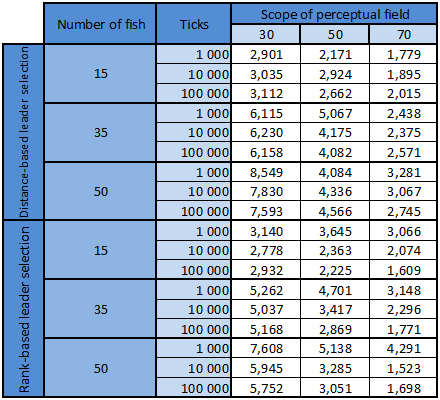
Scope of the perception field

The most important thing to notice is, that data in all the rows (except two fields in row 10) confirm this claim. Therefore I think it's safe to say, that hypotheses 3 and 5 are proofed (since they complement each other). The underlaying logic is quite simple. Wider the range of what agent sees, the better the opportunity of finding suitable leader gets.

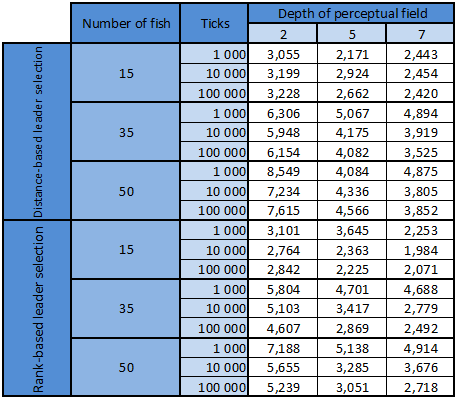
Depth of the perception field

To my surprise this test did not end in such an strong pro claim result. Even thought test proves the claim, I must admit a expected the result to be more like in the scope test. Logic backing this claim is also pretty straight forward: the deeper your perception field is, the better a chance of seeing a leader in a distance is.

Combination of both

Test where both factors are set to minimum or maximum was not conducted in statistical manner but only by observation. Nevertheless one can expect that when both scope and depth are set to their maximum values resulting effect would cause (and vise-versa):

1. easier emergence of schools (they emerge faster)
2. more stable schools
3. schools containing more members over the time

Model and reality

<TODO>

Conclusion

<TODO>

Model source code

<TODO>