Probability distributions/cs
Contents
Úvod
Pravděpodobnost nějakého náhodného jevu nám říká, jakou máme šanci, že daný jev nastane. Při řešení úloh z oblasti pravděpodobnosti nahrazujeme náhodné jevy určitými hodnotami proměnlivé veličiny [1]
Abychom si mohli popsat, co že to vlastně pravděpodobnostní rozdělení je, pojďme se nejdříve podívat na pojem Náhodná veličina.
Náhodná veličina
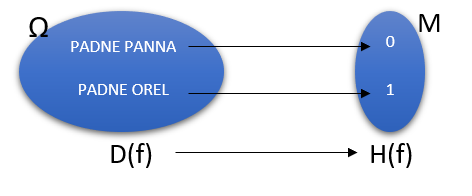
Některé pokusy mají výsledek (elementární jev) vyjádřený přímo číselně – například, že padne číslo 6. U jiných jevů tomu tak být nemusí – například, že na minci padne orel. Nicméně i těmto jevům je výhodné přiřadit čísla.
Čísla přiřazená elementárním jevům tvoří obor hodnot M proměnné, kterou nazýváme náhodná veličina (označujeme X, Y, Z, …).
[2]
Podle oboru hodnot M rozdělujeme náhodné veličiny na:
• Diskrétní -> obor hodnot M je konečná nebo nekonečná posloupnost
• Spojité -> obor hodnot M je otevřený nebo uzavřený interval
Diskrétní a spojité náhodné veličiny

Diskrétní náhodné veličiny: mohou nabývat nanejvýš spočetně mnoha hodnot. Výsledkem jednoho náhodného pokusu je to, že náhodná veličina bude mít právě jednu hodnotu.
[4]
Příklady:
• Počet šestek při deseti hodech kostkou
• Na kolikátý pokus se podaří vyvolat studenta, který něco umí
• Počet procent vadných součástek v balíku s 25-ti kusy
Spojité náhodné veličiny: (zjednodušeně) mohou nabývat všech hodnot z určitého intervalu. Rozdělení spojité náhodné veličiny nelze popsat pravděpodobnostní funkcí v určitém bodě.
[4]
Příklady:
• Naměřená hodnota napětí
• Délka časového intervalu mezi dvěma událostmi
Pravděpodobnostní rozdělení
Vraťme se nyní k pravděpodobnostnímu rozdělení.
Pravděpodobnostní rozdělení nebo rozdělení pravděpodobnosti náhodné veličiny je pravidlo, díky kterému se každému jevu, který tato veličina popisuje, přiřazuje určitá pravděpodobnost.
Pravděpodobnostní rozdělené můžeme chápat také jako zobrazení, které každému elementárnímu jevu přiřazuje určité reálné číslo – takové číslo charakterizuje pravděpodobnost tohoto jevu.
Rozdělení pravděpodobnosti náhodné veličiny vznikne, pokud je každé hodnotě diskrétní náhodné veličiny nebo intervalu hodnot spojité náhodné veličiny přiřazena pravděpodobnost.[5]
Základní pojmy
K pochopení pravděpodobnosti a jejího rozdělení je nutné znát základní pojmy, které si nyní představíme:
Distribuční funkce

Jedním z prostředků pro popis náhodné veličiny (spojité i diskrétní) je distribuční funkce. Tato funkce každému reálnému číslu přiřazuje pravděpodobnost, že náhodná veličina nabude hodnoty menší nebo rovné než toto číslo.
[7]
Distribuční funkce náhodné veličiny X:
Vlastnosti distribuční funkce:
[8]
• Hodnoty distribuční funkce leží mezi 0 a 1
• Distribuční funkce je funkcí neklesající, pro všechna x2>x1 tedy platí:
• Pro každou distribuční funkci je:
• Je zprava spojitá
• Má nejvýše spočetně mnoho bodů nespojitosti
• Distribuční funkce náhodné veličiny spojitého typu je spojitá a distribuční funkce náhodné veličiny diskrétního typu je nespojitá.
Pravděpodobnostní funkce

Pro popis diskrétní (nespojité) náhodné veličiny se používá pravděpodobnostní funkce.
Definice: Pravděpodobnostní funkce p(x) náhodné veličiny X přiřazuje každému reálnému číslu c pravděpodobnost, že náhodná veličina nabude této hodnoty tedy:
[9]
Pravděpodobnostní funkci p(x) můžeme vyjádřit grafem (obrázek napravo), tabulkou,
nebo matematickým vzorcem.

Hustota pravděpodobnosti

U spojité náhodné veličiny se místo pravděpodobnostní funkce používá funkce hustoty pravděpodobnosti.
Definice: Funkce hustoty pravděpodobnosti spojité náhodné veličiny X je nezáporná funkce f(x) taková, že
[11]
Na následujícím obrázku můžeme vidět hustotu pravděpodobnosti několika normálních rozdělení.
![Hustota pravděpodobnosti několika normálních rozdělení.[5].](/images/Herm10_obr4.PNG)
Střední hodnota

Střední hodnota (aritmetický průměr) je definován jako součet všech hodnot náhodné proměnné Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_i}
dělený počtem hodnot. Vypočtený průměr pak udává, jaká stejná část z úhrnu hodnot sledované číselné proměnné připadá na jednu jednotku souboru (jednoho jedince).
[12]
Střední hodnota náhodné veličiny X, kde Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle g: R \to R}
je (měřitelná) funkce, je:
• pro X diskrétně rozdělenou s pravděpodobnostní funkcí P definována jako
• pro X spojitě rozdělenou s hustotou f jako
mají-li výrazy na pravé straně rovnice smysl.
Rozptyl
Rozptyl nám udává, jak moc jsou hodnoty v našem statistickém soubory rozptýleny. Rozptylu se někdy říká také variance - je to ukazatel variability (měnivosti). Řečeno definicí:
Rozptyl Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma^2}
je průměrem druhých mocnin odchylek jednotlivých hodnot od aritmetického průměru z hodnot statistického souboru.
[13]
[14]
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma^2}
... rozptyl
n ..... počet prvků statistického souboru
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x_i}
... prvek statistického souboru o indexu i
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \overline{x}}
..... prostý aritmetický průměr
Kvantily

Kvantily rozdělují množinu náhodných proměnných na určité části. Dělí prostor náhodných proměnných na část jevů, které nastanou s pravděpodobností menší nebo rovnou kvantilu a druhá část jevů s pravděpodobností rovnou 1 - kvantil. Medián je například kvantil o hodnotě 0.5. Dělí tedy prostor náhodných proměnných na dvě stejně pravděpodobné části.
Specifické názvy kvantilů:
• kvartily: 0.25, 0.5, 0.75
• decily: 0.1, 0.2, 0.9
• centily: 0.01, 0.02, 0.99
Typy rozdělení
Jak již vyplývá z výše uvedených pojmů, typy rozdělení se nám v první řadě dělí na rozdělení pravděpodobnosti diskrétní a spojité náhodné veličiny. Dále pak existují například vícerozměrná rozdělení pravděpodobnosti, kterými se ale tento učební text nezabývá.
Nyní se pojďme podívat na důležitá pravděpodobnostní rozdělení, z nichž si většinu zde představíme podrobněji.
Důležitá diskrétní rozdělení
[5]
• Alternativní rozdělení (X nabývá pouze dvou hodnot 0 nebo 1)
• Binomické rozdělení (n pokusů se stejnou pravděpodobností)
• Poissonovo rozdělení
• Negativně binomické rozdělení
• Pascalovo rozdělení (speciální případ negativně binomického rozdělení)
• Geometrické rozdělení (speciální případ Pascalova rozdělení)
• Hypergeometrické rozdělení
• Logaritmické rozdělení
Důležitá spojitá rozdělení
[5]
• Rovnoměrné rozdělení
• Normální rozdělení (označované také jako Gaussovo rozdělení)
• Logaritmicko-normální rozdělení (také log-normální rozdělení)
• Exponenciální rozdělení
• Cauchyho rozdělení
• Gama rozdělení
• Laplaceovo rozdělení (nebo také dvojitě exponenciální rozdělení)
• Logistické rozdělení
• Maxwellovo-Boltzmannovo rozdělení
• Studentovo rozdělení
• Fisherovo-Snedecorovo rozdělení
• χ² rozdělení (Chí kvadrát)
Základní typy rozdělení pravděpodobnosti diskrétní náhodné veličiny
Alternativní rozdělení
Používá se, když má náhodný pokus pouze dva možné výsledky => úspěch; neúspěch.
[15][16]

Příklad:
[17]
Házíme jedenkrát kostkou. Najděte pravděpodobnostní funkci náhodné veličiny X, která udává, jestli v daném hodu padlo číslo menší než 3.
Řešení:
Obor hodnot obsahuje dva prvky: M= {0,1}. Úspěch v našem případě znamená, že padlo číslo menší než 3, a to číslo 1 nebo 2. Neúspěch značí, že padla čísla 3, 4, 5 nebo 6.
Tedy:
Pravděpodobnostní funkce náhodné veličiny X je tvaru:

Binomické rozdělení

Náhodná veličina udává počet úspěchů v posloupnosti n nezávislých alternativních pokusů. Binomické rozdělení vychází z Bernoulliova pokusu, který spočívá v tom, že v daném náhodném pokusu mohou nastat pouze dva stavy: úspěch, neúspěch.[15][16]

Příklad:[17]
Zásilka obsahuje 85 % kvalitních a 15 % nekvalitních výrobků. Náhodně s vracením vybereme 4 výrobky. Určete pravděpodobnost, že právě 3 z nich budou kvalitní.
Řešení:
Náhodná veličina X udává počet vybraných kvalitních výrobků,X∼Bi(4;0,85).
Pravděpodobnost, že právě 3 výrobky z námi vybraných 4 budou kvalitní, je 36,85 %.
Negativně binomické rozdělení
Rozdělení počtu neúspěchů předcházejících n-tému úspěchu v posloupnosti nezávislých pokusů. Ekvivalentem k NB(1, p) je Geo(p).[15][16]

Geometrické rozdělení

Udává počet neúspěchů před prvním úspěchem v posloupnosti nezávislých pokusů.[15][16]

Příklad:[17]
Ve firmě je známé, že na výběrové řízení na určitou pozici se dostaví uchazeč s vysokoškolským vzděláním s pravděpodobností 0,65, a uchazeč bez vysokoškolského vzdělání s pravděpodobností 0,35. Určete pravděpodobnost, že až čtvrtý uchazeč o danou pozici bude mít vysokoškolské vzdělání.
Řešení:
Náhodná veličina X∼Ge(0,65).
Pravděpodobnost, že o pozici ve firmě se až jako čtvrtý bude ucházet člověk s vysokoškolským vzděláním, je 2,79 %.
Poissonovo rozdělení

Náhodná veličina X charakterizuje počet výskytů události, která nastane za časovou jednotku. Například jaká je pravděpodobnost, že v následujících dvaceti minutách přijde do obchodu pět lidí.
K událostem dochází náhodně, jednotlivě a vzájemně nezávisle. Průměrný počet událostí za časovou jednotku je roven parametru λ.[15][16]

Příklad:[17]
Předpokládejme, že realitní makléř jedná v průměru s 5 zákazníky za den. Jaká je pravděpodobnost, že počet zákazníků makléře za jeden den bude právě 5.
Řešení:
Náhodná veličina X udává počet zákazníků makléře za den,X∼Po(5).
S pravděpodobností 17,55 % bude mít v průběhu dne makléř právě 5 zákazníků.
Hypergeometrické rozdělení
Máme N prvků, mezi kterými je M prvků se sledovanou vlastností. Pokus opakujeme n-krát. Jednotlivé pokusy jsou vzájemně závislé => výsledek v jakémkoli pokusu závisí na předešlých pokusech. Je to tedy výběr bez vracení.[15][16]
Příklad:[17]
V bance mají seznam 50 žadatelů o úvěr. Mezi nimi je 35 spolehlivých a 15 nespolehlivých žadatelů. Určete pravděpodobnost, že jestli banka poskytne úvěr právě 20 žadatelům, bude z nich 15 spolehlivých a 5 nespolehlivých.
Řešení:
• N = 150 .... všichni žadatelé
• M = 35 ..... spolehliví žadatelé
• N-M = 15 ... nespolehliví žadatelé
• n = 20 ..... počet poskytnutých úvěrů
• x = 15 ..... vybraní spolehliví zájemci
• n-x = 5 .... vybraní nespolehliví zájemci
Pak námi hledaná pravděpodobnost je:
Pravděpodobnost, že z 20-ti poskytnutých úvěrů bude 15 poskytnutých spolehlivým žadatelům a 5 nespolehlivým žadatelům, je 20,7 %.
Základní typy rozdělení pravděpodobnosti spojité náhodné veličiny
Rovnoměrné rozdělení

Rozdělení s konstantní hustotou, tedy každá hodnota z intervalu (a, b) je stejně pravděpodobná.[15][16]

Příklad:[17]
Na prezentaci nově založené firmy je každých 20 minut promítána krátká prezentace o jejich vymezených cílech. Určete pravděpodobnost, že jestli náhodně přijdeme do promítací místnosti, nebudeme čekat více jak 5 minut.
Řešení:
Náhodná veličina X udává dobu čekání na prezentaci, X∼R(0,20).
Normální rozdělení (Gausovo)

Nejdůležitější rozdělení spojitého typu, jelikož[15][16]:
• vyskytuje se nejčastěji
• blíží se mu mnoho jiných rozdělení
• řada jiných rozdělení se jím dá nahradit

Příklad:[17]
Jistá firma se rozhodla podrobit své zaměstnance IQ testu. Průměrná hodnota IQ testu byla 115, směrodatná odchylka 16. Předpokládejme, že hodnoty IQ testu se řídí normálním rozdělením. Určete pravděpodobnost, že hodnota IQ testu při náhodně vybraném zaměstnanci nabude hodnoty menší nebo rovné než 120.
Řešení:
Náhodná veličina X udává hodnotu IQ testu, X∼N(115,162).
Hodnota IQ testu nabude hodnoty menší nebo rovné jak 120 s pravděpodobností 61,17 %.
Normované normální rozdělení
Jedná se o speciální případ obecného normálního rozložení, kdy µ = 0, σ^2 = 1.[15][16]

Exponenciální rozdělení

Představuje dobu čekání do nastoupení (poissonovského) náhodného jevu, nebo délku intervalu (časového nebo délkového) mezi takovými dvěma jevy (např. doba čekání na obsluhu, vzdálenost mezi dvěma poškozenými místy na silnici).
Závisí na parametru λ, což je převrácená hodnota střední hodnoty doby čekání do nastoupení sledovaného jevu.[15][16]

Příklad:[17]
Životnost určitého výrobku se řídí exponenciálním rozdělením se střední hodnotou životnosti 200 hodin. Určete pravděpodobnost, že daný výrobek bude funkční nejvýše 150 hodin.
Řešení:
Víme, že: E(X)=200 hodin, tedy X∼Ex(1200),λ=0,005.
S pravděpodobností 52,76 % bude výrobek funkční nejvýše 150 hodin.
Logaritmicko-normální rozdělení
Náhodná veličina X má logaritmicko-normální rozdělení s parametry μ, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma^2(X)}
, jestliže ln(X) má normální rozdělení N(μ,σ^2)[15][16]

Příklad:[17]
Nechť X je náhodná veličina s logaritmicko normálním rozdělením s parametry μ=2 a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sigma^2(X)}
=9. Určete pravděpodobnost, že náhodná veličina X je z intervalu (0,30).
Řešení:
Náhodná veličina X∼LN(2;9), hledaná pravděpodobnost je:
Cauchyho rozdělení
Hustota je symetrická kolem a, momenty neexistují, E |X| = +∞.[15][16]

Gama rozdělení
Gama rozdělení se obvykle používá při analýze front.[15][16]

Citace
- ↑ KŘÍŽ, Oldřich, Jiří NEUBAUER a Marek SEDLAČÍK. Pravděpodobnost a náhodná veličina: učební text pro distanční studium. Brno: Univerzita obrany, vydáno 2008, 43s. ISBN 978-80-7231-488-1
- ↑ OTIPKA, Petr a Vladislav ŠMAJSTRLA. Pravděpodobnost a statistika., Ostrava: Vysoká škola báňská - Technická univerzita, 2006. 72s ISBN 80-248-1194-4.
- ↑ Náhodná veličina [online]. [cit. 2020-05-26]. Dostupné z: http://books.fs.vsb.cz/SystAnal/texty/07.htm
- ↑ 4.0 4.1 Fakulta elektrotechniky a komunikačních technologií VUT v Brně Náhodná veličina [online]. [cit. 2020-05-15] Dostupné z: http://www.umat.feec.vutbr.cz/~hlavicka/vyuka/BMA3_predn/prednaska02.pdf
- ↑ 5.0 5.1 5.2 5.3 5.4 Rozdělení pravděpodobnosti [online]. [cit. 2020-05-25]. Dostupné z: https://www.wikiwand.com/cs/Rozd%C4%9Blen%C3%AD_pravd%C4%9Bpodobnosti
- ↑ Distribuční funkce [online]. [cit. 2020-05-26]. Dostupné z: https://cit.vfu.cz/statpotr/POTR/Teorie/Predn1/distrib.htm
- ↑ MAREK, Patrice Náhodná veličina a její popis [online]. [cit. 2020-05-15] Dostupné z: http://physics.ujep.cz/~mmaly/vyuka/poc_fyz_1/NahodnaVelicina_zaklady.pdf
- ↑ Distribuční funkce [online]. [cit. 2020-05-15] Dostupné z: https://iastat.vse.cz/Dfunkce.htm
- ↑ KŘÍŽ, Oldřich, Jiří NEUBAUER a Marek SEDLAČÍK. Pravděpodobnost a náhodná veličina: učební text pro distanční studium. Brno: Univerzita obrany, vydáno 2008, 46s. ISBN 978-80-7231-488-1
- ↑ 10.0 10.1 10.2 10.3 10.4 10.5 10.6 10.7 Pravděpodobnostní rozdělení [online]. [cit. 2020-05-28]. Dostupné z: https://docplayer.cz/1838424-Rovnomerne-rozdeleni.html
- ↑ KŘÍŽ, Oldřich, Jiří NEUBAUER a Marek SEDLAČÍK. Pravděpodobnost a náhodná veličina: učební text pro distanční studium. Brno: Univerzita obrany, vydáno 2008, 50s. ISBN 978-80-7231-488-1
- ↑ FRIESL, Michal Střední hodnota [online]. 2014-02-08 [cit. 2020-05-10] Dostupné z: http://home.zcu.cz/~friesl/hpsb/e.html
- ↑ Rozptyl [online]. © 2006—2014 [cit. 2020-05-10] Dostupné z: https://matematika.cz/rozptyl
- ↑ VACHTOVÁ, Jitka Rozptyl [online]. 2020 [cit. 2020-05-10] Dostupné z: https://www.ekovyp.cz/rozptyl
- ↑ 15.00 15.01 15.02 15.03 15.04 15.05 15.06 15.07 15.08 15.09 15.10 15.11 15.12 KULICH, Michal Přehled pravděpodobnostních rozdělení Matematicko-fyzikální fakulta Univerzita Karlova 2009 [online]. [cit. 2020-05-10]. Dostupné z: http://www.karlin.mff.cuni.cz/~pesta/NSTP097/rozdeleni.pdf
- ↑ 16.00 16.01 16.02 16.03 16.04 16.05 16.06 16.07 16.08 16.09 16.10 16.11 16.12 OTIPKA, Petr a Vladislav ŠMAJSTRLA. Pravděpodobnost a statistika., Ostrava: Vysoká škola báňská - Technická univerzita, 2006. ISBN 80-248-1194-4.
- ↑ 17.0 17.1 17.2 17.3 17.4 17.5 17.6 17.7 17.8 BUDÍKOVÁ, Marie a ŠÁLYOVÁ, Jitka Vybraná pravděpodobnostní rozložení Přírodovědecká fakulta Masarykovy University [online]. [cit. 2020-05-10]. Dostupné z: https://is.muni.cz/do/rect/el/estud/prif/ps15/statistika/web/index2.html
- ↑ Binomické rozdělení [online]. [cit. 2020-05-28]. Dostupné z: https://portal.matematickabiologie.cz/index.php?pg=aplikovana-analyza-klinickych-a-biologickych-dat--biostatistika-pro-matematickou-biologii--nahodna-velicina-rozdeleni-pravdepodobnosti-a-realna-data--dalsi-rozdeleni-pravdepodobnosti--binomicke-rozdeleni