Optimalizace výměn a seřízení sekacích nožů při výrobě dřevařské štěpky

Úvodem

Vítejte na stránkách semestrální práce z předmětu 4IT495 - Simulace systémů. Tato práce se zaměřuje na simulaci a vyhodnocení optimálního intervalu pro výměnu sekacích nožů v rotační sekačce v papírenském závodu Mondi Štětí a.s. Při řešení této otázky byla použita simulace Monte Carlo s využitím nástroje Excel 2016. Jako podklady pro simulaci byly využity reálné hodnoty vyplívající ze současné výroby.

Zadání

Název simulace: Optimalizace výměn a seřízení sekacích nožů při výrobě dřevařské štěpky

Předmět: 4IT495 Simulace systémů (LS 2015/2016)

Autor: Bc. Jakub Kos

Typ modelu: Monte Carlo

Modelovací nástroj: Excel

Představení společnosti

Společnost Mondi Štětí a.s. je předním světovým výrobcem papírových materiálů, papíru a buničiny. Díky významným investicím do zvýšení kapacit a zlepšení jakosti výrobků Mondi Štětí a.s. je nyní největším výrobcem papírových obalů a buničiny na českém trhu. Společnost Mondi Štětí a.s. sídlí v severních Čechách ve Štětí. Areál závodu představuje přibližně polovinu rozlohy města. Tato simulace se omezuje na provoz Zpracování dřeva, kde dochází k výrobě dřevařské štěpky.

Definice problému

Jedním z hlavních klíčových indikátorů výroby úseku Zpracování dřeva je procentuální zastoupení vyrobené optimální štěpky. Štěpka vzniká nasekáním odkorněného dřeva v rotační sekačce s osazenými sekacími noži. S průběhem výroby dochází k opotřebení sekacích nožů a tím se ovlivňuje kvalita štěpky. Seká se více nežádoucích frakcí a méně žádoucích. Poměr frakcí hraje roli při dalším technologickém zpracování při výrobě papíru, proto je potřeba dodržet optimální velikost štěpky. Procento optimální štěpky tedy součet frakcí 3., 4. a 5. je třeba držet co nejvíce nad 80%.

Cíl simulace

• Zjistit optimální interval výměny nožů.

Popis štěpky

Štěpka je meziprodukt při výrobě papíru. Jedná se o na kousky nasekané odkorněné dřevo. V navazujících provozech a technologických postupech dochází k rozvaření štěpky na buničinu, která se následně nalevá na síta a sušením vzniká papír.

Frakce štěpky

V každém zkoumaném množství štěpky se pozorují dané charakteristiky, dle kterých se určuje kvalita štěpky. Jedná se o distribuci velikosti jednotlivých kusů a o vlhkost (vlhkost není tématem této práce). Při tloušťkové analýze se pomocí nástroje Lorenz-Wettre oddělí jednotlivé frakce, které se následně váží a zjištuje se jejich procentuální zastoupení.

1. frakce (F1)

První frakce představuje největší kusy štěpky ve vybraném vzorku.

• Tloušťka 45mm a větší.

2. frakce (F2)

Druhá frakce představuje vetšinou dlouhé vlasovité kusy štěpky ve vybraném vzorku.

• Tloušťka 8mm a větší.

3. frakce (F3)

Třetí frakce představuje větší přijatelné kusy štěpky ve vybraném vzorku.

• Tloušťka 13mm a větší.

4. frakce (F4)

Čtvrtá frakce představuje menší přijatelné kusy štěpky ve vybraném vzorku.

• Tloušťka 7mm a větší.

5. frakce (F5)

Pátá frakce představuje takzvané "sirky".Tvar a velikost kusů odpovídá klasické zápalce.

• Tloušťka 3mm a větší.

6. frakce (F6)

Šestá frakce představuje nejmenší součásti vzorku. Jendá se o piliny a prach.

Požadavek na kvalitu štěpky

• součet procentuálního zastoupení 3., 4. a 5. frakce ve vybraném vzorku nad 80%.

Metoda

Pro řešení tohoto problému jsem si zvolil metodu Monte Carlo, a to v programu Microsoft Excel 2016. Metoda je pro toto zadání vhodná kvůli využití velkého množství generovaných pseudonáhodných čísel. V tomto modelu bylo generováno 30000 řádků jendotlivých "vzorků štěpky".

Nástroj Microsoft Excel 2016 jsem si vybral z důvodu seznámí se s funkcemi v průběhu výuky. Nenarazil jsem v průběhu simulace na žádná omezení ze strany nástroje.

Model

Obsah modelu

Listy souboru Simulace-stepka.xlsx:

• Popis - Úvodní list modelu. Obsahuje základní charakteristiky modelu, štěpky a vybraných parametrů. Dále stanovuje otázku, jaký interval výměň nastavit?
• Simulace - List s vlastní logikou simulace. Nastavují se zde výchozí parametry a generuje se zde 30000 pseudonáhodných vzorků.
• FixRunSimulace - Obsahuje jednu z vygenerovaných sestav dat. Z této sestavy je následně odvozen výsledek a závěr.
• Výsledek + grafy - obsahuje závěr simulace, graf simulace a odpověd na otázku z prvního listu.

Metoda vlastní simulace

Definování výchozího vzorku

Výchozí vzorek, tedy střední hodnoty hmotností a směrodatné odchylky pro jednotlivých frakcí v testovácím vzorku, byl vytvořen jako průměrné hodnoty a směrodatné odchylky ze souboru 20 reálně zanalyzovaných vzorků.

Soubor s výchozími 20 vzorky: File:Vychozi vzorky.xlsx

Definování parametrů

Klíčové pro opotřebovávání sekacích nožů je množství posekaného dřeva. To a další parametry je v modelu definováno pomocí vychézích parametrů.

• parametr "počet polen INFEED" je vypočten dle následujícího vzorce. =ZAOKROUHLIT(NÁHČÍSLO()*2+1;1)*$M$2, kde $M$2 znač rychlost dopravníku. Náhodná veličina zde představuje výstup z odkorňovacího bubnu, který není rovnoměrný.

Definování opotřebení nožů v čase

Zatímco paramtery výše jsou údaje z reálných hodnot, tak u opotřebení bylo nutné provést odhad. Výchozí opotřebení bylo stanoveno jako pokles 1% efektivity za každých 1000 posekaných kusů dřeva. Tento odhad byl ověřen u vedoucího údržby provozu. Opotřebení je nadále rovnoměrně rozděleno mezi nastavený počet nožů.

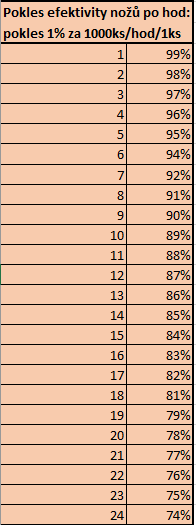Hodnoty pro jednotlivé hodiny jsou vypočteny vzorcem: =(100-$A8*($M$4/1000)/$M$1)/100, kde: $A8 = uběhlá hodina; $M$4 = počet posekaných kusů za hodinu (z paramterů výše); $M$1 = počet nožů.

Generování hodnot testovaných vzorků

Při generování jednotlivých testovacích vzorků byly využity hodnoty z výchozího vzorku. Bylo vygenerováno 30000 řádků.

Vzorec pro výpočet hodnot (1.frakce): =MAX(0;NORM.INV(NÁHČÍSLO();$B$3*$E$8;$B$4)), kde $B$3 = střední hodnota; $E$8 = korekce střední hodnoty; $B$4 = směrodatná odchylka. Funkce MAX byla zabraňuje generování záporných čísel, které jsou v tomto problému nemožné.

Následně je na součet vybraných frakcí aplikována korekce v čase. Z těcho údajů pak odvozuji optimální interval výměny. Pokles je možno vidět i zde. Obrázek zachycuje pouze prvních 18 hod.

Vzorec pro výpočet: =$O36*$B$8, kde $O36 = procentuální zastoupení optimálních frakcí ve vzorku; $B$8 = korekce efektivity z tabulky poklesu výše.

Průběh simulace

Z uložené sestavy vygenerovaných hodnot byl následně zprůměrováním určen trend poklesu optimální štěpky v čase. Vizualizace v podobě grafu se nachází v sekci Výsledek Výsledek