Extensive form/cs

Úvod

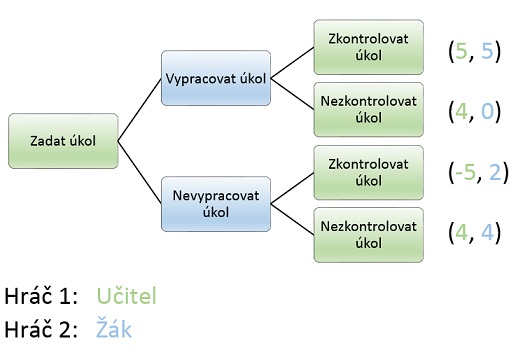
Klasická matice hry v normálním tvaru je vhodná pro grafické znázornění situací, kdy se hráči rozhodují ve stejný okamžik. V případě, kdy se hráči střídají v rozhodování, taková reprezentace již není dostačující, proto se používá tzv. rozšířená forma, která tyto situace zobrazuje pomocí rozhodovacího stromu.

Obrázek výše představuje jednoduchou "hru", kdy se žák rozhoduje, zda vypracovat či nevypracovat domácí úlohu zadanou učitelem. Užitky (vpravo v závorkách) se uvádějí vždy za posledním rozhodovacím krokem. Rozhodovací krok představuje každý uzel v grafu.

Akce vs. strategie

Akcí je právě jedno rozhodnutí. U statických her se rozhoduje zda je výhodnější provést to, či ono, což je samo o sobě výsledkem. Dynamické hry obsahují více uzlů, tedy více akcí ke kterým je nutné učinit rozhodnutí, a to ještě před zahájením samotné hry. Hovoříme tedy o strategii. Strategie je plán akcí pro veškeré situace, které mohou nastat.

Metody řešení

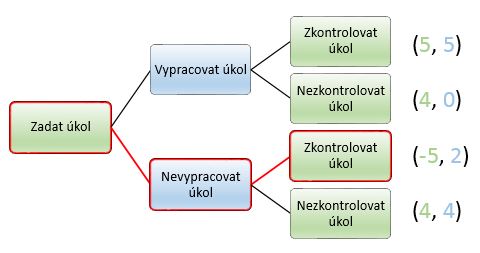
Nejčastěji se používá stejná metoda nejlepších reakcí jako v případě statických her s tím rozdílem, že se neporovnávají akce, nýbž strategie. Strategii lze vyjádřit zvýrazněním cesty od kořene grafu až k jednomu z jeho posledních potomků.

V předešlém případě značíme červeně vyznačenou strategii takto: <Zadat úkol, Zkontrolovat úkol>; <Nevypracovat úkol> nebo zkráceně: <Z, Z>; <N>. Tato strategie však není kompletní, protože v ní nejsou zahrnuty veškeré situace, které mohou nastat, tj. pokud se žák rozhodne vypracovat úkol, učitel nebude mít pro tuto možnost stanovenou strategii. Pojďme si tedy ukázat, jak postupovat správně při hledání optimálního řešení dynamických her.

Zpětná indukce

Předchozí příklad je příkladem hry s nekompletní informací, tj. v situaci, kdy se učitel rozhoduje zda úkol zkontrolovat, či nikoliv, tak nemá informaci o tom, zda žák úkol vypracoval nebo ne. K tomuto typu příkladů se ještě vrátíme, ale pro začátek si vysvětlíme metodu zpětné indukce na příkladu tzv. Escalation game.

Dva státy se dostanou do sporu o území.