Pension System Czech Republic
Contents
Introduction
Simulation of pension reform in the Czech Republic: Analysis of long-term sustainability
What will be simulated:
A system dynamics model of the Czech pension system that simulates the long-term financial sustainability under varying demographic, economic, and policy scenarios. The simulation will project future balances of the pension system, incorporating the flows of revenues (social insurance contributions) and expenditures (pension payouts)
Problem definition
The main goal is to analyze how different pension reform strategies (e.g., adjusting retirement age, altering contribution rates, changing the indexation formula of pensions) will affect the long-term stability of the Czech pension system. The simulation aims to identify specific policy levers and thresholds that ensure the pension system’s financial equilibrium over a multi-decade horizon, despite changing demographic and economic conditions.
Method
The System Dynamics method was chosen for its ability to model complex systems with multiple influencing variables, inflows, and outflows. Alternative approaches, such as Monte Carlo analysis or agent-based modeling in NetLogo, were deemed unsuitable for this case as they cannot adequately capture the dynamic interactions and feedback loops between demographic, economic, and policy variables. Vensim PLE was selected as the simulation environment due to its accessibility and support for this type of modeling.
Model
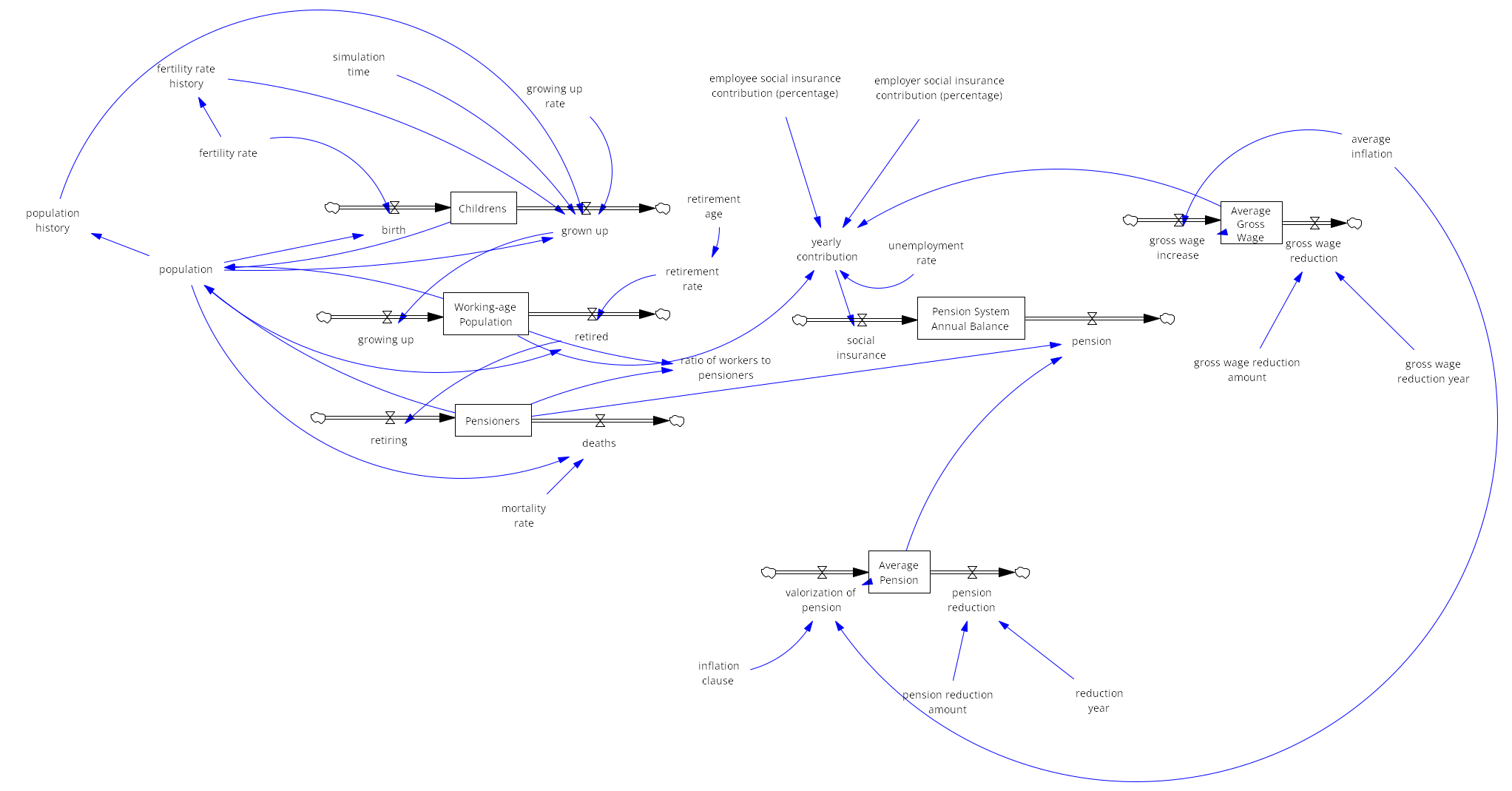
The model represents the dynamics of the Czech pension system, divided into key components: population structure, contributions to the pension system, and pension expenditures.
Population structure
The population is categorized into children (ages 0–19), working-age population (ages 20–64), and pensioners (65+ years). Children grow up and transition into the working-age population, which contributes to the pension system through employment. Over time, individuals retire and become pensioners, withdrawing from the pension system. The retirement age determines the rate at which the working-age population transitions to retirement, with a higher retirement age reducing the retirement rate and vice versa.
Contribution to the pension system
The working-age population contributes to the system through social insurance contributions, based on the average gross wage. Contributions come from both employees and employers, while unemployment reduces the total contributions collected. The model assumes that the gross wage grows annually, at least partially indexed to inflation (e.g., one-third of the inflation rate).
Pension expenditures
Pensioners withdraw funds from the system based on the average pension, which is periodically adjusted through pension valorization. The inflation clause determines the extent to which pensions are indexed to inflation, ensuring their real value remains stable over time.
External adjustments
The model includes variables for one time reductions in both the average gross wage and the average pension in a specific year. These adjustments simulate policy interventions (e.g., government mandated pension reductions) or external shocks (e.g., an economic crisis) that impact wages or pensions.
This dynamic interaction between population groups, contribution flows, and pension expenditures allows for the simulation of various policy scenarios, illustrating the long-term sustainability of the pension system.
Variables
Population variables
- Childrens: Represents the population aged 0-19 and serves as new entrants to the future workforce.
- birth: Represents the number of children entering the stock of "Children" annually, driven by the fertility rate.
- grown up: Represents the transition of individuals from "Children" to "Working-age Population," determined by the growing up rate (later the figure reflects the number of births before 20 years).
- Working-age Population: Population aged 20-64, representing workers contributing to the pension system.
- growing up: Transition from "Children" stock into "Working-age Population."
- retired: Represents the number of individuals leaving the working-age population to become pensioners, driven by the retirement rate.
- Pensioners: Population aged 65 and above, representing beneficiaries of the pension system.
- retiring: Transition of individuals from "Working-age Population" to "Pensioners."
- deaths: Represents the number of pensioners leaving the stock due to mortality, driven by the mortality rate.
Policy variables
- retirement age: Defines the age at which individuals become eligible for a pension. Higher retirement age reduces the retirement rate, delaying transitions into the pensioner stock and vice versa.
- employee social insurance contribution (percentage): The percentage of an employee’s wage contributed to the pension system
- employer social insurance contribution (percentage): This is the percentage paid by the employer on behalf of their employee into the pension system.
- inflation clause: A mechanism that adjusts pensions annually based on inflation, specifying not just whether adjustments occur, but also to what extent (e.g., full inflation, partial indexing like 50%, or less).
Economic variables
- Average Gross Wage: Represents the average income of workers, directly impacting total contributions to the pension system.
- gross wage increase: Represents annual growth in average wages due to economic factors like inflation.
- gross wage reduction: Represents potential reductions in wages caused by economic crises or policy changes.
- Average Pension: It represents the average pension paid to pensioners.
- valorization of pension: Reflects annual adjustments to pensions, linked to inflation and indexation mechanisms (valorization).
- pension reduction: One time reduction in the average pension amount, simulating government mandated adjustments.
Fiscal variables
- Pension System Annual Balance: Tracks the annual difference between contributions collected and pensions paid, indicating the system's financial health.
- social insurance: Total contributions collected driven by yearly contribution.
- pension: Total annual expenditure on pensions, calculated as the product of the number of pensioners and the average pension.
- yearly contribution: Total revenue collected from working-age population contributions, influenced by unemployment rate, average gross wage, and contribution percentages.
- unemployment rate: The proportion of the working-age population that is unemployed, reducing total contributions.
Random variables
- fertility rate: Reflects the probabilistic distribution based on historical data and birth predictions, providing insights into future workforce size and population growth..
- mortality rate: Mortality rate reflects the probabilistic distribution based on historical data and mortality predictions, providing insights into life expectancy and death rates, which influence population transitions and pension payouts.
- average inflation: Reflects a probabilistic function derived from the median of historical inflation data, capturing economic variability through stochastic projections.
- retirement rate: It corresponds to the variability in the number of people retiring each year.
- growing up rate: Simulates the transition of children (aged 0-19) into the working-age population, based on fertility patterns for the first 20 years and precise simulation data thereafter.
Auxiliary variables
- fertility rate history: Stores historical fertility rates to project future workforce accurately after 20 years.
- population history: Tracks past population levels for precise calculations in future aging.
- simulation time: Tracks the current simulation cycle for transitioning between estimated and precise aging.
- population: Represents the total population at any simulation step, serving as the sum of all age groups.
Economic adjustment variables
- gross wage reduction amount: Simulates reductions in the average wage due to policy or economic crises.
- gross wage reduction year: Specifies the year when a reduction in average wages occurs.
- pension reduction amount: Simulates government measures to reduce pensions, implemented as part of necessary fiscal adjustments.
- reduction year: Identifies the year when a pension reduction is implemented.
'Variables for measurable metrics
- ratio of workers to pensioners: A key metric representing the dependency ratio, calculated as the number of working-age individuals per pensioner.
Variables Data
Population variables
- Childrens (Number of children at start (2021 - census)):
- children age = 0 – 19
- number of children = 2,181,596
- Working-age Population (Number of working-age population at start (2021 - census)):
- working-age population = 20 – 64
- number of working-age = 6,194,523
- Pensioners (Number of pensioners at start (2021 - census)):
- pension age = 65
- number of pensioners = 2,148,048
Policy variables
- retirement age = 65
- employee social insurance contribution (percentage) (2021) = 6,5%
- employer social insurance contribution (percentage) (2021) = 25%
- inflation clause:
- inflation clause starting point = yes
Economic variables
- Average Gross Wage:
- average wage starting point 2021 = 37 839 Kč
- Average Pension:
- average pension starting point 2021 = 15 425 Kč/month
Fiscal variables
- unemployment rate:
- average unemployment = 5.44% (1993 – 2023)
Random variables To incorporate a realistic level of variability into the population model, stochastic behavior was added to five key rates: fertility, mortality, growing up,retirement and average inflation. Instead of treating these rates as fixed constants, their values are drawn from probability distributions during each simulation run (or time step), based on historical averages and standard deviations.
- fertility rate:
- fertility average: 0.89%
- fertility standard deviation: 9.584343067×10^(-4)
- mortality rate:
- mortality average: 0.65%
- mortality standard deviation: 3.014130177×10^(-3)
- retirement rate:
- retirement average: 1.26%
- retirement standard deviation: 1.684852281×10^(-3)
- growing up rate:
- This variable simulates the transition of children into the working-age population at age 20. For the first 20 years, it mirrors the fertility rate, assuming minimal mortality. After 20 years, the model transitions to using the exact number of births from prior simulated years to determine the number of adults entering the workforce.
- average inflation:
- median inflation: 2.50%
- standard deviation: 0.035619722281127
- Due to significant fluctuations in historical inflation data, including extreme values (e.g., 15.1% in 2022), the median was chosen over the mean to reduce the impact of outliers.
Variables Vensim
Stock
- Childrens = INTEG ( birth - grown up, 2.1816e+06 )
- Working-age Population = INTEG ( growing up - retired, 6.19452e+06 )
- Pensioners = INTEG (retiring - deaths, 2.14805e+06 )
- Average Gross Wage = INTEG ( gross wage increase - gross wage reduction, 37839 )
- Average Pension = INTEG ( valorization of pension - pension reduction, 15425)
- Pension System Annual Balance = ( social insurance – pension, 1 )
Variables
- birth = population*fertility rate
- grown up = IF THEN ELSE(simulation time >= 20, fertility rate history * population history, population * growing up rate)
- growing up = grown up
- retired = population*retirement rate
- retiring = retired
- deaths = population*mortality rate
- retirement age = 65
- employee social insurance contribution (percentage) = 0.065
- employer social insurance contribution (percentage) = 0.25
- inflation clause = 0.5
- gross wage increase = Average Gross Wage * 0.3 * average inflation
- gross wage reduction = PULSE( gross wage reduction year, 1) * gross wage reduction amount
- valorization of pension = Average Pension * inflation clause * average inflation
- pension reduction = PULSE( reduction year , 1 ) * pension reduction amount
- social insurance = yearly contribution
- pension = Pensioners * Average Pension
- yearly contribution = ("Working-age Population" * (1 - unemployment rate)) * Average Gross Wage * ("employee social insurance contribution (percentage)" + "employer social insurance contribution (percentage)")
- unemployment rate = 0.0544
- fertility rate = RANDOM NORMAL(0, 0.05, 0.0089, 0.000958434, 888)
- mortality rate = RANDOM NORMAL(0, 0.05, 0.0065, 0.00301413, 999)
- average inflation = RANDOM NORMAL(0, 0.15, 0.025, 0.0356197, 999)
- retirement rate = RANDOM NORMAL(0, 0.03, 0.0126, 0.00168485, 999) * (IF THEN ELSE( retirement age > 65, 1 -0.004 * (retirement age - 65), IF THEN ELSE( retirement age < 65, 1 + 0.004 * (65 - retirement age), 1)))
- growing up rate = RANDOM NORMAL(0, 0.05, 0.0089, 0.000958434, 888)
- fertility rate history = DELAY FIXED(fertility rate, 19, 0)
- population history = DELAY FIXED(population, 19, 0)
- simulation time = INTEG (1, 1)
- population = Childrens+Pensioners+"Working-age Population"
- gross wage reduction amount = 0
- gross wage reduction year = 1
- pension reduction amount = 0
- reduction year = 1
- ratio of workers to pensioners = "Working-age Population"/Pensioners
Results
In next section I runned simulation multiple times with different parameters to see if there is setup which can lead to sustainable pension system.
Run 1
Parameters
- all default
Result
- Pension system went to negative numbers in year: 40
- Zhodnocení
Run 2
Parameters
- retirement age = 70
Result
- Pension system went to negative numbers in year: 42
- Zhodnocení
Run 3
Parameters
- retirement age = 75
Result
- Pension system went to negative numbers in year: 43
- Zhodnocení
Run 4
Parameters
- employee social insurance contribution (percentage) = 0.08 (8%)
- employer social insurance contribution (percentage) = 0.28 (28%)
Result
- Pension system went to negative numbers in year: 46
- Zhodnocení
Run 5
Parameters
- inflation clause = 0 (without valorization / pension freeze)
Result
- Pension system went to negative numbers in year: N/A
- Zhodnocení - we can see based on ratio of workers to pensioners that the balance is increasing slower and slower and in the future the system will fail if this ratio doesnt stop decreasing
Run 6
Parameters
- inflation clause = 0.1 (10% valorization)
- retirement age = 75
Result
- Pension system went to negative numbers in year: N/A
- Zhodnocení - same as run 5 but balance start slowly decreasing and system will fail sooner than in run 5
Run 7
Parameters
- inflation clause = 0 (without valorization / pension freeze)
- employee social insurance contribution (percentage) = 0.08 (8%)
- employer social insurance contribution (percentage) = 0.28 (28%)
- retirement age = 75
Result
- Pension system went to negative numbers in year: N/A
- Zhodnocení - By far the strongest setting of system but its not sustainable in real world. Also it fails when number of working population really lower.
Run 8
Parameters
- pension reduction amount = 10 000
- reduction year = 40
Result
- Pension system went to negative numbers in year: 42
- Zhodnocení - reduction of pension amount only postpone inevitable collapse of pension system
Result First think we can see that every simulation end with ratio of workers to pensioners less than 1.
If we want to postpone failure of pension system it would be optimal to pick parameters for example from run 6 but in the end all of the setups will fail in time because of decreasing ratio of workers to pensioners and in this system pensioners relies on working age population.