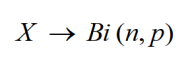Binomické rozdělení

Přemýšleli jste někdy o tom, jak předpovědět počet úspěchů v sérii nezávislých pokusů? Nebo jste možná zvědaví na pravděpodobnost dosažení konkrétního výsledku v sekvenci otázek s odpověďmi ano/ne? Pokud ano, hovoříme v podstatě o binomickém rozdělení, které se vztahuje k binomickým experimentům (tj. s binárními výsledky). Binomické rozdělení je důležitým konceptem v oblasti datové vědy a často se používá v rámci podnikových aplikací.

Úvod

Pravděpodobnostní rozdělení pro experiment s mincí. Počet pokusů = 10 a pravděpodobností úspěchu (pád orla při jedném hodu) = 0,5.

Přemýšlejme o následujících experimentech a náhodných veličinách:

1. Házíme 10krát mincí. Označme počet kolikrát padne orel.
2. Stroj vyrábí díly a některé z nich jsou vadné. Označme jako počet vadných dílů ze 100 z nich náhodně vybraných.
3. Z celkového počtu pacientů trpících konkrétním onemocněním 35 % zažije zlepšení díky určitému léku. U následujících 1000 pacientů, kterým je podán ten samý lék, označme jako počet pacientů, kteří zpozorují zlepšení.
4. Test obsahuje 10 otázek s více možnými odpověďmi, každá s čtyřmi možnostmi, a vy hádáte u každé otázky. Označme jako počet správně zodpovězených otázek.

Každý z těchto náhodných experimentů si lze představit jako soubor opakovaných náhodných pokusů: 10 hodů mincí nebo třeba 1000 pacientů užívajících lék. Náhodná veličina je počet pokusů, které splňují určité kritérium. Výsledek každého pokusu buď splňuje kritérium, nebo ne; proto lze každý pokus shrnout jako „úspěch“ nebo „neúspěch“. Například v experimentu s testem je pro každou otázku pouze jedna kombinace možností, která je správná, a tedy považována za úspěch.

Termíny „úspěch“ a „neúspěch“ jsou pouze označení. V případě experimentu 2 je vyrobení vadného dílu označováno jako „úspěch“, protože počítá vadné díly. Stejně dobře můžeme použít označení „A“ a „B“ nebo „0“ a „1“.

Terminologie

Binomický experiment

Nebo také Bernoulliho experiment/Bernoulliho schéma jsme si v úvodu představili, pojďme si ho nadefinovat a formalizovat.

Požadavky

Požadavky pro to, aby náhodný experiment byl binomickým experimentem, jsou následující:

• Pevný počet (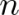) pokusů.
• Každý pokus musí být nezávislý na ostatních. (výsledek jednoho pokusu nemá žádný vliv na výsledek ostatních pokusů.)
• Každý pokus má právě dva možné výsledky, nazývané "úspěch" (výsledek, který nás zajímá) a "neúspěch".
• Existuje konstantní pravděpodobnost (pravděpodobnost, že pokus skončí „úspěchem“, je stejná v každém z pokusů) (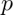) úspěchu pro každý pokus, přičemž doplňkem této pravděpodobnosti je pravděpodobnost „neúspěchu“, která se někdy označuje jako .

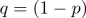Náhodná veličina

Pro definici binomického rozdělení začneme s definicí náhodné veličiny . Tu lze jednoduše definovat jako číselné vyjádření výsledku náhodného jevu.

Binomická náhodná veličina

V binomických náhodných experimentech je počet „úspěchů“ v n pokusech náhodný. Může nabývat celočíselných hodnot od 0, pokud všechny pokusy skončí „neúspěchem“, nebo může být tak vysoký jako je , pokud všechny pokusy skončí „úspěchem“. Náhodná proměnná , která reprezentuje počet „úspěchů“ v těchto pokusech, se nazývá binomická náhodná veličina a je určena hodnotami a .

Definice

Binomická náhodná veličina je definována jako počet výskytu události (úspěchů) v Bernoulliho pokusech. To, že má náhodná veličina binomické rozdělení zapisujeme:

Příklad: Binomické nebo ne?

Zvažme ještě několik náhodných experimentů. U každého z nich rozhodneme, zda je náhodná proměnná binomická. Pokud je, určíme hodnoty pro a . Pokud není, vysvětlíme proč.

Příklad A

Házíme spravedlivou kostkou 50krát; je počet krát, kdy padla šestka.

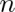je binomická s = 50 a 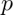= 1/6.

Příklad B

Opět házíme spravedlivou kostkou, je počet hodů potřebných k dosažení šestky.

není binomická, protože počet pokusů není pevně stanovený.

Příklad C

Vybíráme náhodně 3 karty jednu po druhé, nevracíme je zpátky do balíčku, z klasické sady obsahující 4 druhy karet. je počet vybraných karet se znakem srdce.

není binomická, protože výběry nejsou nezávislé. (Pravděpodobnost úspěchu (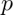) není konstantní, protože je ovlivněna předchozími výběry.)

Příklad D

Odpovídáme na 10 testových otázek zcela náhodně, prvních pět otázek je ano/ne a druhých pět otázek má čtyři možnosti, ze kterých je jedna správná. představuje počet správných odpovědí.

není binomická, protože pravděpodobnost 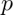se mění z 1/2 na 1/4.

Příklad E

Pravděpodobnost mít krevní skupinu B je 0,1. Vybíráme 4 náhodné osoby. je počet osob s krevní skupinou B.

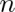je binomická s = 4 a 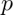= 0,1.

Komentář: Při výběru relativně malé náhodné vzorky (4 osoby) z velké populace, i když se odběr provádí bez „náhrady“, můžeme předpokládat nezávislost, protože matematický vliv odstranění jednoho jedince z velké populace na další výběr je zanedbatelný.

Binomické pravděpodobnostní rozdělení

Nyní je čas diskutovat o pravděpodobnostním rozdělení binomické náhodné veličiny. Začneme jednoduchým příkladem a poté se přesuneme k obecnému vzorci.