Monte Carlo method application in simulations/cs

Úvod

Metodu Monte Carlo lze uplatnit v řadě simulací různého typu ať z oblasti hazardních her, projektového managementu, financí, pojišťovnictví, techniky či například i matematiky. Některé oblasti použití jsou blíže vysvětleny níže v tomto textu. Tuto metodu lze využít především v simulacích, ve kterých je řešení problému jistým způsobem závislé na pravděpodobnostech. Podstatou této metody je generování velkého počtu scénářů pomocí pseudonáhodných čísel. Tato pseudonáhodná čísla jsou generována na základě pravděpodobnostního rozdělení, které vychází z historických údajů nebo ze znalostí a zkušeností expertů, kteří dobře rozumí povaze rizikových faktorů. Metoda Monte Carlo tedy vnáší do modelu náhodou veličinu, která vyjadřuje to, že budoucnost se může od minulosti nějakým způsobem vychýlit.

Metoda Monte Carlo vyžaduje po zainteresovaných stranách, aby hlouběji přemýšleli nad jednotlivými rizikovými faktory. Velmi důležitým krokem je také stanovení rozdělení pravděpodobnosti daných rizikových faktorů, které není vždy snadným úkolem. Toto rozdělení bývá většinou stanoveno na obecných vlastnostech či expertních analýzách.

Postup při simulaci Monte Carlo

Než začneme provádět simulaci, je důležité si ujasnit otázku, na niž pomocí simulačního modelu budeme hledat odpověď. Dalším důležitým krokem je určení základních částí modelu a zajištění, aby těmto částem rozuměly všechny zainteresované strany. V případě, že by došlo k nepochopení, mohl by nastat problém v pozdějším zamítnutí čí požadavku na přepracování, čemuž je samozřejmě nejlepší předcházet. K lepšímu pochopení nám může pomoci tzv. influenční diagram viz. obrázek 1, který umožňuje jasně a přehledně zachytit základní prvky simulačního modelu a jejich vzájemné vazby.

Pro snazší orientaci a pochopení je dobré rozlišovat mezi hlavními prvky influenčního diagramu. Je důležité rozeznávat:

• proměnné, jejichž hodnotu můžeme (do určité míry) ovlivnit,
• rizikové faktory, které nemůžeme přímo ovlivnit,
• kriteriální proměnnou, tedy proměnnou, kterou chceme pomocí modelu analyzovat.

Vzájemné vazby mezi prvky modelu značíme šipkami. Lze také modelovat více úrovní diagramu například náklady můžeme rozdělit na fixní a variabilní, marketingové výdaje na online a offline atd.

Pokud všechny zainteresované strany rozumí základním prvkům modelu, vazbám mezi nimi a cíli modelu, lze začít sestavovat model například v nástroji MS Excel, který se následně rozšíří o simulace Monte Carlo.

Simulaci Monte Carlo lze rozdělit do několika kroků:

1. Stanovení cíle

Nejdříve je důležité jasně definovat, čeho má být dosaženo a pomocí jakých veličin (například zisk, marže atd.).

2. Tvorba deterministického matematického modelu

V dalším kroku sestavíme deterministický matematický model, který by měl popisovat určitou reálnou situaci, měl by ji skutečně vyjadřovat, ale zároveň by neměl být příliš složitý. Tento model se vyznačuje tím, že v něm nalezneme pouze nenáhodná čísla. Při tvorbě modelu je nutné dbát na rozdělení vstupních a výstupních veličin.

3. Tvorba stochastického modelu

V tomto kroku vytvoříme stochastický model, který se bude od deterministického lišit v tom, že některé parametry uvažujeme jako náhodné veličiny. Tento model se přibližuje reálným dějům, ve kterých je náhodná veličina také obvykle přítomná. Nelze říci, že stochastický model odpovídá reálné situaci zcela přesně, ale s určitou pravděpodobností. Výstupem modelu je funkce náhodných veličin a konstant.

4. Určení klíčových rizikových faktorů

Dalším důležitým krokem je stanovení rizikových faktorů, tedy těch veličin, které budou významně ovlivňovat nejistotu výstupů simulace. Mezi těmito faktory jistě budou takové, na jejichž změny jsou výstupy simulace značně citlivé.

5. Stanovení rozdělení pravděpodobnosti klíčových rizikových faktorů

K zajištění úspěšného použití metody Monte Carlo je nezbytné správně určit rozdělení pravděpodobností rizikových faktorů. V předchozím kroku jsme identifikovali klíčové rizikové faktory a nyní pro ně musíme stanovit rozdělení pravděpodobnosti. U diskrétních faktorů rizika (faktory s několika málo hodnotami) má rozdělení pravděpodobnosti tabulkový tvar a u spojitých rizikových faktorů se běžně volí určitý typ rozdělení a zadávají se jeho parametry. V případě, že máme k dispozici historická data určitého faktoru, můžeme využít ke stanovení jeho rozdělení aproximace nějakým teoretickým rozdělením. Pokud historická data k dispozici nemáme, je nutné vycházet ze znalostí a zkušeností expertů, kteří dobře rozumí povaze rizikových faktorů.

6. Stanovení statistické závislosti rizikových faktorů

Nesmíme opomenout, že některé rizikové faktory mohou být závislé na některých jiných faktorech. V případě, že nějakou závislost zjistíme, je důležité ji při simulaci respektovat, jinak by výsledky simulace byly zkreslené. Příkladem statistické závislosti je například poptávka po určitém zboží, která může být závislá na prodejní ceně tohoto zboží, pokud cena stoupá, poptávka po tomto zboží klesá a naopak.

7. Provedení simulace pomocí počítačového programu

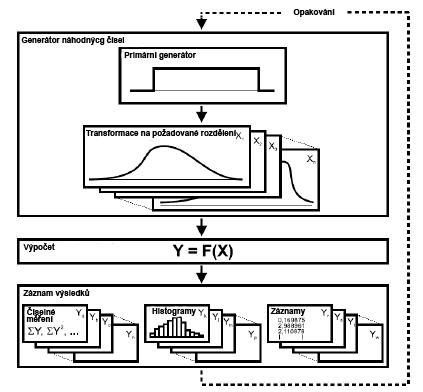
Počítačový program (například MS Excel, Crystal Ball, Matlab, ModelRisk atd.) provádí velký počet scénářů, které se opakují až do konce simulace. Konec simulace nastává provedením posledního scénáře ze stanoveného počtu. V každém simulačním kroku jsou programem vygenerovány možné hodnoty rizikových faktorů z jejich rozdělení pravděpodobnosti a je propočteno výstupní kritérium. Každý tento simulační krok neboli scénář odpovídá jednomu možnému vývoji reálné situace. Po proběhnutí dostatečného počtu simulačních kroků dostaneme výsledky, které mohou být interpretovány jak graficky tak i číselně. Graficky mohou být výstup interpretovány například pomocí histogramu, funkce hustoty či pomocí číselných charakteristik, kterými jsou průměr, medián, horní, dolní kvartil atd.

Obrázek 2: Schéma postupu metody Monte Carlo, zdroj: