Výroba elektřiny fotovoltaickými panely

Tato stránka slouží jako výzkumná zpráva simulace "Výroba elektřiny fotovoltaickými panely pro pokrytí denní spotřeby v celoročním provozu" k semestrálnímu projektu pro předmět 4IT495 Simulace systémů (LS 2014/2015) na VŠE v Praze (Fakulta: FIS, Katedra: KIT, Obor: Kognitivní informatika).

Zadání

• Název simulace: Výroba elektřiny fotovoltaickými panely pro pokrytí denní spotřeby v celoročním provozu

• Předmět: 4IT495 Simulace systémů (LS 2014/2015)

• Autor: Bc. Ondřej Cahlík, xcaho01

• Typ modelu: Monte Carlo

• Modelovací nástroj: MS Excel

Definice problému

Simulace se zabývá řešením problému maloodběratele elektrické energie, tj. domácnosti, která chce být nezávislá na centrálních dodavatelích a elektřinu si chce vyrábět samostatně prostřednictvím fotovoltaických panelů. Problémem je určení potřebného počtu panelů o specifickém výkonu, které dokážou pokrýt denní spotřebu chaty či domácnosti při celoročním provozu. Systém výroby/spotřeby je řešen tak, že domácnost disponuje dvojicí baterií, přičemž z jedné baterie je energie spotřebiči čerpána a druhá baterie je panely dobíjena. Pro účely simulace není podstatné, která baterie je aktuálně nabíjena a která vybíjena, ale zajímá nás potřebná kapacita baterie. Jedna baterie by měla být schopna nepřetržitě (bez dobíjení) zásobovat domácnost elektřinou alespoň 7 dní. Týden je doporučovaná záloha při celoročním provozu z důvodu nevyzpytatelnosti počasí. V průběhu celého roku by měly být panely schopny na denní bázi dobít baterii alespoň do výše spotřebované energie. Případy, kdy je spotřeba vyšší než výroba jsou vyrovnávány díky cca 7x vyšší kapacitě baterií, než činí průměrná denní spotřeba. V některé dny se vyrobí naopak více energie, než je spotřebováno, což tvoří kapacitní zisky. Baterie tedy slouží jako zásobník, který kompenzuje výkyvy ve výrobě i spotřebě.

kapacitě baterií dobít druhou baterii denně vyrobit tolik elektřiny

Jde o zálohu z důvodu nevyspitatelnosti počasí

nicméně v simulaci je zjišťována průměrná týdenní spotřeba domácnosti.

což se střídá v závislosti na úrovni nabití jednotlivých baterií.

Energie je čerpána z dvojice baterií, každá z baterií by měla

Ve své simulaci se budu zabývat zodpovězením otázky - kolik je nutné pořídit fotovoltaických panelů k nabíjení baterie, která pokryje denní spotřebu chaty či domácnosti při celoročním provozu. Nejprve bude určena spotřeba a k tomu potřebná kapacita baterie. Poté předpokládaný výkon panelů v průběhu roku v závislosti na podmínkách prostředí (počasí, délka slunečního svitu). Panely v souhrnu (ve zjišťovaném počtu) musí být v průběhu celého roku schopny dodávat energii tak, aby dobily baterii alespoň do úrovně denní spotřeby elektrické energie.

Cíl simulace

Simulace by měla pomoci v rozhodnutí, jak nastavit systém benefitů a slev, případně potvrdit jeho správné nynější nastavení.

Otázky

Měl by majitel zvyšovat slevy, aby dosáhl větších zisků? Vyplatí se mu dárky, když může nabízet slevy a ušetřit si starosti? Měl by nabízet i slevy větší než 10%?

Metoda

Tato úloha je typická pro řešení metodou Monte Carlo, kterou jsem řešil pomocí programu MS Excel 2007, který pro mě byl nejdostupnější.

Model

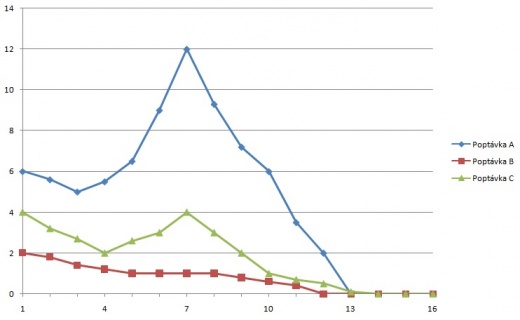
Majitel eshopu se zabývá prodejem třech značek hodinek. Podle dostupných dat jsem zjistil, že po jednotlivých značkách je rozdílná poptávka, viz. obrázek níže. Horizontální osa koresponduje s cenovými kategoriemi hodinek použitými v simulaci, vertikální vyjadřuje počty koupených hodinek.

Poptávky jsem využil k vytvoření závislostí mezi poskytnutou slevou a zvýšením počtu objednávek. Hodinky samotné jsou rozděleny do cenových kategorií jednak podle slev, které na ně prodejce při koupi poskytuje (viz. výše), a také tak, aby byly kategorie smysluplné vzhledem k ostatním. K výpočtu průměrné ceny je použit vážený průměr cen všech hodinek v dané kategorii.

Z dat jsem rovněž vypočítal průměrnou poskytnutou slevu (tzn. "klasickou" slevu a slevu 10%, kterou majitel poskytuje jen někdy, ve váženém průměru). Pro výpočet nákladů využívám dat ke stanovení pravděpodobnosti, že si zákazník vybere dárek/slevu na zakoupené zboží, to se pak rozhoduje pomocí funkce RAND(). Stejně se rozhoduje i to, zda zákazník bude požadovat zaslání zboží (a tedy další náklad ve formě poštovného), nebo si jej vyzvedne osobně.

Parametry modelu

• Výnosy
• Fixní náklady
• Náklady na dárky
• Slevy
• Zisk
• Množství položek v cenové kategorii
• Průměrná cena v kategorii
• Vážená průměrná poskytnutá sleva při nákupu
• Pravděpodobnost, že zákazník zvolí dárek/slevu

Výsledky

Základní data s náhodnou veličinou byla interpretována na 30 000 řádcích tabulky, z toho získaná data byla následně přetransformována do sloupců podle výše jednotlivých slev a toho, zda prodejce při poskytování slev zároveň poskytuje i dárky, a z nich vypočítán zisk, který prodejce poskytnutí dané slevy, spolu s odpovídajícím nárůstem objednávek, přinese. Posledním sloupcem v tabulce je sloupec, ve kterém prodejce naopak neposkytuje slevy, ale k hodinkám poskytuje pouze dárky.

Na obrázku níže je vybraný vzorek z provedené simulace, 15 řádků, na kterých je nastaveno automatické formátování v MS Excel tak, aby byly zvýrazněny všechny hodnoty v řádku, které jsou vyšší než původní získ. Zajímavé je, že původní zisk v tomto vzorku třikrát překonala i možnost, ve které majitel neposkytuje slevy.

Na obrázku níže, je náhodný vzorek z provedené simulace, 15 řádků, na kterých je nastaveno automatické formátování v MS Excel tak, aby byly zvýrazněny tři nejvyšší hodnoty. Zde se ve dvou případech prosadil stávající model (dárky a slevy) se slevami šest a sedm procent a jednou model bez dárků s šestiprocentní slevou.

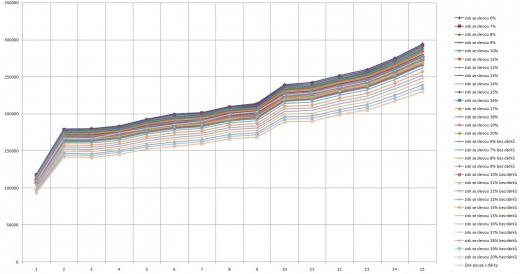
Na obrázku níže je graf pro výše uvedený vzorek slevových funkcí z provedené simulace.

Závěr

Odpovědi

Z výsledků simulace vyplývá, že nastavený model, při optimálnějším nastavení, bude fungovat. Majitel obchodu by měl pro zvýšení zisků zvýšit poskytované (a proklamované) slevy na šest, či sedm procent a sledovat, zda praxe potvrdí nasimulované zvýšení zisků.

Co se týče navrhovaného zrušení dárků, není to podle mě vhodná strategie, i když může přinést vyšší zisk, než který má prodejce nyní (spolu se zvýšením slev). Možnost zvolit si dárek však může být pro zákazníky důležitá i v jiných ohledech, přinejmenším jim dává možnost volby. Spíše by stálo za snahu, domluvit lepší nákupní ceny dárků a tím snížit své náklady.

Poslední otázku, týkající se zavedení slev nad 10%, bych zodpověděl tak, že ne. Při slevách nad 10% se již simulace dostává relativně blízko výchozímu zisku a to pouze při využívání dárků. Při jejich zrušení by se stala meta deseti procent slevy již prodělečnou. Pro maximalizaci zisku bych využil menší slevy, konkrétně šest až sedm procent.

Kód

Simulace v .xlsx formátu má přes 50 MB, rozdělil jsem ji tedy do dvou archivů a ještě pro jistotu nahrál na uloz.to .