Normální rozdělení
Contents
Úvod
Normální rozdělení a jeho varianta normované normální rozdělení patří spolu s rovnoměrným rozdělením a exponenciálním rozdělením mezi spojitá pravděpodobností rozdělení. Alternativně se nazývá také Gaussovo rozdělení, podle německého matematika a fyzika Carla Friedricha Gausse, který ho jako první popsal. Jedná se o jedno z nejdůležitějších pravděpodobnostních rozdělení, neboť lze pomocí něho popsat mnoho jevů vztahující se na člověka a další živočichy a ve statistice se používá pro aproximaci jiným pravděpodobnostních rozdělení.
Definice
Náhodná veličina X má normální rozdělení N(μ,σ²) právě tehdy, když má hustota pravděpodobnosti tvar:[1]
Kde µ je střední hodnota a σ² je směrodatná odchylka. Střední hodnota udává, v jakém bodě křivka dosahuje nejvyšší hodnoty a směrodatná odchylka udává sklon křivky na obou stranách. Grafem hustoty pravděpodobnosti je zvonovitá křivka, symetrická kolem střední hodnoty µ. Všichni jí znají pod pojmem Gaussova křivka.

Někdy se místo normálního rozdělení používá normované normální rozdělení, což je speciální případ normálního rozdělení, které má střední hodnotu rovnou 0 a směrodatnou odchylku rovnou 1.

Lépe představitelnou interpretací normálního rozdělení jsou vztahy, které uvádějí pravděpodobnosti různých intervalů kolem střední hodnoty rozdělení.
- V rozmezí hodnot µ ± 1σ se vyskytuje 68,3 % všech jedinců populace.
- V rozmezí hodnot µ ± 2σ se vyskytuje 95,5 % všech jedinců populace.
- V rozmezí hodnot µ ± 3σ se vyskytuje 99,7 % všech jedinců populace.

Vzorce
Pravděpodobností funkce: 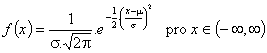 [1]
[1]
Distribuční funkce: 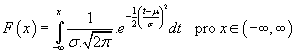 [1]
[1]
Reálné aplikace
Jak bylo zmíněno výše tak normální rozdělení popisuje mnoho jevů týkajících se člověka, jako například jeho výšku, inteligenční kvocient, velikost nohy, nebo porodní váhu.

Na tomto obrázku z roku 2011 můžeme vidět rozdělení výšky žen a mužů v USA. Obě křivky téměř dokonale kopírují Gaussovu křivku. Pokud by se někomu podařilo získat údaje o výšce všech obyvatel země, tak by křivky měli totožný tvar, jen by měli odlišnou střední hodnotu a směrodatnou odchylku. V Současnosti by střední hodnota byla vyšší, v důsledku neustálého růstu průměrné výšky v populaci.
Mezi nejznámější případy použití normálního rozdělení je popsání rozdělení inteligenčního kvocientu (IQ) u člověka, které lze popsat normálním rozdělením se střední hodnotou 100 a směrodatnou odchylkou 15. Tento obrázek snad viděl každý, kdo se alespoň trochu zajímal o normální rozdělení, nebo IQ.

Některé náhodné jevy také mohou generovat normální rozdělení. Vezměme si například hod mincí, kde pravděpodobnost pro obě strany mince je 50 %. Pokud ale budeme mincí házet opakovaně a zaznamenávat počet bodů pro strany mince, tak například při 6 opakováních hodů mincí s největší pravděpodobností bude výsledek 3 body pro každou stranu mince. A graf výsledných bodů by měl při velkém množství opakování kopírovat Gaussovu křivku.
Dalším možným využitím je analýza chybovosti výrobků ve výrobních podnicích. Protože člověk nedokáže vyrábět 100 % přesné výrobky dle zadání, tak vznikají odchylky v jednotlivých parametrech hotových výrobků a firma může tyto parametry sledovat a za pomocí normálního rozdělení určit jaká hodnota parametru je ještě přípustná a která už ně. Ve výsledky by jim tedy vznikl graf normálního rozdělení se střední hodnotou v požadované hodnotě parametru a nějakou směrodatnou odchylkou a na základě grafu by mohli rozhodnout jaké je přípustné pásmo a například nastavit kontrolní stroj, aby výrobky, jejichž parametry nejsou v požadovaném pásmu automaticky vyřadí jako vadné. [5]
Nejvíce se však normální rozdělení používá ve statistice k aproximaci ostatních pravděpodobnostních rozdělení. K tomu se využívá Centrální limitní věta. Tato věta v jednoduchosti říká že pokud vezmeme dostatečně velký počet vzorků z jakéhokoliv rozdělení, tak pravděpodobnostní rozdělení středních hodnot z těchto vzorků se blíží normálnímu rozdělení a říká se o něm že je tzv. asymptoticky normální rozdělení. Tohoto se využívá zejména pokud nevíme z jakého rozdělení jsou sledované jevy, nebo se pomocí tohoto aproximují ostatní rozdělení ve statistice.
[6]
Modelový příklad
Zadání Příkladu 1: Výpočet pravděpodobnosti jevu popsaného normálním rozdělením.
Jistá firma se rozhodla podrobit své zaměstnance IQ testu. Průměrná hodnota IQ testu byla 115, směrodatná odchylka 16. Předpokládejme, že hodnoty IQ testu se řídí normálním rozdělením. Určete pravděpodobnost, že hodnota IQ testu při náhodně vybraném zaměstnanci nabude hodnoty:
- a) menší nebo rovné 120,
- b) větší než 105,
- c) v rozpětí 100 až 130.
K výpočtům použijeme MS Excel. Řešení:
- a) Po zadání vzorce NORM.DIST(120;115;16;PRAVDA) do buňky v excelu dostaneme výsledek 0,6227, což po převedení na procenta je 62,27%. Výsledek tedy je, že náhodně vybraný zaměstnanec bude mít hodnou IQ menší než 120 v 62,27 % případů.
- b) Pro výpočet tohoto příkladu využijeme opačného jevu, neboť je to pro výpočet jednodušší. Nejprve tedy vypočítáme hodnotu pravděpodobnosti, že zaměstnanec bude mít IQ menší nebo rovno 105 a tuto hodnotu pak odečteme od 1. Vzorec pro výpočet 1-NORM.DIST(105;115;16;PRAVDA) nám pak vrátí hodnotu 0,7340. Výsledek tohoto příkladu tedy je že v 73,4 % případů bude mít zaměstnanec IQ vyšší než 105.
- c)V tomto příkladě máme spočítat pravděpodobnost intervalu. Nejprve si tedy spočítáme pravděpodobnost jevu, že zaměstnanec má IQ menší než 100 a tuto hodnotu pak odečteme od pravděpodobnosti že Zaměstnanec má IQ menší nebo rovno 130. k dosažení výsledku využijeme vzorec NORM.DIST(130;115;16;PRAVDA)-NORM.DIST(100;115;16;PRAVDA), který nám vrátí hodnotu 0,6515. Výsledek tohoto příkladu tedy je, že s pravděpodobností 65,15 % bude mít náhodný zaměstnanec IQ od 100 do 130 bodů.
Zadání příkladu 2:Výpočet hraniční hodnoty kvartilů normálního rozdělení.
Český statistický úřad posbíral data o výšce občanů vybraného měst. Výška občanů je popsána normálním rozdělením se střední hodnotou 170 cm a směrodatnou odchylkou 15 cm. Jaká je hraniční hodnota pro dolní a horní kvartil výšky obyvatelstva daného města.
- a) Nejprve spočteme dolní kvartil. Hodnotu výšky lze spočítat pomocí inverzní funkce k distribuční funkcí, proto využijeme tento vzorec NORM.INV(0,25;170;15), který nám vrátí hraniční hodnotu při které pravděpodobnost dosáhla 25%. tedy 159,88 cm.
- b) Pomocí stejného vzorce spočítáme i horní kvartil, pouze vyměníme pravděpodobnost za 75 %. Vzorec NORM.INV(0,75;170;15) nám vrátí hodnotu 180,12 cm.
Výsledkem tohoto přikladu tedy je, že 25% občanů je menších než 160 cm a stejné procento občanů je větších něž 180 cm.
Funkce v Excelu
Pro počítání s normálním rozdělením jsou v excelu připravené funkce. Některé z nich byli využiti v modelovém příkladu.
NORM.DIST(x,střed_hodn,sm_odch,kumulativní)
Kde x je hodnota pro kterou chceme zjisti pravděpodobnost výskytu, střed_hodn a sm_odch je střední hodnota a směrodatná odchylka rozdělení a za kumulativní se dosazuje PRAVDA, pokud chceme hodnotu distribuční funkce, a NEPRAVDA, pokud chceme hodnotu hustoty pravděpodobnosti.
NORM.INV(pravděpodobnost, střed_hodn, sm_odch)
Tato funkce vrací hodnotu inverzní funkci ke kumulativnímu normálnímu rozdělení pro zadanou střední hodnotu a směrodatnou odchylku. Jednodušeji řečeno vrátí hodnotu, pro kterou kumulativní normální rozdělení překročí zadanou pravděpodobnost.
Pokud chceme v Excelu použít normované normální rozdělení, tak existují 2 varianty, buď se použijí připravené funkce v Excelu, tedy:
NORM.S.DIST(z,kumulativní) a NORM.S.INV(pravděpodobnost)
Nebo se využijí funkce pro normální rozdělení uvedené výše a zadají se do nich hodnoty 0 pro střední hodnotu a 1 pro směrodatnou odchylku. Výsledky jsou totožné.
Většinu těchto funkcí lze nalézt v Excelu i ve variantě bez teček uprostřed, ale ty byly v novějších verzích excelu nahrazeny funkcemi s tečkami a jsou dostupně pro zpětnou kompatibilitu se staršími verzemi excelu. Výsledky těchto funkcí jsou však stejné, ale je doporučené používat ty novější funkce s tečkami.
Zajímavosti
Normální rozdělení se vyznačuje unikátní vlastností mezi pravděpodobnostními rozděleními, a to tím, že střední hodnota, modus a medián je jedna a tatáž hodnota.
Existuje ještě jedno rozdělení, ve kterém se nachází název normální rozdělení, a to logaritmicko-normální rozdělení. Toto rozdělení je také spojité a s normálním rozdělením sdílí zvonovitý tvar, avšak křivka vždy začíná v 0 a celá se nachází v pravém horním kvadrantu souřadnicové osy.

Logaritmicko-normální rozdělení má např. tělesná hmotnost, délka inkubační doby infekčního onemocnění nebo abundance živočišných druhů. V neposlední řadě toto rozdělení charakterizuje i řadu krevních parametrů, například počet krevních buněk v daném objemu, sérový bilirubin u pacientů s cirhózou. Dále má toto rozdělení také distribuce mezd mezi občany, kdy křivka nezačíná v nule, ale je jakoby uříznuta v hodnotě minimální mzdy, ale pokud bychom si domysleli levý kraj této křivky, tak je to křivka logaritmicko-normálního rozdělení. [8]
Příklady k procvičení
Pro jednoduchost počítejme, že v České republice žije 10 milionů osob. Kolik osob z tohoto počtu trpí oligofrenií(IQ<70) a kolik lidí je geniálních (IQ>140). Inteligenční kvocient je z normálního rozdělení se střední hodnotou 100 a směrodatnou odchylkou 15.
Případné řešení naleznete v tomto Excelu.
Reference
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 OTIPKA, Petr a Vladislav ŠMAJSTRLA. Pravděpodobnost a statistika. Ostrava: Vysoká škola báňská - Technická univerzita Ostrava, 2006. [online]. Dostupné z: https://homel.vsb.cz/~oti73/cdpast1/
- ↑ Pravděpodobnostní rozdělení spojité náhodné veličiny pro základní soubory, Nedatováno. [online] . Dostupné z https://cit.vfu.cz/stat/FVHE/Teorie/Predn2/rozdelZS.htm /
- ↑ Why Sex Differences Don’t Always Measure Up, 2011. . Sugar and Slugs. Dostupné z: https://sugarandslugs.wordpress.com/2011/02/13/sex-differences/
- ↑ 9 Real Life Examples Of Normal Distribution – StudiousGuy, Nedatováno. Dostupné z: https://studiousguy.com/real-life-examples-normal-distribution/
- ↑ Normal Distribution, Nedatováno [online] . Six-Sigma-Material.com. Dostupné z: https://www.six-sigma-material.com/Normal-Distribution.html
- ↑ Central Limit Theorem: Definition and Examples in Easy Steps, Nedatováno [online] . Statistics How To. Dostupné z: https://www.statisticshowto.com/probability-and-statistics/normal-distributions/central-limit-theorem-definition-examples/
- ↑ Nápověda a školení k Microsoft Office, Nedatováno. [Online]. Dostupné z: https://support.microsoft.com/cs-cz/office
- ↑ OTIPKA, Petr a Vladislav ŠMAJSTRLA. Matematická biologie učebnice: Logaritmicko-normální rozdělení, nedatováno [online]. Dostupné z: https://portal.matematickabiologie.cz/index.php?pg=aplikovana-analyza-klinickych-a-biologickych-dat--biostatistika-pro-matematickou-biologii--nahodna-velicina-rozdeleni-pravdepodobnosti-a-realna-data--dalsi-rozdeleni-pravdepodobnosti--logaritmicko-normalni-rozdeleni