RetrieverBreeder
- Project name: RetrieverBreeder
- Class: 4IT496 (WS 2015/2016)
- Author: Bc. Lucie Pokorná
- Model type: Discrete-event simulation
- Software used: SimProcess, trial version
Recommended work outline:
Problem definition - a description of the situation you solve (i.e. the task) Method - the discussion of possible solutions, the selection of method and tools for the solution, reasons for such choice (why the selected methods and tools are the best for the problem) Detailed description of the method, including parameters, ranges, schemes, model limitations, etc. The description must be detailed enough that anybody could replicate the experiment event without your model source codes. Results - list of results, their analysis, interpretation and evaluation. Conclusion - how the problem was solved Citations Model source code (xls, spm, nlogo, mdl, etc. file)
Contents
Problem definition
Simulation should answer the question how many female dogs is optimal to keep for satisfying the demand for golden retriever puppies.
Detailed problem definition
he goal of the simulation is to simulate the whole simplified process to find the optimal amount of female golden retriever dogs owned and/or kept regarding all given variables and facts. Goal is to only have the ideal number of breeding dogs capable to fulfill the given birth giving plan and indirectly let the owner of a cattery satisfy the demand.
Method
When first seeing the SIMPROCESS possibilities and observing the way to show the simulation running, an idea of pet breeding simulation almost immediately came to mind. Such a simulation compound of the generating (literally generating in this case) an entity - puppy delivery, delay - puppy growth and then disposing the entity - either finding a match with a corresponding demand (a waiting customer), offering and older puppy for lower price, or just keeping the particular one in a cattery - is exactly the discrete-event type of simulation that could be shown quite transparently, comprehensible yet clearly enough using this simulation tool.
While the simulation has been conducted, no significant restrictions were found using just a trial version of the program. Few not that necessary activities had to be cut and the rest of the simulation optimized to make sure that the limit for a number of activities is not depriving the simulation of possibly interesting results.
Model
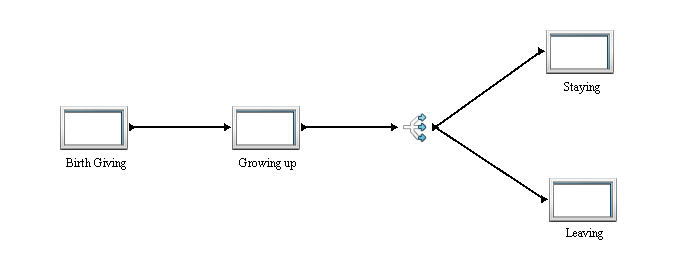
The simulation consists of 4 processes:
- "Birth giving" - puppy generating
- "Growing Up" - delay activity
- "Staying" - the cattery owner decides to keep a puppy
- "Leaving" - ideally a customer picks up a puppy, non ideally puppy is left "unwanted" for a longer period of time and has to be later sold for a lowered price or given entirely
Just one of the processes - the "Leaving" process - contains most of the activities used starting from the probability based division of puppy gender, customer decision making situation and handling an occasional exception - the case when there is no demand for a particular puppy and not even the cattery owner desires to keep it.
The model is based on real data gathered in the stated sources.
The simulation is set to be run in numerous iterations (replications). The more breeding female dogs the cattery owns, the more birth giving occasions there are. For the purposes of this simulation there is no need to simulate breeding dogs in any way, the only thing that is important is the recurrences of such events such is birth givings. It has been decided that each replication will simulate just a one litter had by one female breeding dog. In average, female golden retriever female is capable to give birth once a year and a half when the dog's health and well being is considered a number one priority. Simulation is set to show just a one such cycle. The lasting of a whole simulation including several replications is set to be an exact year and a half. That means that the number of replications equals to number of female breeding dogs within 18 months and actual breeding dogs as en entity or a resource may now be omitted in the simulation.
The distribution function for the demand is set to be invariable in a several runs of a simulation set period of time for a slight simplification. From a personal experience, demand for pedigreed puppies from a particular cattery changes quite a lot, yet the average remains at a very similar level, no matter how many puppies were sold in the past. It is possible and recommendable to adjust the value higher (lower) in a consequent time period - when the time simulated in a simulation passes - when the average demand grows (decreases) based on the actual demand counts have been observed and noted.
Entities
Resources
¨
Processes
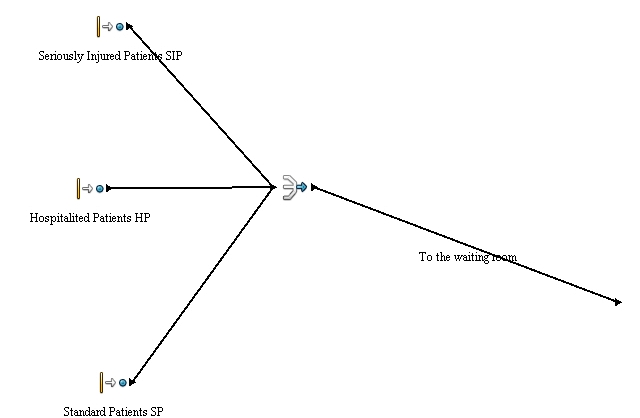
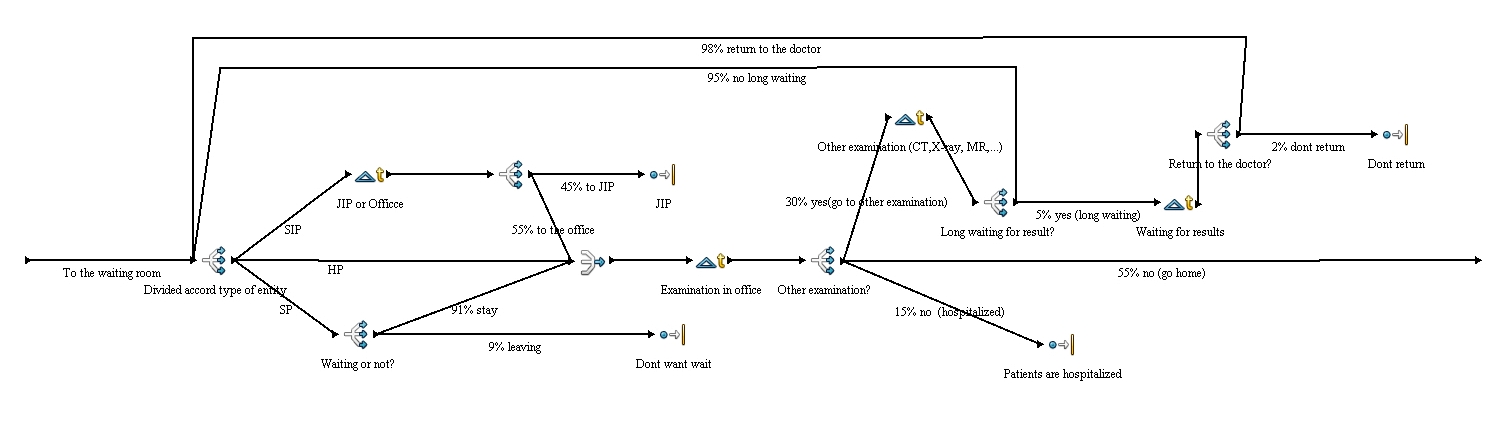
Queue is divided by entities. There is the difference between standard, seriously injured and hospitalized patients. Seriously injured patients (SIP) are preferred over others and they are pre-examined at first. This pre-examination is done by a nurse or a doctor from other staff and is determinative for further procedure. The patient could be sent to the intensive care unit if his injury is really serious (this is around 45% of patients) or he can be sent to the office (this is about 55%). Hospitalized patients have no other branch off. Standard patients are coming from outside of hospital and there is one branch off which is divided by percent. It is because of there are 9%of patients who don’t want to wait and leave the waiting room before an examination by doctor. Other 91% are waiting for an examination by doctor.
This part of simulation simulates examination or treatment by the doctor. It is illustrated by normal distribution Nor(10.0, 3.0, 1) in minutes. In the next step after examination by the doctor it is decided if a patient needs another examination (for example CT, X-ray, MR or other blood tests. There are usually 30% of patients who need another examination. 55% of patients are sent home. And the rest (15%) stays in the hospital and are hospitalized.
This simulates other examinations which are needed for right decisions of a doctor in the office. There is used exponential distribution Nor (15.0, 3.0, 1) minutes. After this patients can be sent back to the waiting room (95%), or can be sent home (5%) because results will be known after 20-23hours. These patients go home, but there are 2% of them who don’t come back to get their results. The rest (98%) comes back for their results. The distribution of the time when they come back is given by triangular distribution Tri (22.0, 23.0, 23.5).
Results
Now we see that we can´t solve problem of waiting time very effectively in real.
The big problem is beginning in the morning. Patients usually start comming at 7:00 and doctors start working at 9:00. There are 2 hours at least when patients have to wait. In both experiments there is maximum count of patients in system around 24 of standard patients, 6 of seriously injured patients and around 7 of hospitalited patients. Maximum number of waiting patients for examination is in case of standard patients around 23.
There is the difference in waiting time between 4 and 2 working doctors in medical staffs. The waiting time is half. But when we count the salary of one doctor (in average around 40 000 -45 000Kč/month) there is situation which is not so economic.
There are limitations as number of staffs in hospital too.
The best solution of this problem is to cut down the lunch break at half hour and start early working.
Conclusion
Making a model of a specific medical staff is quite complicated. It is important to deal with some detailed and unpredictable problems. People(resources) are very unpredictable and system is very complex.
Despite all limitations this simulation can help with optimization of the number of doctors and shows quite real process of patient althought it coud be very complex.