Difference between revisions of "Normal form/cs"
(→Reference) |
(→Reference) |
||
| Line 175: | Line 175: | ||
<div id="link1"><nowiki>[1] </nowiki>SHOHAM, Yoav a LEYTON-BROWN, Kevin. Introduction to Noncooperative Game Theory: Games in Normal Form. 2008. Dostupné online na [http://www.eecs.harvard.edu/~parkes/cs700/gt_chapter.pdf http://www.eecs.harvard.edu/~parkes/cs700/gt_chapter.pdf]. Strana 63.</div> | <div id="link1"><nowiki>[1] </nowiki>SHOHAM, Yoav a LEYTON-BROWN, Kevin. Introduction to Noncooperative Game Theory: Games in Normal Form. 2008. Dostupné online na [http://www.eecs.harvard.edu/~parkes/cs700/gt_chapter.pdf http://www.eecs.harvard.edu/~parkes/cs700/gt_chapter.pdf]. Strana 63.</div> | ||
| − | <div id="link2"><nowiki>[2] </nowiki>ZHENG, Bingyong. Extensive form game. SHUFE Spring, 2011. Dostupné online na [http://bb.shufe.edu.cn/bbcswebdav/institution/%E7%BB%8F%E6%B5%8E%E5%AD%A6%E9%99%A2/teacherweb/2006000057/lecture2.pdf http://bb.shufe.edu.cn/bbcswebdav/institution/%E7%BB%8F%E6%B5%8E%E5%AD%A6%E9%99%A2/teacherweb/2006000057/lecture2.pdf]</div> | + | <div id="link2"><nowiki>[2] </nowiki>ZHENG, Bingyong. Extensive form game. SHUFE Spring, 2011. Dostupné online na [http://bb.shufe.edu.cn/bbcswebdav/institution/%E7%BB%8F%E6%B5%8E%E5%AD%A6%E9%99%A2/teacherweb/2006000057/lecture2.pdf http://bb.shufe.edu.cn/bbcswebdav/institution/%E7%BB%8F%E6%B5%8E%E5%AD%A6%E9%99%A2/teacherweb/2006000057/lecture2.pdf]. Strana 2.</div> |
<div id="link3"><nowiki>[3] </nowiki>BERKA | <div id="link3"><nowiki>[3] </nowiki>BERKA | ||
Revision as of 07:37, 18 June 2014
Normální forma pomocí tabulky nebo matice vyjadřuje užitky hráče v každé z kombinací akcí hráčů. Hráč může mít za cíl maximalizovat zisk nebo minimalizovat náklady. Namísto pojmu normální forma se může používat i pojem normální tvar.
Definice: Hrou v normální formě rozumíme množinu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \{Q, \{X_i\},Z\}}
, kde
|
Contents
Úvod
Ukažme si nejprve, v jakém případě může být normální forma užitečná v teorii her a v běžném životě.
Každý z nás je dennodenně nucen udělat množství rozhodnutí. Některé z nich jsou jednoduché, některé mohou být docela složité. Vybrat si ráno, zda k snídani chcete chléb se šunkou nebo cereálie se sójovým mlékem může být docela jednoduché rozhodnutí. Každý může mít vlastní preference, na základě kterých se dokáže velmi rychle rozhodnout. Situace se může zkomplikovat, pokud chce partner připravit snídani pro sebe i pro svou partnerku, která místo maximalizace energetického příjmu a chuti ve vašem případě preferuje minimalizaci mastných kyselin, rafinovaného cukru a rizika srdečně-cévních problémů. Zároveň je však jednodušší připravit pro oba stejné snídaně, aby se minimalizovalo množství použitého kuchyňského náčiní.. I na řešení takových rozhodovacích problémů zná účinné nástroje teorie her. Právě jsme popsali jednu z nejčastěji používaných modelových her - souboj pohlaví.
| Definice: Teorie her je souborem analytických nástrojů, které nám pomáhají pochopit jevy vznikající při vzájemné interakci rozhodovatele (tj. v situacích, kdy každý rozhodovatel musí brát v úvahu rozhodnutí ostatních rozhodovatele) |
Základním předpokladem při teorii her je, že hráči jsou racionální, to znamená, že si jsou vědomi svých možností a svých preferencí. V našem případě to znamená, že vědí, které potraviny mají nakoupeny a které by právě k snídani upřednostnili. Teorii her je však možné použít i v mnohem komplexnějších rozhodovacích situacích, jako je výběr jídla na snídani.
Rozhodovací situace je charakterizována:
- Možnými akcemi (snídání chleba se šunkou vs. snídání cereálií)
- Užitkem jednotlivých akcí (vysoká energetická hodnota a chuť vs. nutriční hodnoty)
- Preferencemi (partner preferujete chléb, partnerka cereálie)
Hry je možné zapsat ve dvou základních tvarech - normální formě a explicitní formě.
Hry v normální formě
Příklad: V našem případě snídaňové hry:
- Množina hráčů je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Q = \{} partner, partnerkaFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \}}
- Množina jejich tahů je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X = \{} chléb, cereálieFailed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \}}
Věnujme se nyní ohodnocení užitků jednotlivých strategií pro partnera a partnerku.
Užitky můžeme vyčíslit na základě preferencí následovně:
- Partner nejvíce preferuje, aby oba snídali chléb, této možnosti přiřadí hodnotu 3. Druhá nejpreferovanější možnost v pořadí je ta, že partner i partnerka budou jíst cereálie. Partner sice nebude mít nejoblíbenější jídlo, alespoň však bude jednodušší mytí nádobí. Následuje možnost, že on bude jíst chléb a ona cereálie. Nejméně preferovaná možnost je, že on bude jíst cereálie a ona chléb.
- Partnerka nejvíce preferuje, aby oba snídali cereálie, hodnota pro ní v tomto případě bude 3. Následují možnosti, že by oba snídali chléb (2), partner chléb a ona cereálie (1) a naopak, on cereálie a ona chléb (0).
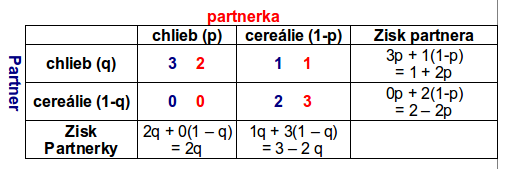
Hru v normální formě můžeme zapsat pomocí matice nebo tabulky. Jelikož se v našem případě jedná o hru neantagonistickú (zisk jednoho hráče nejde na úkor hráče druhého), zapíšeme ji jako dvojmatici nebo tabulku se dvěma hodnotami v každé buňce. Tyto hodnoty budou vyjadřovat hodnoty užitkových funkcí obou hráčů pro všechny možnosti použitých strategií.
Poznámka: Při zápisu do tabulky se používá konvence, že hráč 1 vybírá řádky, hráč 2 vybírá sloupce a případný hráč 3 vybírá tabulku. V našem případě zisky partnera jsou označeny modrou barvou a zisky partnerky červenou barvou.
V modelu normální hry není přítomný čas. Každý hráč vybírá své akcie pouze jednou a současně s ostatními hráči tak, že žádný z hráčů není informován o akci jiných hráčů v momentě, kdy vybírá svou vlastní akci.
Použití normální formy
Pomocí zápisu v normální formě vidíme, respektive víme vyvodit různé závěry o dané hře.
| Úkol: Zamyslete se nad dalšími příklady her a vyzkoušejte si je zapsat v normální formě. Co dokážete z normální formy vyčíst? |
Jaké je tedy řešení souboje pohlaví?
Dominantní a bezpečná strategie
Partneři mohou při řešení postupovat pomocí dvou základních strategií, které lze vyčíst z normální formy:
- Dominantní strategie je ta, při které je zisk daného hráče maximální, bez ohledu na to, jak se zachová partnerka. Pokud se partnerka rozhodne pro chléb, partner by se měl rozhodnout také pro chléb, protože dosáhne užitek 3, naproti nulovému užitku v případě, že by se rozhodl pro cereálie. Pokud se partnerka naopak rozhodne pro cereálie, měl by se i partner rozhodnout pro cereálie, protože v tomto případě by byl jeho užitek 2 naproti užitku 1 v případě, že by se partner rozhodl pro chléb. Pro partnera tedy dominantní strategie neexistuje. Podobně je to i v případě partnerky.

- Bezpečná strategie, jejímž cílem je maximalizovat užitek v nejnepříznivějším případě. Při jejím stanovení hráč postupuje tak, že z minim užitků vybere maximum. V případě partnera, pokud by si vybral chléb, minimální hodnota užitku je 1. Pokud by si vybral cereálie, minimum by bylo 0. Maximum z těchto dvou hodnot je 1, bezpečná strategie pro něj tedy je vybrat si chléb. V případě partnerky, pokud by si vybrala chléb, minimální užitek by měla 0, v případě cereálií 1. Její bezpečná strategie je tedy vybrat si cereálie. Platí tedy, že pro oba je bezpečná strategie vybrat si kombinaci, kdy on bude snídat chléb a ona cereálie.
Je to ale optimální řešení? Kdyby partner změnil své rozhodnutí a snědl by místo chleba cereálie, zvýšil by se jeho zisk z 1 na 2. A kdyby partnerka změnila své rozhodnutí, přineslo by jí to také zisk 2 místo 1.
Nashovo equilibrium
Pokud se partneři rozhodli pro některou ze strategií, otázkou může být, zda se jednomu z nich v dané situaci vyplatí změnit rozhodnutí. Například, pokud se rozhodli pro možnost, že oba budou jíst k snídani chléb, partnerka se může zamýšlet nad tím, zda se jí nevyplatí místo chleba sníst cereálie. Z tabulky normální formy vidíme, že v takovém případě by se jeho zisk snížil z hodnoty 2 na hodnotu 1. Také partner se může zamýšlet, zda-li změní své rozhodnutí, nezvýší užitek. V tomto případě se ale i jeho užitek sníží, a to konkrétně ze 3 na 0. Znamená to tedy, že se jim nevyplatí změnit rozhodnutí. Analogicky by to platilo pro případ, že by se na začátku rozhodli pro možnost chléb, chléb. Říkáme, že tato hra má v těchto dvou možnostech Nashovo equilibrium.
Ověřme ještě opačnou situaci. Řekněme, že se partner rozhodne sníst cereálie a partnerka chléb. V takovém případě bude užitek partnerky 0. Vyplatí se jí tedy změnit rozhodnutí a sníst chléb, protože tak dosáhne zisk 2. A naopak, pokud se partner rozhodne sníst chléb a partnerka cereálie, partnerčin zisk bude 1, vyplatí se jí tedy změnit rozhodnutí a sníst chléb, protože takto by dosáhla zisku 2. V těchto dvou možnostech tedy nenastává rovnováha.
| Úkol: Proč v tomto případě není Nashovo equilibrium v případě strategií (cereálie, chléb)? |
Čistá a smíšená strategie
Pokud hráč volí svou strategii bez jakékoliv náhodnosti, říkáme, že jde o čistou strategii. Pokud by se partner rozhodl namísto racionálního rozhodnutí hodit si mincí, mluvili bychom o smíšené strategii, čili takové, v níž vystupuje prvek náhody. Nemusí však jít přímo o házení mincí. Partner se může rozhodnout vybrat náhodně, pokud si není jistý výběrem partnerky. Smíšené strategie nám však mohou přinést představu o tom, co by se mohlo stát, pokud by se jednalo o opakující se hru. Čili pokud by se partneři před každým večerem rozhodovali znovu a znovu. I pro takový případ dokážeme vypočítat Nashovo equilibrium na základě zápisu v normální formě.
Nashovo equilibrium v smíšené strategii
Náš příklad má však ještě jedno Nashovo equilibrium. Nahoru jsme si ukázali dvě čisté Nashove equilibria. Nicméně existuje ještě jedno equilibrium ve smíšené strategii[1].
Řekněme, že partneři vybírají ze snídaňových možností náhodně. Partnerčina strategie je vybrat si chléb s pravděpodobností p a cereálie s pravděpodobností 1-p. Partner musí být indiferentní k libovolné ze svých možností. Jinak by se mu více vyplatilo vybrat některou z čistých strategií.
Poté platí vztah:
Upartner(chléb) = Upartner(cereálie)
1 + 2p = 2 - 2p
p = 1/4
Partner bude tedy ochoten použít náhodný výběr, pokud si partnerka ve čtvrtině případů bude vybírat chléb a ve třech čtvrtinách cereálie.
Analogicky, partnerova strategie je vybrat si chléb s pravděpodobností q a cereálie s pravděpodobností 1-q. Partnerka musí být indiferentní k libovolné ze svých možností, jinak by se jí více vyplatilo vybrat některou z čistých strategií.
Platí tedy:
Upartnerka(chléb) = Upartnerka(cereálie)
2q + 0(1 – q) = 1q + 3(1-q)
2q = 3 – 2q
q = 3/4
Partnerka bude ochotna použít náhodný výběr, pokud si partner ve třech čtvrtinách případů bude vybírat chléb a v jedné čtvrtině případů cereálie.
Převod mezi normální a explicitní formou

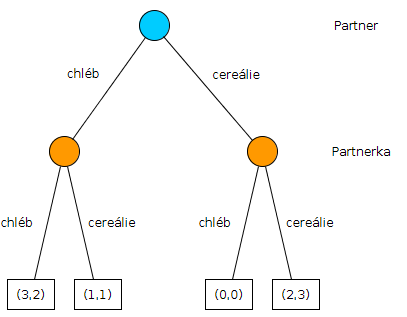
Explicitní i normální forma mohou popisovat stejnou hru. Ukažme si, jak je možné pro hru v normální formě najít její ekvivalent v explicitní formě. Pokud chceme zapsat hru Souboj pohlaví v explicitní formě, zapíšeme ji, jakoby jeden z hráčů provedl tah první a druhý hráč nemá možnost pozorovat tah prvního hráče. Tím zachováme stejnou míru informovanosti ale změníme tahy na sekvenční[2].
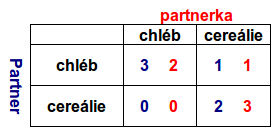
Pokud chceme naopak pro hru v explicitní formě najít ekvivalentní hru v normální formě, postupujeme tak, že si vypíšeme všechny čisté strategie pro každého hráče. Hráč 1 má k dispozici strategie chléb a cereálie. Hráč 2 má k dispozici strategie chléb a cereálie. Do tabulky pak vpíšeme hodnoty ziskových funkcí z listů stromu explicitní formy. Na základě čistých strategií hráčů víme zapsat hru v normální formě:
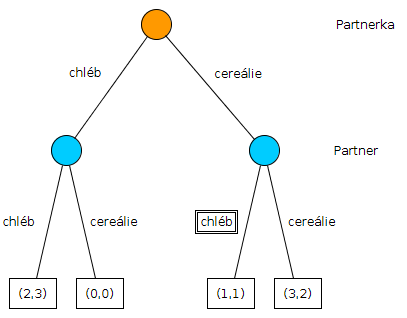
Normální forma poskytuje minimální množství informací potřebných pro popis hry. Dokážeme z ní identifikovat hráče, strategie jednotlivých hráčů a jejich výsledné zisky. Explicitní forma navíc poskytuje informaci o hře co se týče časového pořadí rozhodnutí a množství informací, které je pro hráče k dispozici, když provádějí své akcie. Platí, že každou hru v explicitní formě je možné převést na právě jednu ekvivalentní hru v noromálné formě. Naopak však pro každou hru v normální formě můžeme najít několik možných zápisů v explicitní formě[4]. Například souboj pohlaví bychom v hru explicitní formě mohli zapsat i následovně:
Explicitní forma totiž popisuje i pořadí, v jakém hráči své akcie provádějí. Proto zaměnění partnera za partnerku v prvním uzlu popisujeme již odlišnou hru. Na druhé straně vyměněnu řádků za sloupce v tabulce normální formy ke změně informace nepřichází.