Zatížení sítě Eduroam

Zadání

Název simulace: Zatížení sítě Eduroam a rozložení výuky na vysoké škole

Předmět: 4IT495 Simulace systémů (LS 2013/2014)

Autor: Bc. David Pospíšil

Typ modelu: Monte Carlo

Modelovací nástroj: MS Excel

Definice problému

Model simuluje zatížení sítě Eduroam na Vysoké škole ekonomické v Praze v průběhu jednoho semestru. Díky tomu lze poté vyčíst ideální počet serverů, které jsou nutné pro fungování sítě.

Metoda

Pro simulaci byla použita metoda Monte Carlo v prostředí Microsoft Excel 2013. Tato možnost je ideální proto, že se využívá generování náhodných čísel podle potřebného rozdělení s možností simulace na mnoha tisíců pokusů.

Model

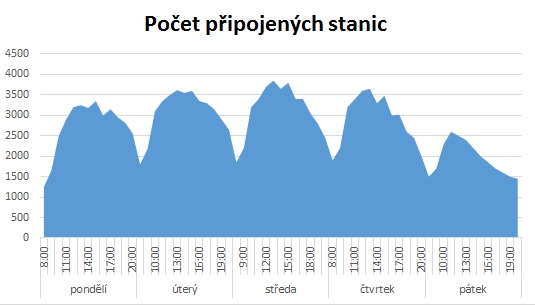
Obr. 1: Počet připojených zařízení podle reálných dat

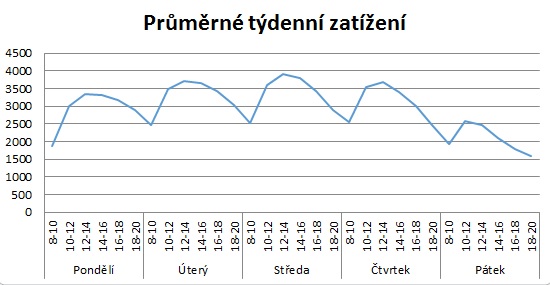
Obr. 2: Průměrné zatížení v rámci týdne na základě generovaných dat

Postup simulace:

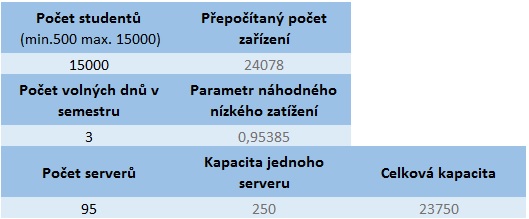
1. Přepočítání celkového počtu zařízení

Po zadání počtu studentů na škole (min 500, max 15000) dojde k přepočtu zařízení tak, že se počet studentů vynásobí koeficientem pro celkový počet zaměstnanců na škole. (Tento koeficient je vypočítán z poměru všech studentů a pracovníků za období 2009 až 2012). Dále se vynásobí poměrem počtu zařízení k počtu uživatelů. Celkové číslo se zvýší o 5% a zaokrouhlí na celé číslo.

2. Výpočet střední hodnoty

V dalším kroku dojde k výpočtu střední hodnoty, směrodatné odchylky, procentuálního zatížení ve dne a procentuálního zatížení v rámci jednoho týdne. To využívá reálných veřejně dostupných dat. Nejdříve se vypočítá procentuální zatížení ve dne tak, že časový interval s nejvyšším zatížením je definován jako 100% a poté jsou dopočítány procentuální zatížení pro všechny ostatní intervaly. Podobně je také vypočítáné i zatížení v rámci týdne, kdy nejvyšší zatížení je (podle reálných dat) ve středu a ostatní dny jsou vůči tomuto dnu relativně odvozeny. Střední hodnoty se počítají jako počet uživatelů násobený procentuální zatížením dne a týdne. Směrodatná odchylka je na základě dlouhodobého pozorování odvozena pro minimum zařízení (803) na 40. Od tohoto čísla je pak relativně vypočítána pro všechna větší čísla.

3. Náhodné generování zatížení

V tomto kroce dochází ke generování náhodných čísel normálního rozložení s tím, že data využívají středních hodnot a směrodatné odchylky vypočítané v předcházejícím kroku. Normální rozdělení je zvoleno proto, že údaje v časových intervalech oscilují rovnoměrně kolem nějaké střední hodnoty s určitou odchylkou. Kromě toho se pro každý den počítá pravděpodobnost, zdali není státní svátek (případně rektorský den či jiné celoškolní volno). Počet svátků může být průměrné číslo za celý rok, ale uživatel si může toto číslo upravit v případě zájmu ve vstupních datech. Toto číslo počítá poměr svátků a celkových dnů za semestr a podle tohoto poměru náhodně snižuje celkové zatížení sítě na 20-60%.

4. Funkčnost serverů

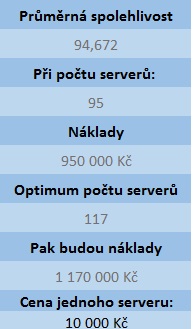
Funkčnost serverů se počítá z předchozí tabulky, která generuje náhodné zatížení a srovnává je s maximální kapacitou serverů zadané uživatelem na začátku. Tabulka počítá pro každý interval, zdali je kapacita dostačující, pokud ano vrátí 1, pokud ne - 0. Díky tomu je pak možné vedle spočítat sumu fungujících serverů za celý semestr (13 týdnů) a vydělit je poměrem všech intervalů - výsledné číslo zobrazuje procentuální spolehlivost za jeden semestr. Tato čísla jsou pak shrnuta v listu "Spolehlivost v týdnech" a díky četnosti zobrazují celkovou procentuální spolehlivost na všech 2308 semestrech.

5. Výpočet optimálních nákladů

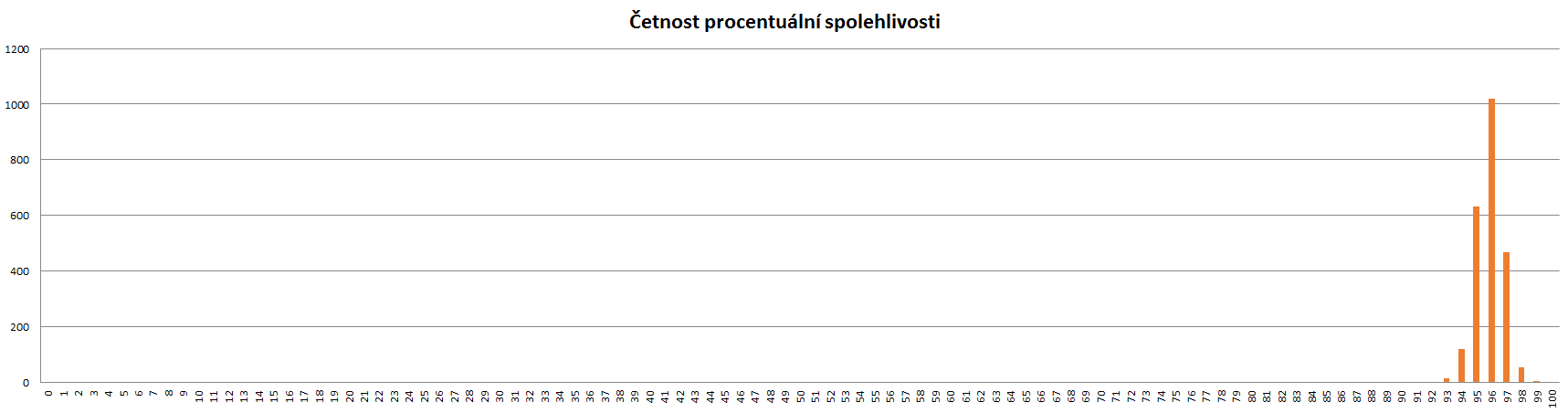
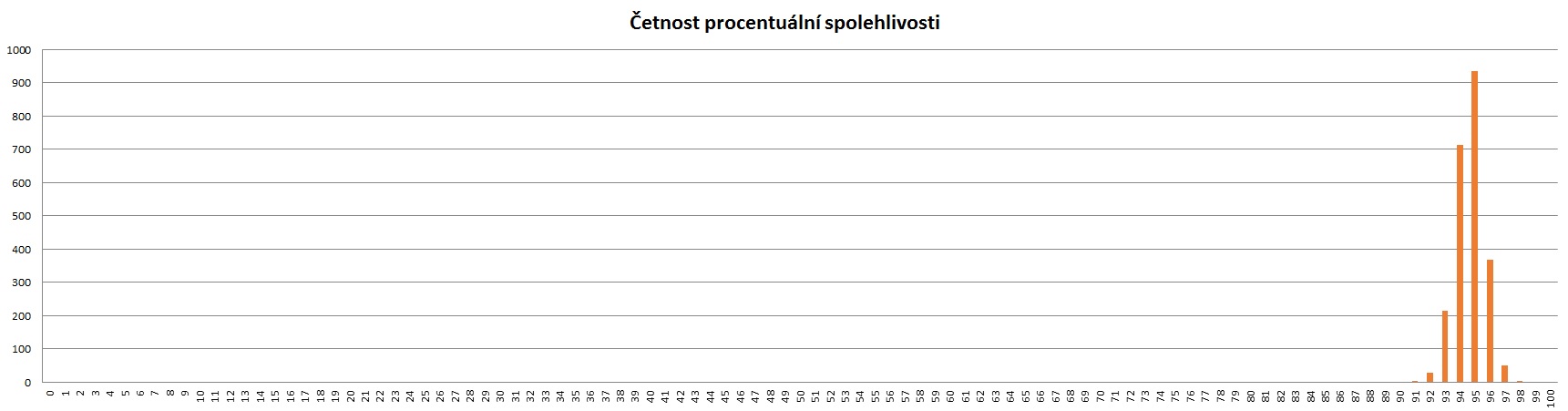
Pro výpočet optimálních nákladu se pro každý interval počítá z podílu celkové kapacity serverů a čísla vygenerovaného pro příslušný interval se zaokrouhlením na čtyři desetinná místa. Z celkové tabulky se najde minimum hodnoty. Následně se vydělí zadaný počet serverů vypočítaným minimem a získané číslo ukazuje nejmenší možný počet serverů pro 100% fungující síť. Záleží už pak na uživateli jakou chybovost je schopen akceptovat a tudíž tento počet sám snížit. Četnost funkčnosti pak může zobrazit na grafu "Četnost procentuální spolehlivosti".

Vstupní parametry:

• Počet studentů
• Počet volných dnů v semestru
• Počet serverů

Listy modelu:

• Vstupní údaje
• Výstup
• Data
• Grafy
• Rozdělení dnů
• Data ve dnech
• Funkčnost serverů
• Náklady pro optimum
• Spolehlivost v týdnech

Výsledky

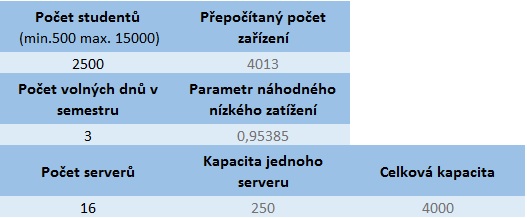
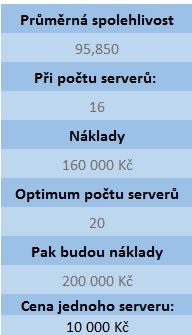
Na základě níže uvedených obrázků lze vidět, že při počtu 2500 studentů přítomných ve škole (odpovídá přibližně odpozorovaným reálným datům) dochází při téměř 96% spolehlivosti k potřebě serverů v za 160 000 Kč. Pokud by bylo žádoucí 100% spolehlivost, cena by vyšplhala na 200 000 Kč. Dále výsledky ukazují maximální možnou kapacitu školy o přítomných 15 000 studentů. Za tohoto předpokladu jsou při spolehlivosti necelých 95% náklady 950 000 Kč, pokud by spolehlivost byla vyžadována opět maximální počet serverů by byl nutný zvednout o 12 a celkové náklady by vyšplhaly na 1 170 000 Kč. Poslední dva grafy zobrazují četnosti procentuální spolehlivosti pro oba pokusy.

Obr. 3 a 4: Vstupní a výstupní parametry pro 2500 studentů ve škole

Obr. 5 a 6: Vstupní a výstupní parametry pro 25 000 studentů ve škole

Obr. 7: Četnost procentuální spolehlivosti pro 2500 studentů

Obr. 8: Četnost procentuální spolehlivosti pro 2500 studentů

Závěr

V modelu se podařilo nasimulovat zatížení sítě Eduroam v jednotlivých dnech po dvouhodinových časových intervalech. Jednotlivých týdnů bylo nasimulováno 30 004 výsledků což odpovídá 2 308 semestrů. Na základě těchto výsledků došlo výpočtu spolehlivosti sítě podle kapacity počtu serverů a tato spolehlivost už závisí na uživateli zdali se mu bude zdát jako dostačující či naopak bude chtít ještě určité zlepšení podpořit dalšími náklady.