Systematické hraní rulety

Zadání

• Název simulace: Systematické hraní rulety
• Předmět: 4IT495 Simulace systémů (LS 2013/2014)
• Autor: Písařík Marek (XPISM00)
• Typ modelu: Monte Carlo
• Modelovací nástroj: MS Office Excel 2010

Definice problému

Kasinovou hru ruleta je možné hrát náhodně, dle oblíbených čísel, intuice, či pomocí systematického vsázení. Existují 2 typy rulet. Francouzská (čísla 1-36 + neutrální políčko 0), či Americká ruleta (čísla 1-36 + 2x neutrální políčka 0 a 00). Matematickou výhodu rulety tvoří právě neutrální políčka, proto je vhodné si vždy zvolit pro hraní první typ. V každém kole vhodí krupiér kuličku v opačném směru, než je otáčení rulety. Hráči mohou vsázet na nespočet možností, jak dané kolo dopadne.

Možné sázky:

• číslo (popř. dvojice/čtveřice sousedících čísel)
• řada (popř. dvojice sousedících řad)
• sloupec
• tucty
• barva (červená/černá)
• sudá/lichá
• 1-18/19-36

Ve své simulaci se zaměřím na problematiku systematického sázení zejména na možnosti s 50% pravděpodobností (vyjma nuly) tedy červená/černá, sudost/lichost atd. Na tyto možnosti lze sázet dle matematických posloupností. U tohoto typu hraní je nezbytné disponovat dostatečně vysokým rozpočtem, který pokryje i málo pravděpodobnou řadu stejných hodnot.

Systémy:

• Martingale systém: vybereme si barvu a neustále na ní sázíme dvojnásobné částky, dokud daná barva nepadne, až ano. Poté budeme +1 násobené hodnoty (řada: 1,2,4,8,16,...)
• D‘ Alembert systém: funguje na stejném principu jako předchozí, jen při padnutí naší barvy nezačínáme od 1násobku hodnoty, nýbrž pouze o jednu hodnotu níže (tedy v případě že vyhrajeme v situaci, kdy sázíme 16ti násobek další kolo nesázíme 1násobek, ale 8mi násobek)
• Fibonacciho systém: Opět se jedná o systém podobný výše uvedeným, nicméně se vsází dle Fibonacciho posloupnosti, tedy vždy součet

Cíl simulace

V práci tedy budu simulovat náhodnost rulety, přičemž budu aplikovat všechny 3 systémy sázení. Vstupem do systému bude rozpočet, který na hru mám. A tedy v případě, že přijde smolně dlouhá série, na kterou rozpočet nebude stačit, hra končí a uživatel přišel o všechny peníze. Výsledkem bude dosažená částka na konci cyklu a tedy zhodnocení všech variant. Cílem simulace je tedy zhodnocení, který systém je nejvhodnější pro zadaný rozpočet. Nejvhodnějším se rozumí, při kterém dosáhnu s největší pravděpodobností nejvyšší výhry (pokud vůbec nějaké). posledních dvou hodnot posloupnosti (řada: 1,1,2,3,5,8,13,21,...)

Metoda

Jako nejvhodnější metodou pro řešení tohoto problému je právě metoda Monte Carlo. Důvod vhodnosti vychází z podstaty této metody a tedy z generování pseudonáhodných čísel, což přesně kopíruje realitu, kterou se snažíme simulovat. Generování čísel nahrazuje vhozenou kuličku do prostoru točící se rulety. Druhou možností, jak se dobrat k výsledku zkoumání je využít některé online kasino, ve kterém se dá nanečisto vyzkoušet hraní rulety bez nutnosti vložit peníze. Tento způsob je nicméně časově velmi náročný a proto byla zvolena metoda Monte Carlo v prostředí MS Office Excel 2010.

Model

Model zachycuje dění na ruletě, tedy generuje pro každé „kolo“ pseudonáhodnou hodnotu v intervalu <0;36>, která reprezentuje políčko, do kterého padne kulička. Tyto hodnoty jsou následně využívány pro simulaci sázení dle 3 zvolených systémů, tedy Martingale, D‘ Alembert a Fibonacci. Všechny systémy se hrají na stále stejnou zvolenou variantu s 50% procentní pravděpodobností výhry (vyjma nuly), v případě naší simulaci se jedná o sázky na sudost padnuté hodnoty. Každý ze systémů má svůj vlastní sloupec s vypočtenými hodnotami. Pro každou metodu nás zajímá:

• Kolik dané kolo vsázíme na námi vybranou barvu/sudost…
• Kolik jsme dané kolo vyhráli (pokud vůbec)
• Jaký je náš celkový stav konta po odehraném kole
• Jaký je náš stav konta po provedení sázky (tedy jestli máme ještě rozpočet na provedení sázky)

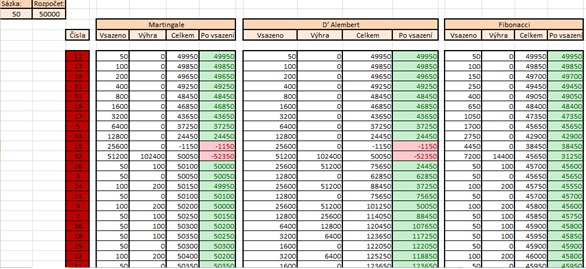
Následující obrázek zachycuje simulaci jednoho cyklu:

Nejdůležitější částí simulace je výpočet výšky sázky pro aktuální kolo:

Martingale systém

Jedná se o jednoduchý systém, při kterém se v případě prohry zdvojnásobuje sázka. Takto se postupuje až do doby, kdy padne námi zvolená hodnota. Jakmile se tak stane, začíná se vsázet od počáteční částky.

=KDYŽ(Minulé_číslo=0;Minulá_sázka*2;KDYŽ(ISEVEN(Minulé_číslo);Počáteční_částka;Minulá_sázka*2))

Testujeme nejprve nenulovost předchozího tahu. V případě, že byl nulový, aktuální sázka bude dvojnásobek sázky minulého kola. Pokud byl minulý tah nenulový, proběhne test sudosti. Pokud tažené číslo v minulém kole bylo sudé, vyhráli jsme a v aktuálním kole proběhne základní sázka, v opačném případě z důvodu lichosti zdvojnásobujeme sázku minulého kola.

Následné výpočty už jsou triviální. V poli výhra pouze testujeme sudost vygenerovaného čísla + nenulovost. Na základě těchto testů je výhra buď 0, nebo dvojnásobek vsazené částky. V kolonce celkem proběhne součet stavu konta po minulé sázce s rozdílem výhry a sázky aktuálního kola.

D‘ Alembert systém

V tomto případě pouze trochu modifikujeme předchozí systém. Rozdílnost vyplývá z chování hráče v případě výhry po delší neúspěšné sérii. V takovéto situaci nezačínáme vsázet od základní hodnoty, nýbrž se v posloupnosti posuneme pouze o jeden krok zpět. Výpočet sázky probíhá dle následujícího vzorce.

=KDYŽ(Minulé_číslo=0;Minulá_sázka*2;KDYŽ(ISEVEN(Minulé_číslo);KDYŽ(Minulá_sázka>Základní_sázka;Minulá_sázka/2;Základní_sázka);Minulá_sázka*2))

Výpočet probíhá velmi podobně jako v předchozím případě. Výjimkou je vnořená podmínka testující velikost minulé sázky. Pokud je větší než počáteční sázka, dělíme ji 2, v opačném případě bude tvořit výši aktuální sázky hodnota té počáteční.

Ostatní výpočty jsou stejné jako v předchozím případě.

Fibonacciho systém Sázení dle Fibonacciho posloupnosti si vyžádá nejsložitější vzorec pro výpočet aktuální sázky

=KDYŽ(Minulé_číslo =0;KDYŽ(Minulá_sázka=Základní_sázka;2* Základní_sázka; Minulá_sázka +Předminulá_sázka);KDYŽ(ISEVEN(Minulé_číslo); Základní_sázka;KDYŽ(Minulá_sázka = Základní_sázka;2* Základní_sázka; Minulá_sázka + Předminulá_sázka)))

Nejprve opět testujeme nulovost minulého generovaného čísla. V případě prohry, tedy nulovosti, zjišťujeme velikost minulé sázky. Pokud byla ve výši základní sázky, zdvojnásobíme ji, v opačném případě proběhne určení hodnoty aktuální sázky součtem sázek v posledních dvou kolech. Když generované číslo bude nenulové, proběhne obdobný vnořený proces určování výše aktuální sázky. Ostatní výpočty jsou opět stejné jako v předchozích případech.

Výpočet vyhodnocení pro daný cyklus:

Pro zjištění výsledků daného cyklu generování čísel při jednotlivých systémech probíhá následujícím způsobem. Pro každé kolo generování čísel se v sloupci „Po sázce“ zaznamenává hodnota stavu našeho konta po provedení sázky. Na konci cyklu zjistíme funkcí MIN nejnižší hodnotu, které tento sloupec nabyl. Pokud nalezneme údaj v mínusové hodnotě, cyklus jsme prohrály a stav po tomto cyklu je Rozpočet*(-1). V opačném případě jsme byli úspěšní a výši výhry získáme rozdílem Stavu konta po posledním kole a rozpočtu.

Výsledky

Simulace byla provedena v 300.000 provedeních, rozdělených dle různých vstupních kritérií. Jako vstupní data, byly použity pro každý systém poměry mezi základní částkou a rozpočtem a to v hodnotě 10, 50, 100 a 500 násobky základní sázky. Tyto poměry byly aplikovány na počty odehraných kol v intervalu 50 až 1000. Pro všechny tyto kombinace byla provedena simulace 1000x a výsledky byly zprůměrovány. V níže uvedených grafech jsou graficky znázorněny dosažené hodnoty. Z grafů lze vyčíst vliv měnění výše poměru základní sázky/rozpočtu vůči počtu odehraných kol.

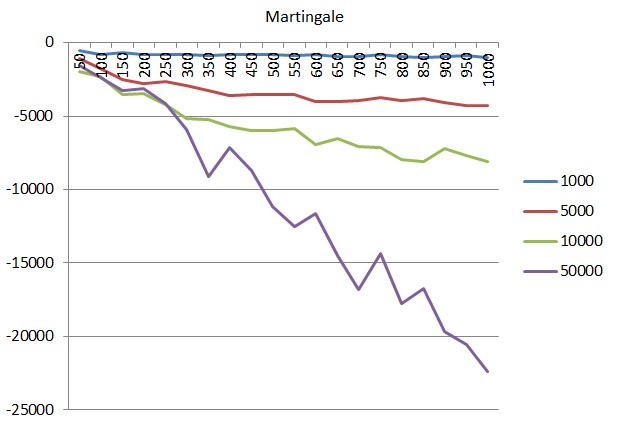
Martingale systém

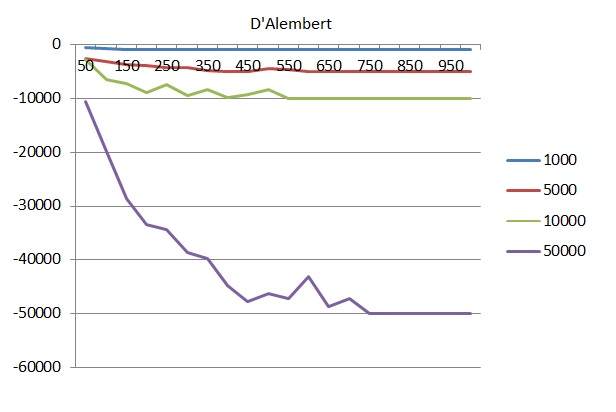
D’Alambert systém

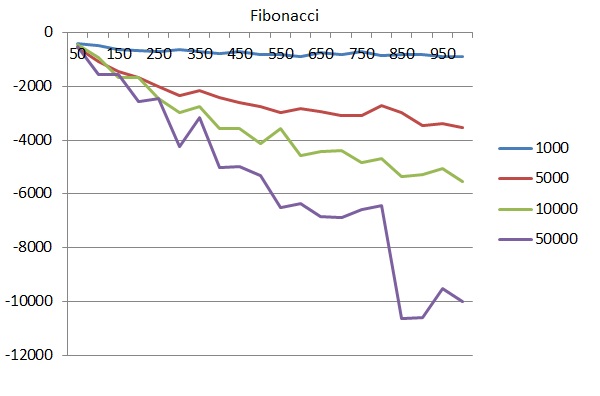
Fibonacci systém

Z výše uvedených hodnot lze vyčíst základní odpověď a to, že systémové hraní rulety z dlouhodobého hlediska nepřináší zisk. Všechny provedené kombinace po celkovém zprůměrování vykazují ztrátové hodnoty. Další tendence, které lze z grafů zjistil lze interpretovat jako. Čím vyšší rozpočet, tím vyšší dosažené ztráty. A současně. Čím více odehraných kol v jednom cyklu, tím rovněž vyšší ztráty.

Závěr

Podařilo se mi věrohodně nasimulovat průběh hry ruleta, včetně systémového vsázení. Výsledky potvrdily matematickou výhodu na straně kasina díky existenci neutrálního políčka nula. Omezením mé simulace může být jev, že se provozovatelé kasin brání systémovému hraní pomocí maximální sázky, čímž hráče limitují. Druhým způsobem obrany proti tomuto typu hraní je možnost vykázání takovéhoto hráči pomocí hlídačů, kteří takovéto hráče upozorní velmi nešetrný způsobem, že u nich se systémovým způsobem hrát nesmí. Existuje ale i internetová alternativa hraní rulety, kde takováto omezení nejsou.

Kód

File:Simulace ruleta.xlsx