Difference between revisions of "Pension System Czech Republic"
(Created page with "=Introduction= Simulation of pension reform in the Czech Republic: Analysis of long-term sustainability '''What will be simulated:''' A system dynamics model of the Czech...") |
(→Model) |
||
| Line 17: | Line 17: | ||
[[File:PensionReformModel.png]] | [[File:PensionReformModel.png]] | ||
| + | |||
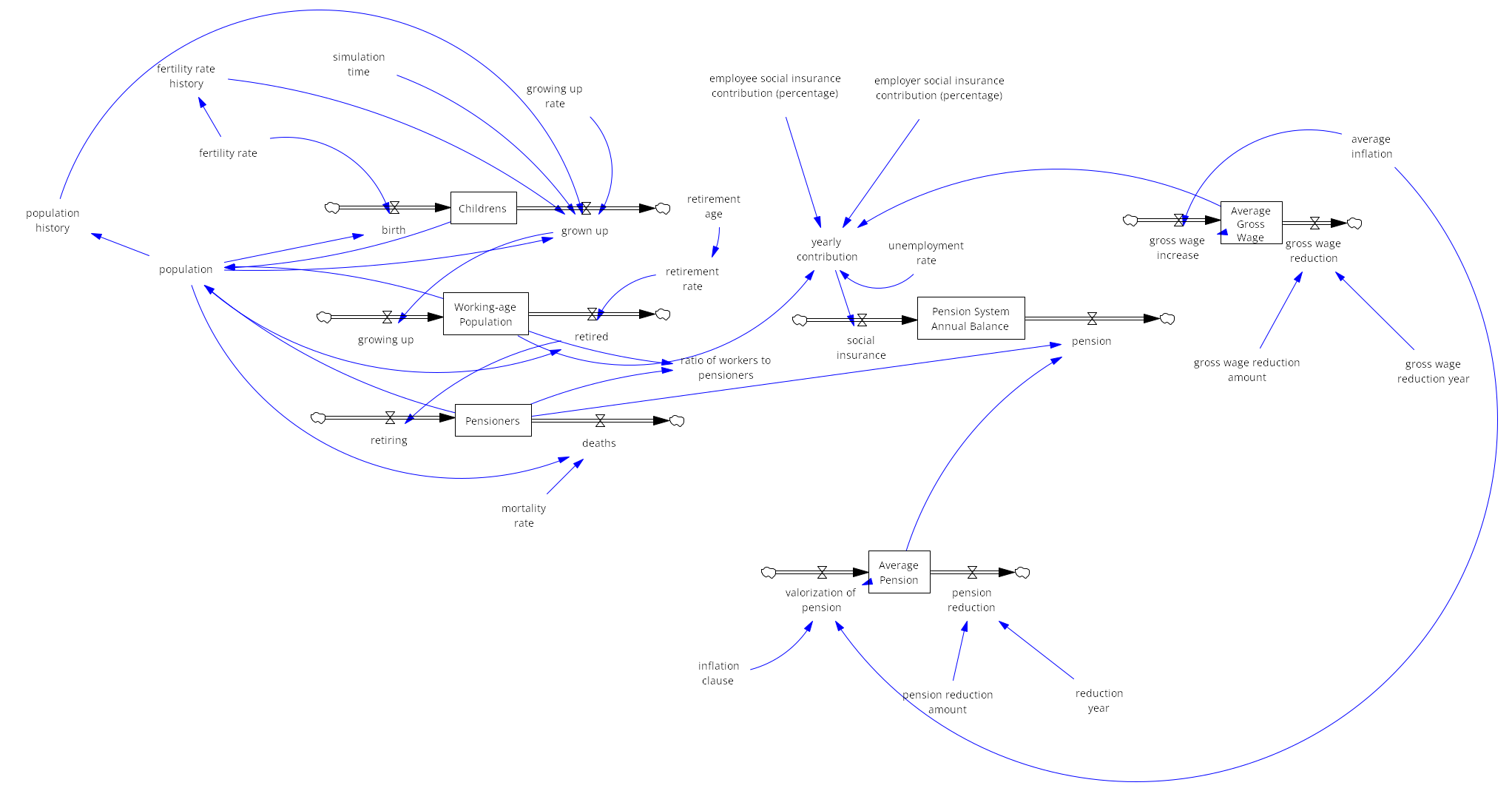
| + | The model represents the dynamics of the Czech pension system, divided into key components: population structure, contributions to the pension system, and pension expenditures. | ||
| + | |||
| + | '''Population structure''' | ||
| + | |||
| + | The population is categorized into children (ages 0–19), working-age population (ages 20–64), and pensioners (65+ years). Children grow up and transition into the working-age population, which contributes to the pension system through employment. Over time, individuals retire and become pensioners, withdrawing from the pension system. The retirement age determines the rate at which the working-age population transitions to retirement, with a higher retirement age reducing the retirement rate and vice versa. | ||
| + | |||
| + | |||
| + | '''Contribution to the pension system''' | ||
| + | |||
| + | The working-age population contributes to the system through social insurance contributions, based on the average gross wage. Contributions come from both employees and employers, while unemployment reduces the total contributions collected. The model assumes that the gross wage grows annually, at least partially indexed to inflation (e.g., one-third of the inflation rate). | ||
| + | |||
| + | '''Pension expenditures''' | ||
| + | |||
| + | Pensioners withdraw funds from the system based on the average pension, which is periodically adjusted through pension valorization. The inflation clause determines the extent to which pensions are indexed to inflation, ensuring their real value remains stable over time. | ||
| + | |||
| + | '''External adjustments''' | ||
| + | |||
| + | The model includes variables for one time reductions in both the average gross wage and the average pension in a specific year. These adjustments simulate policy interventions (e.g., government mandated pension reductions) or external shocks (e.g., an economic crisis) that impact wages or pensions. | ||
| + | |||
| + | This dynamic interaction between population groups, contribution flows, and pension expenditures allows for the simulation of various policy scenarios, illustrating the long-term sustainability of the pension system. | ||
| + | |||
=Results= | =Results= | ||
Revision as of 13:22, 8 January 2025
Introduction
Simulation of pension reform in the Czech Republic: Analysis of long-term sustainability
What will be simulated:
A system dynamics model of the Czech pension system that simulates the long-term financial sustainability under varying demographic, economic, and policy scenarios. The simulation will project future balances of the pension system, incorporating the flows of revenues (social insurance contributions) and expenditures (pension payouts)
Problem definition
The main goal is to analyze how different pension reform strategies (e.g., adjusting retirement age, altering contribution rates, changing the indexation formula of pensions) will affect the long-term stability of the Czech pension system. The simulation aims to identify specific policy levers and thresholds that ensure the pension system’s financial equilibrium over a multi-decade horizon, despite changing demographic and economic conditions.
Method
The System Dynamics method was chosen for its ability to model complex systems with multiple influencing variables, inflows, and outflows. Alternative approaches, such as Monte Carlo analysis or agent-based modeling in NetLogo, were deemed unsuitable for this case as they cannot adequately capture the dynamic interactions and feedback loops between demographic, economic, and policy variables. Vensim PLE was selected as the simulation environment due to its accessibility and support for this type of modeling.
Model
The model represents the dynamics of the Czech pension system, divided into key components: population structure, contributions to the pension system, and pension expenditures.
Population structure
The population is categorized into children (ages 0–19), working-age population (ages 20–64), and pensioners (65+ years). Children grow up and transition into the working-age population, which contributes to the pension system through employment. Over time, individuals retire and become pensioners, withdrawing from the pension system. The retirement age determines the rate at which the working-age population transitions to retirement, with a higher retirement age reducing the retirement rate and vice versa.
Contribution to the pension system
The working-age population contributes to the system through social insurance contributions, based on the average gross wage. Contributions come from both employees and employers, while unemployment reduces the total contributions collected. The model assumes that the gross wage grows annually, at least partially indexed to inflation (e.g., one-third of the inflation rate).
Pension expenditures
Pensioners withdraw funds from the system based on the average pension, which is periodically adjusted through pension valorization. The inflation clause determines the extent to which pensions are indexed to inflation, ensuring their real value remains stable over time.
External adjustments
The model includes variables for one time reductions in both the average gross wage and the average pension in a specific year. These adjustments simulate policy interventions (e.g., government mandated pension reductions) or external shocks (e.g., an economic crisis) that impact wages or pensions.
This dynamic interaction between population groups, contribution flows, and pension expenditures allows for the simulation of various policy scenarios, illustrating the long-term sustainability of the pension system.