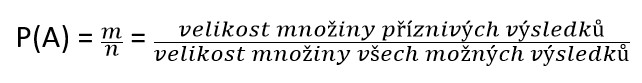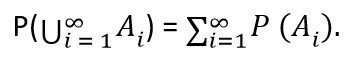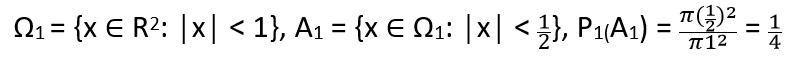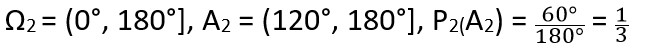Uniform distribution

Úvod

V běžném životě se setkáváme s procesy, u kterých není snadné předem určit, jak dopadnou. Pokud se tento problém převede do světa matematiky, tak se jedná o jevy, u kterých nejsme schopni předem s jistotou určit, jaký z možných výsledků nastane. Takto predikovat výsledek není často možné z důvodu, že je sledovaný jev příliš složitý a komplexní, nebo o něm nejsou známy všechny potřebné informace, tj. jeho výsledek je určen nějakou náhodou. Pro lepší představu je možné si pod těmito jevy představit různé experimenty, testy, přírodní jevy apod.

Touto problematikou se zabývá teorie pravděpodobnosti. Ta se snaží tuto náhodu určit matematicky. Výsledkům pokusů přiřazuje jejich pravděpodobnost, která udává podíl případů, kdy nastane daný výsledek. Na základě těchto jednoduchých modelů je pak možné řešit složitější problémy.

Například: Máme k dispozici vyváženou (nebo také spravedlivou) minci. Za pomoci této mince můžeme spočítat, jaká je pravděpodobnost, že nám z 2000 hodů padne 100 orlů. Zde je důležité specifikovat, že se jedná o vyváženou (nebo také spravedlivou) minci. Kdyby nebyla mince vyvážená, padala by panna nebo orel častěji a tento experiment by tím byl značně zkreslen.

Termilonogie

Veškeré popsané definice by měly být popsány v kapitole Opáčko ze statistiky: Pravděpodobností rozdělení nebo Pravděpodobnostní rozdělení. Jelikož je opakování matka moudrosti, budou zde v krátkosti popsány základní definice z teorie pravděpodobnosti, které nejsou stoprocentně pokryty ve výše zmíněných kapitolách.

Experiment, pravděpodobnostní prostor a náhodný jev

Na začátku je třeba matematicky definovat, co znamená jev a experiment. Jev je možné popsat jako množinu, které se bude přiřazovat pravděpodobnost. Experiment je poté definován jako pravděpodobnostní prostor, který je určen jako trojice:

ε = (Ω, Ϝ, Ρ),

kde Ω obsahuje všechny výsledky určitého experimentu, Ϝ označuje kolekci všech možných jevů, kterým je možné přiřadit pravděpodobnost P.

Náhodný jev A je možné chápat jako množinu elementárních jevů, tedy nějakou podmnožinu A z množiny Ω.

Například: Hod dvěma vyváženými mincemi – množinově vyjádřený jev, že padne alespoň jednou panna P (orel značen O). Prostor elementárních jevů je Ω = {(P, P), (P, O), (O, P), (O, O)}. Sledovaný jev A tedy bude: A = {(P, P), (P, O), (O, P)} tj. podmnožina množiny Ω.

Takto množinově definovaný jev je velmi užitečný, protože je poté možné používat množinové operace jako je sjednocení a průnik dvou a více množin nebo opačný jev k jevu A.

Klasická definice pravděpodobnosti

Za klasickou definici pravděpodobnosti je možné považovat tu, kterou zformoval francouzský matematik Pierre-Simon Laplace na přelomu 18. století a je definována takto:

P(A) značí pravděpodobnost sledovaného jevu A (například zmíněný hod mincí), která je rovna podílu příznivých výsledků a všech možných výsledků. Definice předpokládá, že se jedná o konečný počet výsledků několika vzájemně různých pokusů, které jsou všechny stejně pravděpodobné (viz poznámka o vyvážené minci).

Například: Pozorovaný jev A je hod vyváženou mincí. Zajímá mě, jaká je pravděpodobnost, že padne orel. Mince má dvě strany, na jedné panna a na druhé orel. Všechny možné výsledky jsou 2 a mě zajímá pouze orel. Výsledkem je tedy 0,5, tj. 50% šance, že padne orel.

Jelikož je možné vyjádřit pravděpodobnost procenty, je její hodnota v rozmezí mezi 0 % a 100 %, to jest výsledek podílu výše je mezi 0 a 1 a současně platí, že je maximálně 1. Toto vychází z definice pravděpodobností míry (viz kapitola níže). Toto je možné jednoduše vysvětlit na příkladu s vyváženou mincí.

Pravděpodobnost, že padne orel, je stejná jako, že padne panna. Toto jsou jediné dva výsledky, které mohou nastat. Pokud sečtu pravděpodobnosti všech možných výsledků, dostanu hodnotu 1 (0,5 + 0,5 = 1).

Vedle této klasické definice pravděpodobnosti, je možné v jiných textech nalézt jiné definice (například dle A. N. Kolmogorova, axiomatickou, statistickou či geometrickou). Pro jednodušší vysvětlení rovnoměrného rozdělení je zde uvedena ještě jedna definice a to grafická.

Grafická definice pravděpodobnosti

Grafická definice pravděpodobnosti nahlíží na sledovaný jev A z hlediska jeho relativní velikosti. Předpokládá, že výsledky tohoto jevu nastávají v nějakém geometrickém objektu či množině o konečné velikosti (například plochy, délky, objemu apod.), kde je každý tento výsledek (například bod) stejně pravděpodobný. Pravděpodobnost tohoto jevu A je poté definována takto:

Stejně jako je napsáno u klasické definice pravděpodobnosti, je analogicky odůvodnitelné, že součet pravděpodobností všech výsledků je 1, tj. maximální velikost množiny (plochy) je 1.

Například: Romeo a Julie se mají setkat na tajném místě mezi polednem a 1 hodinou odpoledne. Každý z nich dorazí v náhodném okamžiku v tomto určeném čase a počká zde pouze 15 minut. Pokud ten druhý nedorazí, odejde. Jaká je pravděpodobnost, že se potkají.

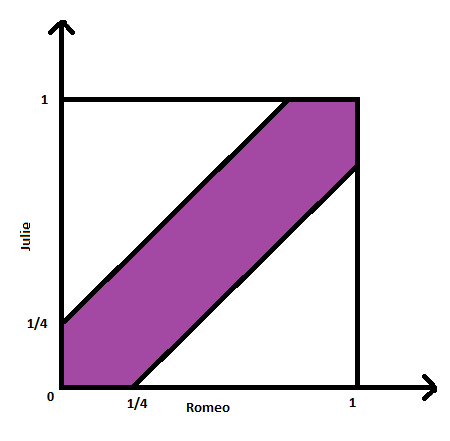
Celková plocha je 1. Vybarvená oblast odpovídá situacím, kdy se setkají. Pravděpodobnost, že se potkají je následující:

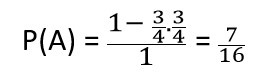
Pro určení výsledku byla použita pravděpodobnost opačného jevu a nezávislosti dvou pozorovaných jevů.

Pravděpodobnostní míra

Pravděpodobnostní míra na (Ω, Ϝ) je funkce P: F → R (F je zobrazení na množinu reálných čísel) splňující:

    1) nezápornost: pro každé A ∈ F platí P(A) ≥ 0,

    2) normalizace: P(Ω) = 1,

    3) σ – aditivita: když jsou A₁, A₂ … ∈ F vzájemně disjunktní jevy (A_i ∩ A_j = ∅ pro ∀i, j: i ≠ j), tak

 

Z této definice plyne, že pro každé A ∈ F platí 0 ≤ P(A) ≤ 1. Jak již bylo zmíněno výše, pravděpodobnost je možné uvádět v procentech tj. 0 % až 100 %. Je nutné správně definovat volbu P a to, co je myšleno pod pojmem „náhodný“. Vágně zadaný příklad může vést k paradoxům.

Například: Bertrandův paradox – Náhodná tětiva X na jednotkové kružnici. Jaká je pravděpodobnost P(A), kde A = {│x│ > l} a l je strana libovolného vepsaného rovnostranného trojúhelníku? Zde záleží na tom, co je míněno pod slovem „náhodná“:

    1) Vybereme rovnoměrně náhodně střed x:

    2) Vybereme rovnoměrně náhodně úhlovou velikost a směr tětivy x viděné ze středu:

  

    3) Vybereme rovnoměrně náhodně vzdálenost tětivy x od středu a směr:

   

Náhodné veličiny

Výsledkem náhodného experimentu často nebývá číslo. Aby bylo možné takové experimenty matematicky zpracovat, je vhodné každému výsledku přiřadit jeho číselnou hodnotu. Vhodným přiřazením je výběr informace, která je pro nás zajímavá. Toto přiřazení je možné provést několika způsoby, proto je nazýváno náhodnou veličinou a značí se X, Y, apod.

Například: Počítání orlů při hodu vyváženou mincí: X(orel) = 1, X(panna) = 0. Toto přiřazení je vyobrazené na obrázku níže.

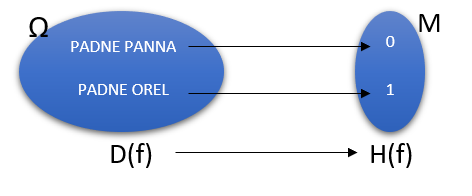
Matematicky je definice stanovená takto: Náhodná veličina X na pravděpodobnostním prostoru (Ω, F, P) je funkce, která každému výsledku experimentu ω ∈ Ω přiřadí hodnotu X(ω) ∈ R a pro kterou platí podmínka měřitelnosti:

{X ≤ x} ∈ F pro všechna x ∈ R.

Podmínka měřitelnosti říká, že {X ≤ x} je náhodný jev, u kterého je možní spočítat jeho pravděpodobnost.