Difference between revisions of "User:Bacj04"
| Line 45: | Line 45: | ||
= Detailný popis modelu = | = Detailný popis modelu = | ||
| − | ( | + | [[File:bacj04_model.png|thumb|550px|right|Ukážka vytvoreného modelu]] Ako je možné vidieť i na obrázku vedľa, prostredie modelu je zložené z nasledujúcich hlavných prvkov: |
| − | + | * '''Mapa''', ktorá má veľkosť 33x33 zelených dlaždíc (''patches''), neprechodné okraje (ak sa ktorýkoľvek zberač vydá dole, nemôže sa objaviť hore), päť osôb s rôznymi farbami reprezentujúcimi jednotlivých zberačov, a užívateľom zadaný počet červených kruhov znázorňujúcich jahody a stromov zohrávajúcich rolu prekážok s danou veľkosťou | |
| − | + | * '''Tlačidlá''' s názvami ''Setup'' a ''Run'', prostredníctvom ktorých je možné pripraviť prostredie mapy na simuláciu a spustiť ju (prípadne ju i pozastaviť) | |
| − | + | * '''Posuvníky''', ktorých nastavením je možné meniť jednotlivé parametre modelu (počet jahôd, počet stromov, veľkosť stromov, rýchlosť pohybu zberačov) | |
| − | ( | + | * '''Monitory''' zobrazujúce aktuálny počet jahôd, ktoré jednotliví zberači odlíšení farbami doposiaľ získali |
=== Agenty modelu === | === Agenty modelu === | ||
| − | (...) | + | Pre pochopenie funkcionality vytvoreného modelu sa stačí zamerať na takzvané korytnačky (''turtles''). Hoci by sa na prvý pohľad mohlo zdať, že nimi sú iba jednotliví zberači, pravdou je, že sa ich v modeli vyskytuje viac. Sú to konkrétne: |
| + | * '''trees:''' Ako to už vyplýva i z názvu, sú to práve prekážky pomenované ako stromy, ktorých jedinými kľúčovými vlastnosťami okrem ich vzhľadu sú súradnice, na ktorých sa nachádzajú, a ich veľkosť. Pri príprave prostredia mapy sú náhodne rozmiestnené tak, aby sa vzájomne neprekrývali, pričom v prípade, že s nimi počas simulácie prídu zberači do kontaktu, tak nemôžu ísť ďalej bez toho, aby ich oblúkom obišli. | ||
| + | * '''strawberries:''' Tieto korytnačky reprezentujú jahody, ktorých získanie je hlavným cieľom všetkých zberačov. Okrem vizuálnych vlastností majú iba súradnice, ktoré udávajú, kde sa vyskytujú, a informáciu o tom, či po nich aktuálne ide nejaký zo zberačov. Pri príprave prostredia mapy sú takisto náhodne rozmiestnené, a to tak, aby sa neprekrývali navzájom, no zároveň aby neboli na nejakom mieste, kde by sa k ním nedalo dostať (napríklad v korunách stromov). V prípade, že prídu do kontaktu so zberačmi, zomrú (zmiznú z mapy) a pripočítajú sa k ich aktuálnemu zisku. | ||
| + | * '''people:''' Takzvaní ľudia reprezentujú jednotlivých spomínaných zberačov. Okrem vizuálnych vlastností obsahujú opäť súradnice, no zároveň aj informáciu o tom, po akej jahode aktuálne idú, do akej strany sa vyhnú v prípade kolízie s prekážkou a koľko už nazbierali jahôd. Ich identita (a tým pádom do istej miery i chovanie) je daná farbou, pričom na začiatku sú tiež náhodne rozmiestnení tak, aby sa neprekrývali navzájom a aby sa nedotýkali žiadnej jahody či stromu. Od samého počiatku simulácie si postupne vždy na základe ich stratégie vyberajú nejakú jahodu, za ktorou sa vydajú až do doby, než ju získajú alebo im ju niekto ukradne. Musia sa však i vyhýbať stromom, čo všetci dosahujú tým, že ako náhle s nejakým prídu do kontaktu, tak sa oblúkom vyberú buď doprava alebo doľava, kým nemajú zasa voľnú cestu (keby sa náhodou niekde zasekli, tak jednoducho zmenia smer). | ||
=== Parametre a obory hodnôt modelu === | === Parametre a obory hodnôt modelu === | ||
| − | + | V aktuálnej verzii modelu je možné bez zasahovania do zdrojového kódu nastavovať nasledujúce parametre, ktoré sú definované i v zadaní: | |
| + | * '''number-of-trees:''' Tento celočíselný parameter udáva počet stromov. Minimálna hodnota, ktorú môže naberať, je 1, pričom maximálna hodnota je 60, keďže pri najväčšej možnej veľkosti prekážok by nebolo možné pripraviť prechodnú mapu s vyšším počtom. | ||
| + | * '''number-of-strawberries''' Tento celočíselný parameter udáva počet jahôd. Minimálna hodnota, ktorú môže naberať, je takisto 1, pričom maximálna hodnota je tentokrát až 500, čo je vzhľadom na veľkosť mapy podľa názoru autora práce viac než dosť. | ||
| + | * '''scale-of-trees:''' Na rozdiel od ostatných parametrov má tento, ktorý udáva veľkosť stromov, povolené iba hodnoty 1.0, 1.5, 2.0, 2.5 a 3.0. Dôvod je skrátka ten, že pri menšej veľkosti by prekážky nepredstavovali žiadny problém pre zberačov, pričom pri väčšej by naopak obzvlášť u maximálneho možného počtu pokrývali väčšinu mapy, čo by ju činilo neprechodnou. | ||
| + | * '''movement-speed:''' Tento celočíselný parameter rozhoduje o rýchlosti pohybu zberačov. Minimálna hodnota, ktorú môže naberať, je 1, pričom maximálna hodnota je 100, keďže pri väčšej rýchlosti by už ich prakticky ani nebolo možné efektívne sledovať. | ||
=== Metódy modelu === | === Metódy modelu === | ||
| − | (...) | + | Zdrojový kód modelu pozostáva z niekoľkých metód, pričom každá jedna z nich plní nejakú zásadnú funkciu. Jedná sa konkrétne o: |
| + | * '''setup:''' V tejto metóde sa pripravuje všetko v rámci prostredia mapy a lokálnych i globálnych premenných, čo je potrebné na realizáciu simulácie (viď metódy nižšie). | ||
| + | ** '''set-globals:''' Táto metóda definuje identity zberačov prostredníctvom čísla vyjadrujúceho nejakú farbu a počiatočné nulové hodnoty jahôd nachádzajúcich sa v jednotlivých kvadrantoch mapy. | ||
| + | ** '''setup-grass:''' V tejto metóde sa akurát nastaví farba dostupných dlaždíc na zelenú. | ||
| + | ** '''setup-trees:''' Táto metóda je využívaná na vytvorenie náhodne rozmiestnených korytnačiek reprezentujúcich stromy (viď ''trees'' vyššie pre viac informácií). | ||
| + | ** '''setup-strawberries:''' V tejto metóde sú vytvorené náhodne rozmiestnené korytnačky reprezentujúce jahody (viď ''strawberries'' vyššie pre viac informácií). | ||
| + | ** '''setup-people:''' Táto metóda vytvorí náhodne rozmiestné korytnačky reprezentujúce zberačov (viď ''people'' vyššie pre viac informácií). | ||
| + | *** '''get-random-coordinates:''' Táto metóda je využívaná v rámci viacerých vyššie zmieňovaných metód na nastavenie náhodných súradníc. | ||
| + | *** '''count-strawberries:''' Táto metóda slúži na úvodné popočítanie jahôd vyskytujúcich sa v jednotlivých kvadrantoch mapy. | ||
| + | *** '''get-identity:''' Táto metóda akurát priradí vytvoreným zberačom jednotlivé vopred definované identity prostredníctvom farieb. | ||
| + | * '''go:''' Táto metoda zabezpečuje priebeh simulácie po príprave prostredia až do doby, než sú pozbierané úplne všetky jahody. | ||
| + | ** '''choose-target:''' V tejto metóde je definovaný spôsob výberu nadchádzajúcej jahody jednotlivými zberačmi na základe ich identity (podrobnejší popis ich stratégií sa nachádza v definícii problému). | ||
| + | ** '''move-to-target:''' Táto metóda popisuje pohyb jednotlivých zberačov a očakávané chovanie korytnačiek v prípade, že osoby prídu do kontaktu s nejakou prekážkou alebo jahodou. | ||
=== Obmedzenia modelu === | === Obmedzenia modelu === | ||
| − | (... | + | Ako bolo spomenuté už vyššie, jedným z primárnych obmedzení vytvoreného modelu je nastaviteľnosť parametrov. Vzhľadom na veľkosť mapy totiž nie je možné prekročiť určité hodnoty, inak by sa stala neprechodnou a tým pádom by simulácia nemohla byť uskutočnená. V možnostiach rozšírení zadania sa navyše uvádza i možnosť doplnenia ďalších parametrov (ako napríklad miera únavnosti, na základe ktorej sa všetci zberači postupne budú spomaľovať až pokiaľ nezastanú úplne za účelom krátkeho oddychu), ktoré by mohlo byť zaujímavé implementovať, no pre časové nároky a potreby predmetu museli byť vynechané. |
| + | |||
| + | Ďalším obmedzením je inteligencia samotných zberačov. Hoci sa totiž dokážu úspešne vyhýbať prekážkam, nie sú v aktuálnej verzii schopní určiť, či sa im je výhodnejšie vyhnúť zľava alebo sprava, alebo či by nebolo lepšie v prípade, že im v ceste stojí veľa stromov za sebou, vydať trochu inou cestou. Podľa názoru autora by však vzhľadom na to, že po tejto stránke sú na tom všetci zberači rovnako, táto skutočnosť nemala mať v konečnom dôsledku zásadný vplyv na získané výsledky simulácií. | ||
= Výsledky = | = Výsledky = | ||
| − | (.. | + | Pred zahájením simulácie bol model v prvom rade riadne otestovaný autorom práce s rôznymi parametrami pri minimálnej rýchlosti zberačov, aby bolo možné jednoznačne overiť, že sa chovajú presne podľa očakávaní. Následne bol už prevedený samotný prieskum, a to vždy s využitím výsledkov piatich simulácií pre štyri najpodstatnejšie kombinácie parametrov (vzhľadom na to, že rýchlosť pohybu má rovnaký vplyv na všetkých zberačov, nastavenie tohto parametru možno podľa názoru autora v rámci dosiahnutia čo najpestrejších výsledkov zanedbať). Výsledky (počet jahôd, ktorý jednotlivé osoby nazbierali) je možné vidieť v nasledujúcich prehľadných tabuľkách: |
| + | |||
| + | [[File:bacj04_results.png|660px]] | ||
=== Adamova stratégia === | === Adamova stratégia === | ||
| − | + | Niet divu, že zo všetkých zberačov dopadol Adam jednoznačne najhoršie. Stratégia kompletne náhodného výberu jahôd pravidelne obsadzuje '''posledné a predposledné miesto''', pričom iba málokedy sa jej podarí umiestniť vyššie. Nie je zároveň asi ani nijak zvlášť prekvapivé, že najväčšiemu úspechu sa Adam teší pri nižšom počte jahôd, keďže v takom prípade často záleží viac na dobrej štartovnej pozícii ako na inteligencii korytnačky. Na samotných prekážkach naopak nijak zvlášť nezáleží, pričom jednoznačne najlepšie výsledky bude Adam logicky vykazovať s jednou jedinou dostupnou jahodou a najhoršie s maximálnym počtom jahôd. Rozhodne sa teda nejedná o optimálnu stratégiu výberu. | |
=== Bohumilova stratégia === | === Bohumilova stratégia === | ||
| − | + | Bohumil je v porovnaní s Adamom už na prvý pohľad výrazne šikovnejším zberačom. Hoci je totiž jeho stratégia výberu veľmi jednoduchá, keďže spočíva čisto len v posúdení, ktorá jahoda sa pri ňom aktuálne nachádza najbližšie, teší sa pravidelnému úspechu a takmer garantovanému '''druhému miestu'''. Opäť asi nie je veľmi prekvapivé, že pri nižšom počte jahôd má o čosi horšie výsledky, keďže v takom prípade viac záleží na štartovnej pozícii a rozmiestnení prekážok. Čím viac jahôd sa však vyskytuje na mape, tým sú jeho výsledky lepšie. Jednoznačne najlepšie na tom každopádne Bohumil bol pri vysokom počte jahôd a vysokom počte menších prekážok. Jeho stratégia teda patrí medzi tie najoptimálnejšie. | |
=== Cyrilova stratégia === | === Cyrilova stratégia === | ||
| − | (... | + | Najväčším prekvapením pre autora práce boli Cyrilove výsledky. Hoci má totiž potenciálne najkomplexnejšiu stratégiu, keďže si musí najskôr vybrať, do ktorého kvadrantu sa najviac oplatí ísť, najčastejšie okupoval až '''tretie miesto''' a pri nižšom počte jahôd sa pravidelne umiestňoval i nižšie (dvakrát dokonca na poslednom mieste). Pri nižšom počte jahôd a vysokom počte veľkých prekážok mala Cyrilova stratégia najmenej konzistentný úspech, pričom naopak pri vysokom počte jahôd sa bez ohľadu na počet a veľkosť prekážok najviac stabilizovala. Dôvod je s najvyššou pravdepodobnosťou skrátka ten, že je až príliš závislá na hustote jahôd (pokiaľ sú rozmiestnené približne rovnomerne, tak dáva väčší zmysel od samého začiatku ísť po jahodách, ktoré sa pri zberačovi nachádzajú najbližšie) a konaní konkurentov (často sa totiž stávalo, že než sa Cyril dostal na to takzvané najvýhodnejšie miesto, predbehli ho jeho súperi). Táto stratégia teda patrí medzi optimálnejšie skôr v prostredí, ktoré nie je kompetitívne. |
=== Denisova stratégia === | === Denisova stratégia === | ||
| − | + | Denisova stratégia sa s tou Adamovou najčastejšie delila o '''posledné a predposledné miesto'''. Hoci totiž na prvý pohľad dáva zmysel spoliehať sa na rozhodnutia konkurencie a snažiť sa ju predbehnúť, keďže sa Denis stavia do neustáleho súboja o to, či sa k svojmu cieľu dostane skôr ako vybraný konkurent, je logické, že i najviac riskuje. Žiadne z nastaviteľných parametrov nemali nijak zvlášť veľký vplyv na úspech tohto zberača. Najlepšie sa mu bude dariť, keď si zhodou okolností vyberie toho najúspešnejšieho konkurenta, no i tak sa s najvyššou pravdepodobnosťou podľa všetkého ani raz neumiestni na prvom či druhom mieste. Jedná sa teda nepochybne o jednu z najmenej optimálnych stratégií. | |
=== Erikova stratégia === | === Erikova stratégia === | ||
| − | + | Erik bol nepochybne jednoznačným víťazom takmer pri akejkoľvek kombinácii parametrov, ktorý skoro vždy obsadil '''prvé alebo druhé miesto'''. Nie nadarmo sa hovorí, že kde sa dvaja bijú, tretí vyhráva. Skutočnosť, že totiž pri výbere vždy uprednostil jahodu, ktorá sa pri ňom nachádzala najbližšie a zároveň po nej nikto iný nešiel, mu zaručila, že sa k väčšine cieľov dostal ako prvý. Prekvapivo ale najlepšie výsledky vykazoval pri nižšom počte jahôd s nízkym počtom malých prekážok a vysokom počte jahôd s nízkym počtom veľkých prekážok, čo by mohlo znamenať, že na Erikovu úspešnosť mal najväčší vplyv práve spomínaný počet stromov. To však nič nemení na tom, že aj v ostatných prípadoch bol aspoň veľmi blízko prvému alebo druhému miestu, takže podľa názoru autora niet najmenších pochýb o tom, že sa vo vytvorenom modeli za akýchkoľvek okolností jedná o najkonzistentnejšiu a najoptimálnejšiu stratégiu. | |
| − | = | + | = Záver = |
| − | + | Primárnym cieľom tejto práce bolo porovnať päť rôznych prístupov k zberu surovín reprezentovaných jahodami v kompetitívnom prostredí. Zvoleným riešením bolo vytvorenie jednoduchého multiagentového modelu znázorňujúceho zber jahôd piatimi súperiacimi osobami v lese plnom prekážok s využitím nástroja NetLogo. Hoci je výsledný model výrazným zjednodušením reality, ktorý neberie do úvahy mnohé vnútorné či vonkajšie faktory, tento cieľ je podľa názoru autora možné považovať za splnený. S ohľadom na očakávané obmedzenia sa totiž podarilo získať pomerne veľa logických informácií, ako napríklad skutočnosť, že najväčší zmysel dáva vyberať si vždy tie najbližšie umiestnené suroviny, na ktoré sa ostatní nesústredia, pričom naopak najmenší úspech bude takmer určite mať čisto náhodný postup. | |
| − | |||
| − | |||
| − | (. | + | Na vytvorený model je možné nadviazať i v budúcnosti jeho rozšírením o ďalšie nastaviteľné parametre, viacero typov máp s rozdielnymi podmienkami, iné prekážky s rôznymi vlastnosťami alebo prípadne i ľubovoľné dodatočné stratégie, ktoré by taktiež mohlo byť zaujímavé porovnať. Zmysel by taktiež podľa názoru autora práce dávalo aj zdokonalenie spomínaného vyhýbania sa prekážkam a celkovej inteligencie agentov, aby mohli včas reagovať i na komplexnejšie situácie (napríklad v prípade, že by Denis zistil, že si vybral nešikovného súpera, tak by mohol sám od seba zmeniť svoj cieľ). |
= Referencie = | = Referencie = | ||
| Line 103: | Line 124: | ||
= Kód modelu = | = Kód modelu = | ||
| − | [[ | + | [[:File:Bacj04_proj.nlogo|Odkaz na zdrojový kód vytvoreného modelu]] |
Latest revision as of 18:30, 13 June 2020
Táto stránka slúži ako výskumná správa simulácie s názvom „Simulácia zberu jahôd“ k semestrálnemu projektu pre predmet 4IT495 Simulace systémů (LS 2019/2020) na VŠE v Prahe.
Contents
Zadanie
Názov simulácie: Zber jahôd
Autor: Juraj Bačovčin
Typ modelu: Multiagentový
Modelovací nástroj: NetLogo
Popis modelu: Do prostredia tvoreného prechodnou zeleňou, ľubovoľným počtom náhodne rozmiestnených prekážok v podobe stromov a rovnako tak ľubovoľným počtom náhodne rozmiestnených jahôd sú poslaní piati vzájomne súperiaci zberači. Ako to už vyplýva z ich pomenovania, hlavným cieľom týchto zberačov je samozrejme pozbierať čo najvyšší počet jahôd skôr než sa ich zmocnia ostatní, pričom každý jeden z nich má odlišnú stratégiu. Prvý zberač menom Adam sa riadi čisto len svojimi inštinktmi a ďalšie miesto, na ktoré sa vydá, si vyberá výhradne náhodne. Bohumil k tomu pristupuje už o čosi chytrejšie a vydáva sa vždy práve za tou jahodou, ktorá sa k nemu aktuálne nachádza najbližšie. Cyril je zasa raz o niečo pripravenejší a informovanejší, vďaka čomu sa môže najskôr vybrať na miesto, kde by mal byť zhluk jahôd najväčší, všetky ich pozbierať a až tak ďalej pokračovať v zbieraní ostatných jahôd, ktoré sú pri ňom najbližšie. Denis je v porovnaní s ostatnými zákernejší a vyberá si za svoj cieľ vždy práve tú jahodu, po ktorej ide zberač nachádzajúci sa k nemu najbližšie. Na rozdiel od neho posledný zberač menom Erik postráda kompetitívneho ducha a vyberá si vždy jahodu, ktorá je k nemu najbližšie a zároveň po nej nikto iný práve nejde.
Parametre modelu:
- Hustota / počet jahôd
- Hustota / počet stromov
- Veľkosť stromov (prekážok)
- Rýchlosť pohybu zberačov
Cieľ simulácie: Hlavným cieľom tejto simulácie je porovnať rozdielne prístupy k zdanlivo všednej úlohe za účelom nájdenia optimálnej stratégie zberu jahôd (alebo prakticky akýchkoľvek iných surovín) v kompetitívnom prostredí. Okrem toho je však i možné sledovať, ktorá z menovaných stratégií sa teší najväčšiemu úspechu pri iných nastaveniach parametrov, prípadne aké nastavenie parametrov vykazuje najlepšie výsledky pre každého z definovaných zberačov.
Možnosti rozšírení: Do modelu je možné pridať i ďalšie typy objektov (napríklad prekážky s odlišnými tvarmi), parametrov (ako napríklad miera únavnosti, na základe ktorej sa všetci zberači postupne budú spomaľovať až pokiaľ nezastanú úplne za účelom krátkeho oddychu) a v neposlednom rade i zberačov (s ďalšími stratégiami).
Definícia problému
Zbieranie surovín je už od nepamäti súčasťou mnohých ľudských životov. Či už sa jedná o taktický lov a zber rôznych materiálov alebo jedlých plodov z dávnych čias, ktoré údajne tvoria minimálne až 90 percent ľudskej histórie, [1] prípadne moderné problémy spojené s algoritmami pre získavanie surovín v takzvaných strategických hrách v reálnom čase (RTS - real-time strategy), [2] rozhodne ide o tému, ktorej prieskum so sebou môže priniesť mnoho rozdielnych potenciálnych využití. Niet preto divu, že sa jej v kontexte spolupráce na dosiahnutí čo najlepších výsledkov venuje veľa odborníkov z rôznych odvetví, no podstatne menej odborných dokumentov pojednáva o rozličných stratégiách zberu surovín v kompetitívnom prostredí. Táto práca by preto mala poslúžiť ako základ pre porovnanie vybraných dominantných prístupov k zberu materiálov, nájdenie optimálnej stratégie v zjednodušenej abstrakcii danej úlohy a zistenie, ktoré základné parametre môžu mať najväčší vplyv na ich celkovú úspešnosť.
Ako to už vyplýva i z názvu tejto práce, skúmaná úloha bude mať podobu prostého zberu jahôd v neobývanom lese. Ten bude zložený z prechodnej zelene a ľubovoľného počtu náhodne rozmiestnených prekážok stvárnených stromami, ktorý bude možné aj s ich veľkosťou rôzne meniť podľa potreby. Rovnako tak bude možné nastavovať i počet samotných jahôd a rýchlosť pohybu piatich zberačov s rozdielnymi stratégiami zberu, ktorými sú:
- Adam - jahodu, za ktorou sa vydá, si vyberá čisto len náhodne a bez rozmyslu
- Bohumil - bez ohľadu na postup ostatných zberačov si vyberá vždy tú jahodu, ktorá sa pri ňom aktuálne vyskytuje najbližšie
- Cyril - na začiatku v rýchlosti vyhodnotí, v ktorom z kvadrantov mapy sa nachádza najväčší počet jahôd, následne sa za predpokladu, že ho nikto iný nepredbehne, vyberá na víťazné miesto, a potom už len taktiež postupne zbiera jahody, ktoré sa pri ňom nachádzajú najbližšie
- Denis - neriadi sa vlastnými inštinktmi ako ostatní, no namiesto toho si vyberie zberača, ktorý sa pri ňom nachádza najbližšie, a vydáva sa za rovnakou jahodou ako on v snahe predbehnúť ho (v prípade, že si daný konkurent nestihne vybrať svoj cieľ, tak medzitým ide tiež po jahodách, ktoré sú pri ňom najbližšie)
- Erik - namiesto toho, aby priamo súperil s ostatnými konkurentmi, tak si vždy vyberie jahodu, ktorá sa pri ňom vyskytuje najbližšie, a zároveň si ju v danom čase zatiaľ nevybral žiadny iný zberač
Metóda riešenia
Existuje mnoho spôsobov, akými je možné overiť, ktorá z vyššie zmieňovaných stratégií je za rôznych okolností najúčinnejšia. Tým zdanlivo najočividnejším je prevedenie rady skutočných experimentov v reálnom svete s reálnymi ľuďmi, no jednalo by sa o pomerne časovo náročnú a finančne nákladnú metódu. Pre potreby tejto práce teda dáva o dosť väčší zmysel vytvoriť jednoduchý model, s ktorého využitím budú požadované situácie a priebehy zberov jahôd niekoľkokrát odsimulované, pričom získané výsledky môžu byť za predpokladu správnosti implementovaného modelu využité na vyvodenie cieľových záverov.
Z definície problému plynie, že model musí obsahovať niekoľko odlišných entít reprezentujúcich zberačov, ktoré sa neustále na základe ich stratégií rozhodujú, čo za jahodu si vyberú najbližšie, akú cestu k nej zvolia a jak sa vyhnú prítomným prekážkam. Zároveň musia byť schopné reagovať i na situáciu, kedy im konkurenti ich cieľovú jahodu ukradnú skôr, než sa k nej dostanú (nemalo by vonkoncom cenu, aby po nej šli i naďalej). Keď sa k tomu navyše pridá i skutočnosť, že významnú rolu v jednotlivých simuláciách budú zohrávať práve priestorové faktory prostredia (ako napríklad umiestnenie a veľkosť prekážok, pozícia jahôd alebo súradnice zberačov), je podľa názoru autora nepochybne najrozumnejšie zvoliť multiagentový systém. Najideálnejším nástrojom na vytvorenie takého modelu je s ohľadom na možnosti predstavené v rámci predmetu 4IT495 práve NetLogo.
Detailný popis modelu
Ako je možné vidieť i na obrázku vedľa, prostredie modelu je zložené z nasledujúcich hlavných prvkov:
- Mapa, ktorá má veľkosť 33x33 zelených dlaždíc (patches), neprechodné okraje (ak sa ktorýkoľvek zberač vydá dole, nemôže sa objaviť hore), päť osôb s rôznymi farbami reprezentujúcimi jednotlivých zberačov, a užívateľom zadaný počet červených kruhov znázorňujúcich jahody a stromov zohrávajúcich rolu prekážok s danou veľkosťou
- Tlačidlá s názvami Setup a Run, prostredníctvom ktorých je možné pripraviť prostredie mapy na simuláciu a spustiť ju (prípadne ju i pozastaviť)
- Posuvníky, ktorých nastavením je možné meniť jednotlivé parametre modelu (počet jahôd, počet stromov, veľkosť stromov, rýchlosť pohybu zberačov)
- Monitory zobrazujúce aktuálny počet jahôd, ktoré jednotliví zberači odlíšení farbami doposiaľ získali
Agenty modelu
Pre pochopenie funkcionality vytvoreného modelu sa stačí zamerať na takzvané korytnačky (turtles). Hoci by sa na prvý pohľad mohlo zdať, že nimi sú iba jednotliví zberači, pravdou je, že sa ich v modeli vyskytuje viac. Sú to konkrétne:
- trees: Ako to už vyplýva i z názvu, sú to práve prekážky pomenované ako stromy, ktorých jedinými kľúčovými vlastnosťami okrem ich vzhľadu sú súradnice, na ktorých sa nachádzajú, a ich veľkosť. Pri príprave prostredia mapy sú náhodne rozmiestnené tak, aby sa vzájomne neprekrývali, pričom v prípade, že s nimi počas simulácie prídu zberači do kontaktu, tak nemôžu ísť ďalej bez toho, aby ich oblúkom obišli.
- strawberries: Tieto korytnačky reprezentujú jahody, ktorých získanie je hlavným cieľom všetkých zberačov. Okrem vizuálnych vlastností majú iba súradnice, ktoré udávajú, kde sa vyskytujú, a informáciu o tom, či po nich aktuálne ide nejaký zo zberačov. Pri príprave prostredia mapy sú takisto náhodne rozmiestnené, a to tak, aby sa neprekrývali navzájom, no zároveň aby neboli na nejakom mieste, kde by sa k ním nedalo dostať (napríklad v korunách stromov). V prípade, že prídu do kontaktu so zberačmi, zomrú (zmiznú z mapy) a pripočítajú sa k ich aktuálnemu zisku.
- people: Takzvaní ľudia reprezentujú jednotlivých spomínaných zberačov. Okrem vizuálnych vlastností obsahujú opäť súradnice, no zároveň aj informáciu o tom, po akej jahode aktuálne idú, do akej strany sa vyhnú v prípade kolízie s prekážkou a koľko už nazbierali jahôd. Ich identita (a tým pádom do istej miery i chovanie) je daná farbou, pričom na začiatku sú tiež náhodne rozmiestnení tak, aby sa neprekrývali navzájom a aby sa nedotýkali žiadnej jahody či stromu. Od samého počiatku simulácie si postupne vždy na základe ich stratégie vyberajú nejakú jahodu, za ktorou sa vydajú až do doby, než ju získajú alebo im ju niekto ukradne. Musia sa však i vyhýbať stromom, čo všetci dosahujú tým, že ako náhle s nejakým prídu do kontaktu, tak sa oblúkom vyberú buď doprava alebo doľava, kým nemajú zasa voľnú cestu (keby sa náhodou niekde zasekli, tak jednoducho zmenia smer).
Parametre a obory hodnôt modelu
V aktuálnej verzii modelu je možné bez zasahovania do zdrojového kódu nastavovať nasledujúce parametre, ktoré sú definované i v zadaní:
- number-of-trees: Tento celočíselný parameter udáva počet stromov. Minimálna hodnota, ktorú môže naberať, je 1, pričom maximálna hodnota je 60, keďže pri najväčšej možnej veľkosti prekážok by nebolo možné pripraviť prechodnú mapu s vyšším počtom.
- number-of-strawberries Tento celočíselný parameter udáva počet jahôd. Minimálna hodnota, ktorú môže naberať, je takisto 1, pričom maximálna hodnota je tentokrát až 500, čo je vzhľadom na veľkosť mapy podľa názoru autora práce viac než dosť.
- scale-of-trees: Na rozdiel od ostatných parametrov má tento, ktorý udáva veľkosť stromov, povolené iba hodnoty 1.0, 1.5, 2.0, 2.5 a 3.0. Dôvod je skrátka ten, že pri menšej veľkosti by prekážky nepredstavovali žiadny problém pre zberačov, pričom pri väčšej by naopak obzvlášť u maximálneho možného počtu pokrývali väčšinu mapy, čo by ju činilo neprechodnou.
- movement-speed: Tento celočíselný parameter rozhoduje o rýchlosti pohybu zberačov. Minimálna hodnota, ktorú môže naberať, je 1, pričom maximálna hodnota je 100, keďže pri väčšej rýchlosti by už ich prakticky ani nebolo možné efektívne sledovať.
Metódy modelu
Zdrojový kód modelu pozostáva z niekoľkých metód, pričom každá jedna z nich plní nejakú zásadnú funkciu. Jedná sa konkrétne o:
- setup: V tejto metóde sa pripravuje všetko v rámci prostredia mapy a lokálnych i globálnych premenných, čo je potrebné na realizáciu simulácie (viď metódy nižšie).
- set-globals: Táto metóda definuje identity zberačov prostredníctvom čísla vyjadrujúceho nejakú farbu a počiatočné nulové hodnoty jahôd nachádzajúcich sa v jednotlivých kvadrantoch mapy.
- setup-grass: V tejto metóde sa akurát nastaví farba dostupných dlaždíc na zelenú.
- setup-trees: Táto metóda je využívaná na vytvorenie náhodne rozmiestnených korytnačiek reprezentujúcich stromy (viď trees vyššie pre viac informácií).
- setup-strawberries: V tejto metóde sú vytvorené náhodne rozmiestnené korytnačky reprezentujúce jahody (viď strawberries vyššie pre viac informácií).
- setup-people: Táto metóda vytvorí náhodne rozmiestné korytnačky reprezentujúce zberačov (viď people vyššie pre viac informácií).
- get-random-coordinates: Táto metóda je využívaná v rámci viacerých vyššie zmieňovaných metód na nastavenie náhodných súradníc.
- count-strawberries: Táto metóda slúži na úvodné popočítanie jahôd vyskytujúcich sa v jednotlivých kvadrantoch mapy.
- get-identity: Táto metóda akurát priradí vytvoreným zberačom jednotlivé vopred definované identity prostredníctvom farieb.
- go: Táto metoda zabezpečuje priebeh simulácie po príprave prostredia až do doby, než sú pozbierané úplne všetky jahody.
- choose-target: V tejto metóde je definovaný spôsob výberu nadchádzajúcej jahody jednotlivými zberačmi na základe ich identity (podrobnejší popis ich stratégií sa nachádza v definícii problému).
- move-to-target: Táto metóda popisuje pohyb jednotlivých zberačov a očakávané chovanie korytnačiek v prípade, že osoby prídu do kontaktu s nejakou prekážkou alebo jahodou.
Obmedzenia modelu
Ako bolo spomenuté už vyššie, jedným z primárnych obmedzení vytvoreného modelu je nastaviteľnosť parametrov. Vzhľadom na veľkosť mapy totiž nie je možné prekročiť určité hodnoty, inak by sa stala neprechodnou a tým pádom by simulácia nemohla byť uskutočnená. V možnostiach rozšírení zadania sa navyše uvádza i možnosť doplnenia ďalších parametrov (ako napríklad miera únavnosti, na základe ktorej sa všetci zberači postupne budú spomaľovať až pokiaľ nezastanú úplne za účelom krátkeho oddychu), ktoré by mohlo byť zaujímavé implementovať, no pre časové nároky a potreby predmetu museli byť vynechané.
Ďalším obmedzením je inteligencia samotných zberačov. Hoci sa totiž dokážu úspešne vyhýbať prekážkam, nie sú v aktuálnej verzii schopní určiť, či sa im je výhodnejšie vyhnúť zľava alebo sprava, alebo či by nebolo lepšie v prípade, že im v ceste stojí veľa stromov za sebou, vydať trochu inou cestou. Podľa názoru autora by však vzhľadom na to, že po tejto stránke sú na tom všetci zberači rovnako, táto skutočnosť nemala mať v konečnom dôsledku zásadný vplyv na získané výsledky simulácií.
Výsledky
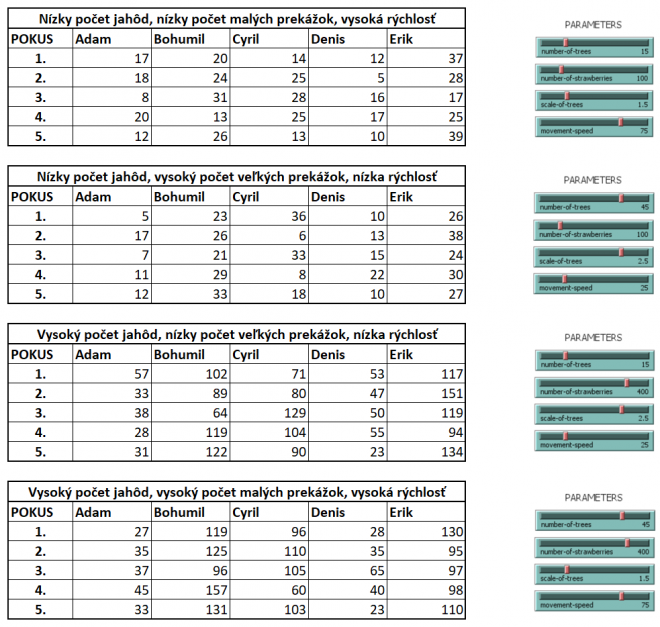
Pred zahájením simulácie bol model v prvom rade riadne otestovaný autorom práce s rôznymi parametrami pri minimálnej rýchlosti zberačov, aby bolo možné jednoznačne overiť, že sa chovajú presne podľa očakávaní. Následne bol už prevedený samotný prieskum, a to vždy s využitím výsledkov piatich simulácií pre štyri najpodstatnejšie kombinácie parametrov (vzhľadom na to, že rýchlosť pohybu má rovnaký vplyv na všetkých zberačov, nastavenie tohto parametru možno podľa názoru autora v rámci dosiahnutia čo najpestrejších výsledkov zanedbať). Výsledky (počet jahôd, ktorý jednotlivé osoby nazbierali) je možné vidieť v nasledujúcich prehľadných tabuľkách:
Adamova stratégia
Niet divu, že zo všetkých zberačov dopadol Adam jednoznačne najhoršie. Stratégia kompletne náhodného výberu jahôd pravidelne obsadzuje posledné a predposledné miesto, pričom iba málokedy sa jej podarí umiestniť vyššie. Nie je zároveň asi ani nijak zvlášť prekvapivé, že najväčšiemu úspechu sa Adam teší pri nižšom počte jahôd, keďže v takom prípade často záleží viac na dobrej štartovnej pozícii ako na inteligencii korytnačky. Na samotných prekážkach naopak nijak zvlášť nezáleží, pričom jednoznačne najlepšie výsledky bude Adam logicky vykazovať s jednou jedinou dostupnou jahodou a najhoršie s maximálnym počtom jahôd. Rozhodne sa teda nejedná o optimálnu stratégiu výberu.
Bohumilova stratégia
Bohumil je v porovnaní s Adamom už na prvý pohľad výrazne šikovnejším zberačom. Hoci je totiž jeho stratégia výberu veľmi jednoduchá, keďže spočíva čisto len v posúdení, ktorá jahoda sa pri ňom aktuálne nachádza najbližšie, teší sa pravidelnému úspechu a takmer garantovanému druhému miestu. Opäť asi nie je veľmi prekvapivé, že pri nižšom počte jahôd má o čosi horšie výsledky, keďže v takom prípade viac záleží na štartovnej pozícii a rozmiestnení prekážok. Čím viac jahôd sa však vyskytuje na mape, tým sú jeho výsledky lepšie. Jednoznačne najlepšie na tom každopádne Bohumil bol pri vysokom počte jahôd a vysokom počte menších prekážok. Jeho stratégia teda patrí medzi tie najoptimálnejšie.
Cyrilova stratégia
Najväčším prekvapením pre autora práce boli Cyrilove výsledky. Hoci má totiž potenciálne najkomplexnejšiu stratégiu, keďže si musí najskôr vybrať, do ktorého kvadrantu sa najviac oplatí ísť, najčastejšie okupoval až tretie miesto a pri nižšom počte jahôd sa pravidelne umiestňoval i nižšie (dvakrát dokonca na poslednom mieste). Pri nižšom počte jahôd a vysokom počte veľkých prekážok mala Cyrilova stratégia najmenej konzistentný úspech, pričom naopak pri vysokom počte jahôd sa bez ohľadu na počet a veľkosť prekážok najviac stabilizovala. Dôvod je s najvyššou pravdepodobnosťou skrátka ten, že je až príliš závislá na hustote jahôd (pokiaľ sú rozmiestnené približne rovnomerne, tak dáva väčší zmysel od samého začiatku ísť po jahodách, ktoré sa pri zberačovi nachádzajú najbližšie) a konaní konkurentov (často sa totiž stávalo, že než sa Cyril dostal na to takzvané najvýhodnejšie miesto, predbehli ho jeho súperi). Táto stratégia teda patrí medzi optimálnejšie skôr v prostredí, ktoré nie je kompetitívne.
Denisova stratégia
Denisova stratégia sa s tou Adamovou najčastejšie delila o posledné a predposledné miesto. Hoci totiž na prvý pohľad dáva zmysel spoliehať sa na rozhodnutia konkurencie a snažiť sa ju predbehnúť, keďže sa Denis stavia do neustáleho súboja o to, či sa k svojmu cieľu dostane skôr ako vybraný konkurent, je logické, že i najviac riskuje. Žiadne z nastaviteľných parametrov nemali nijak zvlášť veľký vplyv na úspech tohto zberača. Najlepšie sa mu bude dariť, keď si zhodou okolností vyberie toho najúspešnejšieho konkurenta, no i tak sa s najvyššou pravdepodobnosťou podľa všetkého ani raz neumiestni na prvom či druhom mieste. Jedná sa teda nepochybne o jednu z najmenej optimálnych stratégií.
Erikova stratégia
Erik bol nepochybne jednoznačným víťazom takmer pri akejkoľvek kombinácii parametrov, ktorý skoro vždy obsadil prvé alebo druhé miesto. Nie nadarmo sa hovorí, že kde sa dvaja bijú, tretí vyhráva. Skutočnosť, že totiž pri výbere vždy uprednostil jahodu, ktorá sa pri ňom nachádzala najbližšie a zároveň po nej nikto iný nešiel, mu zaručila, že sa k väčšine cieľov dostal ako prvý. Prekvapivo ale najlepšie výsledky vykazoval pri nižšom počte jahôd s nízkym počtom malých prekážok a vysokom počte jahôd s nízkym počtom veľkých prekážok, čo by mohlo znamenať, že na Erikovu úspešnosť mal najväčší vplyv práve spomínaný počet stromov. To však nič nemení na tom, že aj v ostatných prípadoch bol aspoň veľmi blízko prvému alebo druhému miestu, takže podľa názoru autora niet najmenších pochýb o tom, že sa vo vytvorenom modeli za akýchkoľvek okolností jedná o najkonzistentnejšiu a najoptimálnejšiu stratégiu.
Záver
Primárnym cieľom tejto práce bolo porovnať päť rôznych prístupov k zberu surovín reprezentovaných jahodami v kompetitívnom prostredí. Zvoleným riešením bolo vytvorenie jednoduchého multiagentového modelu znázorňujúceho zber jahôd piatimi súperiacimi osobami v lese plnom prekážok s využitím nástroja NetLogo. Hoci je výsledný model výrazným zjednodušením reality, ktorý neberie do úvahy mnohé vnútorné či vonkajšie faktory, tento cieľ je podľa názoru autora možné považovať za splnený. S ohľadom na očakávané obmedzenia sa totiž podarilo získať pomerne veľa logických informácií, ako napríklad skutočnosť, že najväčší zmysel dáva vyberať si vždy tie najbližšie umiestnené suroviny, na ktoré sa ostatní nesústredia, pričom naopak najmenší úspech bude takmer určite mať čisto náhodný postup.
Na vytvorený model je možné nadviazať i v budúcnosti jeho rozšírením o ďalšie nastaviteľné parametre, viacero typov máp s rozdielnymi podmienkami, iné prekážky s rôznymi vlastnosťami alebo prípadne i ľubovoľné dodatočné stratégie, ktoré by taktiež mohlo byť zaujímavé porovnať. Zmysel by taktiež podľa názoru autora práce dávalo aj zdokonalenie spomínaného vyhýbania sa prekážkam a celkovej inteligencie agentov, aby mohli včas reagovať i na komplexnejšie situácie (napríklad v prípade, že by Denis zistil, že si vybral nešikovného súpera, tak by mohol sám od seba zmeniť svoj cieľ).
Referencie
- ↑ Hewlett, Barry S. a Lamb, Michael E. Hunter-gatherer Childhoods: Evolutionary, Developmental, and Cultural Perspectives [online]. 2005. Transaction Publishers. [cit. 2020-06-12]. Dostupné z: https://books.google.cz/books/about/Hunter_gatherer_Childhoods.html?id=FLcMONS_7AwC&redir_esc=y
- ↑ Christensen D., Hansen H.O., Hernandez J.P.C., Juul-Jensen L., Kastaniegaard K., Zeng Y. A Data-Driven Approach for Resource Gathering in Real-Time Strategy Games [online]. 2012. Agents and Data Mining Interaction, ADMI 2011, Lecture Notes in Computer Science, vol 7103, str. 304-315. [cit. 2020-06-12]. Dostupné z: https://link.springer.com/chapter/10.1007/978-3-642-27609-5_19