Queueing theory/cs

Teorie hromadné obsluhy (Teorie front)

Jednou z podskupin diskrétních simulací je teorie hromadné obsluhy, v češtině často nazývaná jako "Teorie front".

Úvod

Teorie front zkoumá systémy, na které opakovaně přicházejí sekvence požadavků a jejich výskyt je náhodný. Zjišťujeme tak například potřebnou kapacitu zdrojů, nebo optimální využití výrobních linek. Tato chování se dají nasimulovat do tzv. stochastických modelů. Cílem těchto modelů je analýza stávajících systémů a nalezení nejvhodnějšího způsobu optimalizace. Zároveň se musí optimalizovat množství lidí čekajících ve frontě a vytížení obslužných linek. Pro simulování frontových systémů potřebujeme informace o vstupním toku (např. jak často přijde nový požadavek na server), o frontovém systému, který se vytvoří, pokud požadavek nemůže být ihned vyřízen a organizace obsluhy - počet volných jednotek vykonávající proces obsluhy a jejich popis. Pokud mluvíme o vstupu jako o zákazníkovi, nejedná se o zákazníka v striktním slova smyslu, ale může to být proces, služba, člověk ale i jakýkoliv požadavek čekající na vyřízení.

Příklady SHO

systém	obslužné linky	požadavky
banka	úředníci u přepážky	klienti
výrobní linka	místa na výrobní lince	výrobky
ordinace u lékaře	lékař	pacienti
lyžařské středisko	vleky	lyžaři
benzínová pumpa	čerpací stojany	vozidla
samoobsluha	pokladny, nákupní vozíky	zákazníci

Schéma teorie front

• Objekty vyžadující obsluhu (zákazníci, jednotky, požadavky)
• Množina jednotek přicházející v úvahu pro hromadnou obsluhu
• Časová posloupnost vstupu jednotek
• Množina jednotek čekajících na obsluhu
• Systém realizující obsluhu
• Časová posloupnost výstupu

Základní informace nutné k řešení

Pro analýzu a návrh/optimalizaci systémů hromadné obsluhy je nutné znát základní parametry:

Vstupní tok

Zdroj požadavků, hraje velmi důležitou roli při analýze systémů hromadné obsluhy. I přesto, že v reálném světě jsou všechny vstupy konečné, při analýze systémů hromadné obsluhy se je lze považovat za nekonečné. "Zákazníci" mohou do systému vstupovat jednotlivě nebo hromadně - popis těchto příchodů probíhá pomocí intenzity příchodů (počet požadavků, které do systému přijdou za časovou jednotku), nebo pomocí intervalů mezi příchody. Např. za hodinu přijde průměrně 8 požadavků za hodinu, potom je interval mezi příchody 1/8 hodiny.

• Deterministický příchod požadavků

Intervaly mezi příchody požadavků jsou fixní hodnoty.

• Stochastický

Intervaly příchodů jsou proměnlivé, a proto bývají definovány pomocí pravděpodobnostních rozdělení. Toto rozdělení zjistíme analýzou empirických dat. Pro většinu případů lze využít rozdělení exponenciální [1] a využívá parametr Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda} pro označení intenzity příchodů. Střední hodnota tohoto rozdělení je určena jako:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E(X) = (\frac{1}{\lambda})}
.

Převrácená hodnota Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda} - tedy střední hodnota (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\lambda}} ) vyjadřuje průměrnou dobu mezi příchody požadavků do systému.

Doba trvání obsluhy

Stejně jako při deklaraci intenzity vstupů se využívají popisy deterministické nebo pravděpobobnostní. Nejčastější je opět rozdělení exponenciální, nyní s parametrem Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu} , který označuje intenzitu obsluhy. Střední doba trvání obsluhy dostaneme jako:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle E(X) = (\frac{1}{\mu})}

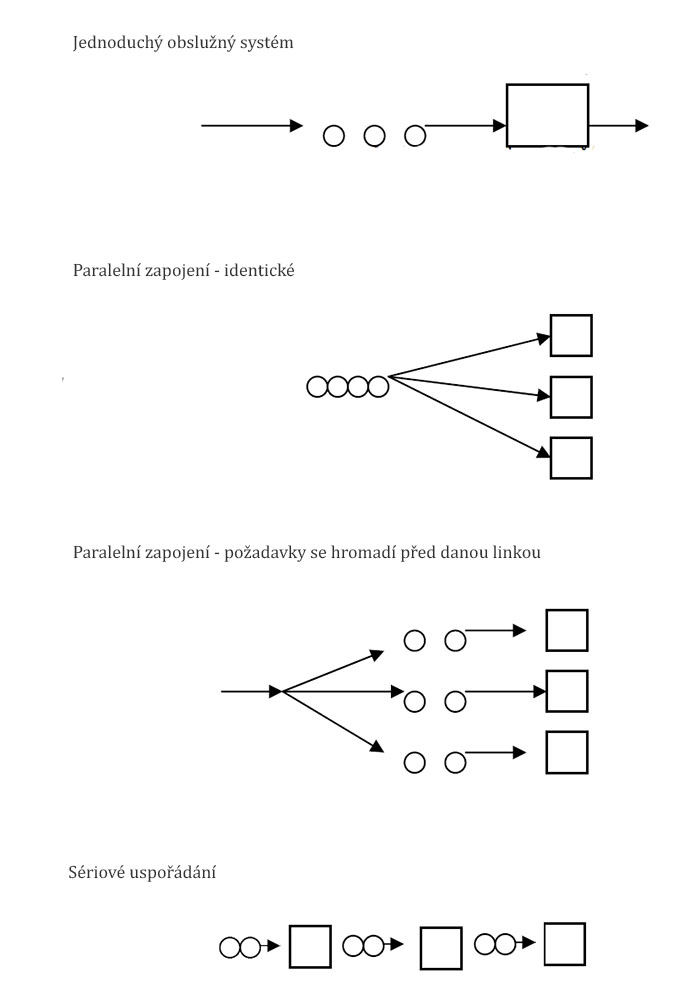
Pokud je v systému zahrnuto více obslužných systémů, mohou se zapojovat sériově nebo paralelně do sítí. Tím se zvýší množství vyřízených požadavků při stejném časovém úseku. U paralelně zapojených systému se klade důraz na jejich zaměření (ne všechny mohou poskytovat stejné služby).

Převrácená hodnota Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu} - tedy střední hodnota Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (\frac{1}{\mu})} označuje průměrnou délku doby trvání obsluhy.

Frontový režim

Ne vždy jsou všechny požadavky hned vyřízeny a z tohoto důvodu se u obslužných linek mohou tvořit fronty "zákazníků" čekajících na vyřízení. Řád fronty určuje, jak probíhá práce s požadavky ve frontě čekajícími. U paralelně zapojených systémů se rozlišují dva typy fronty - jedním typem je fronta, ze které odchází požadavky ke všem obslužným linkám postupně a druhý, kde se před každým obslužným systémem vytváří fronta vlastní.

• FIFO (First-in / First-out)

Požadavky přistupují k obsluze ve stejném pořadí, ve kterém přišly

• LIFO (Last-in / First-out) = LCFS (Last-come / first-served)

Fronta kdy jdou jako první na řadu ty požadavky, které přišly jako poslední

• SIRO (Service in Random Order)

Náhodný způsob výběru

• PRI (Priority queue)

Požadavky přicházejí s předem definovanými prioritami. Pokud se ve frontě sejde víc požadavků se stejnou prioritou, pokračuje podle klasicky definovaného způsobu (např. FIFO, LIFO, SIRO)

Kendallova klasifikace

D.G. Kendall byl anglický statistik a matematik, v 50. letech zavedl notaci pro jednotnou charakteristiku systémů hromadné obsluhy. Jelikož jsou systémy hromadné obsluhy velmi komplexní, je nutné standardizovat jejich značení pro zjednodušení následných výpočtů.

Profesor David George Kendall 15 January 1918 – 23 October 2007 člen the Royal Society (1964)
Anglický statistik a matematik Zasadil se o rozvoj teorie pravděpodobnosti, statistické analýzy tvarů a vzhledu Vyučoval v Oxfordu a Cambridge Ocenění * Royal Statistical Society 1955 the Guy Medal in Silver, 1981 the Guy Medal in Gold * London Mathematical Society 1980 Senior Whitehead Prize, 1989 De Morgan Medal

Jelikož tyto informace nejsou v praxi dostačující, rozšířil se model o další 3 klasifikační třídy.

Na jednotlivé pozice se do modelu dosazují kódy (výsledný model může mít až šestimístný kód - A/B/C/D/E/F)

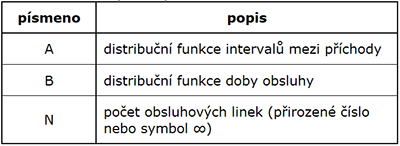
• A

Pravděpodobností rozdělení intervalů mezi příchody požadavků, nejčastěji:

M - exponenciální rozdělení

D - konstantní interval mezi příchody

G - obecné rozdělení se střední hodnotou a směrodatnou odchylkou

• B

Pravděpodobnostní rozdělení doby obsluhy, stejné jako A (M,D,G)

• C

Počet paralelně zapojených obslužných linek

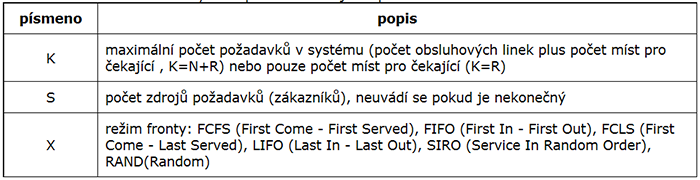
• D

Kapacita obslužného systému (neuvedeno = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \infty} )

• E

Zdroje požadavků (neuvedeno = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \infty} )

• F

Systém fronty (FIFO, LIFO, ...)

Např. zápis systému M/M/1/ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \infty} / Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \infty} /FIFO se zjednodušeně zapíše M/M/1

Analýza systému hromadné obsluhy

Teorie front se v praxi využívá k určení optimální kapacity obslužných systémů. Pokud jdeme například k lékaři na magnetickou rezonanci, musíme se objednávat dlouho dopředu. Rezonance má své časové limity pro obsloužení jednotlivých pacientů (časové náklady aj.), frontu můžeme urychlit, pokud například přidáme další převlékací místnost - jeden pacient je na MRI, druhý pacient se může připravit, po skončení první pacient rovnou odchází do převlékárny, druhý ho střídá. Pomocí teorie front můžeme určit, jak se zrychlí objednávání pacientů, pokud přidáme další přístroj, jaký by měl být minimální časový rozestup v objednávání pacientů aj.

Časové charakteristiky týkající se požadavků

Zjišťujeme především průměrnou dobu požadavků strávenou ve frontě před obsluhou, označujeme symbolem Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T_f} a průměrnou dobu strávenou v systému (celkově) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T} . Průměrnou dobu, kterou střáví požadavek v systému Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (T)} je suma průměrné doby strávené ve frontě Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T_f} a průměrné doby trvání obsluhy Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (\frac{1}{\mu})} , tedy:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T = T_f + (\frac{1}{\mu})}
.

Charakteristiky týkající se počtu požadavků

Zjišťujeme půrměrnou délku fronty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle N_t} nebo průměrný počet požadavků v systému Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle N} . V jednodušších modelech se najde přímý vztah mezi průměrným počtem požadavků v systému (ve frontě) je roven průměrnému času, který požadavek stráví v systému (ve frontě), vynásobenému hodnotou Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda} , tedy:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle N = \lambda T}
,

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle N_t = \lambda T_f}
.

Pravděpodobnostní charakteristiky

Z hlediska optimalizace a matematických analýz jsou velmi důležité matematické charakteristiky. Mezi ty nejdůležitější se řadí pravděpodobnost, že:

• Systém nepracuje (že není využit) nebo naopak, že pracuje
• Nově příchozí požadavek bude muset čekat ve frontě
• V systému je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \eta } požadavků
• Požadavek nebude moci přistoupit k obsluze (systém s omezenou kapacitou míst ve frontě)

Nákladové charakteristiky

Pokud jsme schopni vyjádři náklady na čekání požadavků, prostoje nebo využití obslužných linek, je možné nákladově zefektivnit chod systému

• Minimální náklady na provoz za určitý čas
• Optimální počet obslužných linek v provozu

Analytické vs. simulační řešení

Analytické řešení se zabývá odvozením charakteristik systému a nalezení vzorců, které se pak používají stále dokola. Například počet obslužných linek Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle c} , intenzita příchodů Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda} , nebo intenzita obsluhy Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu} . Analytické řešení bývá velmi uživatelsky příjemné. Výsledky jsou k dispozici velmi rychle, ale dají se použít pouze pro ty jednodužší případy. Tedy není vhodné pro sériově řazené obslužné linky, stejně jako modely s například omezenou trpělivostí požadavků, systém s PRI systémem fronty aj.

Pro případy modelů Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M/M/1} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M/M/c} se využívá systémových simulací. Napodobuje se chování reálného systému - výhoda je v tom, že výsledky, které bychom normálně sledovali i několik měsíců jsou k dispozici během pár minut. Tímto způsobem se testují téměř všechny navrhované systémy hromadné obsluhy.

Exponenciální model Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M/M/1}

Pro optimalizaci a stabilizaci systému je důležité, aby byla splněna základní podmínka, a to, že intenzita příchodů Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda} je nižší než intenzita obsluhy Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu} , tedy intenzita provozu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \rho > 1} .

Předpoklady

Pouze jedna obslužná linka

Intervaly mezi příchody mají exponenciální rozdělení s parametrem Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda}

Doba trvání obsluhy je náhodná veličina s exponenciálním rozdělením s parametrem Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu}

Neomezená kapacita systému

Neomezený zdroj požadavků

Režim fronty FIFO

Systém má dva parametry - intenzitu příchodů Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda} a intenzitu obsluhy Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu} . Pravděpodobnost, že v systému není žádný požadavek (=obslužný systém není v provozu):

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_0 = 1 - \frac{\lambda}{\mu}}
.

Tedy pravděpodobnost, že v systému je alespoň 1 požadavek (=obslužný systém je v provozu):

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \rho = \frac{\lambda}{\mu}}

Prvek Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \rho} označuje intenzitu provozu systému hromadné obsluhy. Tato hodnota udává zároveň pravděpodbobnost, že nově příchozí požadavek do systému bude muset čekat ve frontě.

Pravděpodobnost, že v systému je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n} požadavků a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (n-1)} požadavků čeká ve frontě:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_n = p_0 \rho^n = (1- \rho)\rho^n}

Průměrná doba, kterou požadavek stráví v systému a ve frontě je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle T = \frac{1}{\mu - \lambda}} , tedy

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle  T_f = T - \frac{1}{\mu} = \frac{\lambda}{\mu(\mu - \lambda)}}
.

Průměrný počet požadavků v systému Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (N)} , a ve frontě Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (N_f)} :

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle  N = \lambda T =  \frac{\lambda}{\mu-\lambda}}
, 

odtud

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle  N_f = \lambda T_f = \frac{\lambda^2}{\mu(\mu-\lambda)} }
.

Exponenciální model Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M/M/c}

Podmínkou pro optimalizaci je intenzita celého provozu systému Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \rho = \frac{\lambda}{c \mu} <1}

Předpoklady Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M/M/c}

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle c} identických obslužných jednotek v systému

Intervaly mezi příchody požadavků mají exponenciální rozdělení s parametrem Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda}

Doba obsluhy na každé z linek je náhodná veličina s exponenciálním rozdělením s parametrem Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu}

Neomezená kapacita systému

Neomezený zdroj požadavků

Režim fronty FIFO

Systém má tři parametry - počet obslužných linek Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle c} , intenzitu příchodů Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \lambda} a intenzitu obsluhy Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu} u každé z obslužných linek. Intenzita obsluhy je u každé z linek vlastní, a proto je výsledek celého systému roven součinu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle c} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mu} . Základní proměnné: poměr intenzity příchodů a individuální intenzity obsluhy Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle r = \frac{\lambda}{\mu}} intenzita provozu celého systému Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \rho = \frac{\lambda}{c\mu}} (=průměrné využití všech obslužných linek systému)

Pravděpodobnost, že v systému není žádný požadavek (=obslužný systém není v provozu):

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_0 = [(\sum\limits_{k=0}^{c-1}\frac{r^k}{k!}) + \frac{cr^c}{(c-r)c!}]^{-1}}
.

Tedy pravděpodobnost, že v systému je alespoň n požadavků, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n&\le&c} (=obslužný systém je v provozu):

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_n = \frac{r^n}{n!}p_0, n&\le&c}
.

Pravděpodobnost, že v systému je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n} požadavků (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle n>c} ), všechny systémy jsou tedy v provozu:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p_n = \frac{r^n}{c!c^{n/c}}p_0, n>c}
.

Průměrná doba, kterou požadavek stráví v systému Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (T)} a ve frontě je Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (T_f)} :

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle  T_f = \frac{r^c \mu}{(c-1)!(c\mu-\lambda)^2}p_0, n>c }
,

tedy

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle  T = T_f + \frac{1}{\mu}}
.

Průměrný počet požadavků v systému Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (N)} , a ve frontě Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (N_f)} :

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle  N = \lambda T}
, 

odtud

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle  N_f = \lambda T_f }
.

Pravděpodobnost, že nově příchozí požadavek bude zařazen do fronty,

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P_f = \frac{r^c c}{c!(c-r)}p_0}
.

Optimalizace modelu Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle M/M/c}

Optimalizace probíhá na úrovni nalezení konkrétní hodnoty Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle c} , tak aby byly minimalizovány náklady na provoz celého systému. Proměnné:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k_1} náklady na pobyt jednoho požadavku v systému za jednotku času

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k_2} náklady na provoz jedné obslužné linky v systému za jednotku času

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle N} průměrný počet jednotek v systému

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle c} počet paralelně řazených obslužných linek

Nákladovou funkci definujeme:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle NF(c) = K_1 N + K_2 c}
.

Rovnice se skládá ze dvou částí: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K_1N} a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K_2 c} . První část (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K_1N} ) značí náklady na pobyt požadavku v systému za určitý čas a druhá část (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K_2 c} ) charakterizuje náklady na provoz všech obslužných linek za časovou jednotku. Při navýšení obslužných systémů dojde ke zvýšení nákladů a sníží se průměrný počet požadavků v systému a naopak.