Extensive form/cs

Úvod

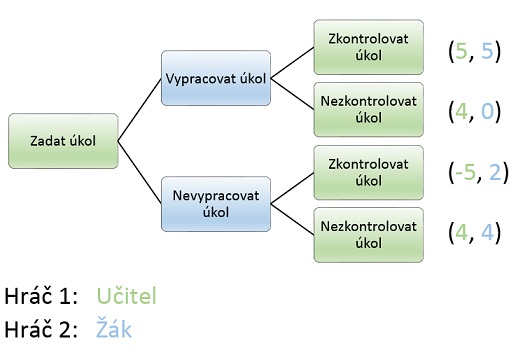
Klasická matice hry v normálním tvaru je vhodná pro grafické znázornění situací, kdy se hráči rozhodují ve stejný okamžik. V případě, kdy se hráči střídají v rozhodování, taková reprezentace již není dostačující, proto se používá tzv. rozšířená forma, která tyto situace zobrazuje pomocí rozhodovacího stromu.

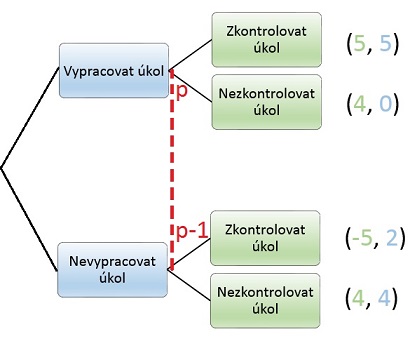
Obrázek výše představuje jednoduchou "hru", kdy se žák rozhoduje, zda vypracovat či nevypracovat domácí úlohu zadanou učitelem. Užitky (vpravo v závorkách) se uvádějí vždy za posledním rozhodovacím krokem. Rozhodovací krok představuje každý uzel v grafu.

Akce vs. strategie

Akcí je právě jedno rozhodnutí. U statických her se rozhoduje zda je výhodnější provést to, či ono, což je samo o sobě výsledkem. Dynamické hry obsahují více uzlů, tedy více akcí ke kterým je nutné učinit rozhodnutí, a to ještě před zahájením samotné hry. Hovoříme tedy o strategii. Strategie je plán akcí pro veškeré situace, které mohou nastat.

Metody řešení

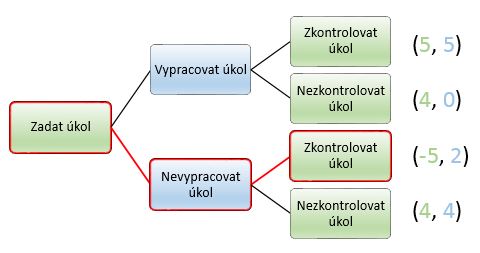
Nejčastěji se používá stejná metoda nejlepších reakcí jako v případě statických her s tím rozdílem, že se neporovnávají akce, nýbž strategie. Strategii lze vyjádřit zvýrazněním cesty od kořene grafu až k jednomu z jeho posledních potomků.

V předešlém případě značíme červeně vyznačenou strategii takto: <Zadat úkol, Zkontrolovat úkol>; <Nevypracovat úkol> nebo zkráceně: <Z, Z>; <N>. Tato strategie však není kompletní, protože v ní nejsou zahrnuty veškeré situace, které mohou nastat, tj. pokud se žák rozhodne vypracovat úkol, učitel nebude mít pro tuto možnost stanovenou strategii. Pojďme si tedy ukázat, jak postupovat správně při hledání optimálního řešení dynamických her.

Zpětná indukce

Předchozí příklad je příkladem hry s nekompletní informací, tj. v situaci, kdy se učitel rozhoduje zda úkol zkontrolovat, či nikoliv, tak nemá informaci o tom, zda žák úkol vypracoval nebo ne. K tomuto typu příkladů se ještě vrátíme, ale pro začátek si vysvětlíme metodu zpětné indukce na příkladu tzv. Escalation game.

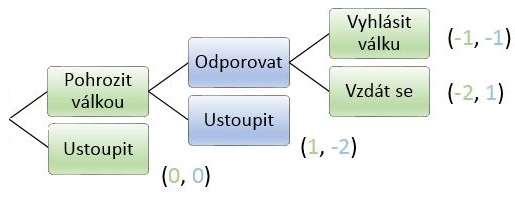
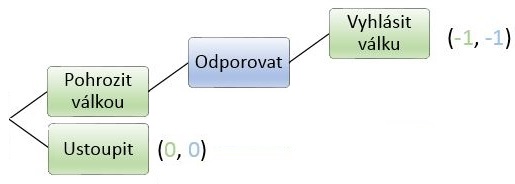
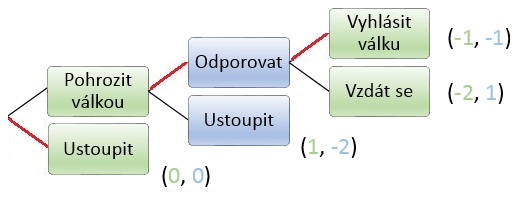
Dva státy se dostanou do sporu o území. Jeden ze států může buď pohrozit válkou nebo přenechat území druhému státu. Druhý stát se může nechat hrozbou zastrašit a území se vzdát nebo odporovat (také pohrozit válkou). První se může vzdát a nebo skutečně vyhlásit válku. Graficky lze hru znázornit takto:

Postupujeme od posledního rozhodovacího uzlu směrem ke kořenu stromu, přičemž můžeme daný rozhodovací uzel považovat za samostatnou "podhru" nezávislou na zbytku stromu a řešit ji stejně jako statickou hru.

Stát 2 se může v posledním kroku rozhodnout pro válku nebo mír, za cenu toho, že bude vypadat jako zbabělec a navíc přijde o území bez snahy ho získat. Užitek -1 je vyšší než -2, proto se stát 2 rozhodne pro válku. Nyní můžeme postoupit v rozhodovacím stromu o úroveň výše a opět řešit "podhru" jako statickou.

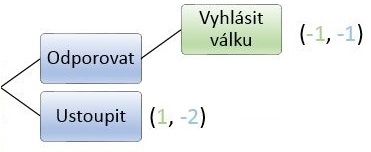
Stát 1 je na řadě a má možnost odporovat nebo ustoupit, když bude odporovat, tak již ví, že stát 2 mu vyhlásí válku a užitek obou států bude -1. Pokud Stát 1 ustoupí, jeho užitek bude -2, protože přijde o území bez snahy ho získat a bude vypadat jako zbabělec. Stát 1 tedy zvolí odpor.

Stejně postupujeme v posledním kroce: 0 je víc než -1, proto Stát 1 raději ustoupí. Sice přijde o území, ale alespoň ušetří životy lidí, kteří by padly v jinak nevyhnutelné válce.

Výsledek značíme jako strategii ve všech možných situacích: <Ustoupit, Vyhlásit válku>; <Odporovat>

  Pomůcka: Strategie musí vždy obsahovat stejný počet akcí jako je počet uzlů v rozhodovacím stromu!

Hry s (ne)kompletními informacemi

Vraťme se k příkladu uvedenému na začátku tohoto textu. Žák má možnost domácí úkol (ne)vypracovat a učitel (ne)zkontrolovat. Po tahu žáka učitel neví v jaké části stromu se nachází, jeho znalost předchozích akcí je nekompletní. Přerušovaná čára značí jeden informační set, tj. jeden rozhodovací uzel. Ať už se hráč nachází v jedné či druhé části, jeho rozhodnutí bude vždy stejné, protože neví v které části se nachází.

Z toho plyne, že hra s nekompletní informací musí splňovat tyto podmínky:

• Alespoň jeden z hráčů nezná celou historii hry
• Alespoň jeden informační set není jedináček (obsahuje alespoň dva uzly grafu)
• Všechny uzly v rámci informačního setu musí vést ke stejným rozhodovacím možnostem (pokud jeden uzel vede k možnostem nahoru, dolů a druhý k nahoru a doprava, pak se jedná o dva různé informační sety)

Postup řešení

Grafické znázornění je téměř stejné jako u hry s kompletní informací. Pouze se navíc přidá přerušovaná čára značící, že se jedná o jeden informační set a pravděpodobnost p a p-1, že se nacházíme v horní/dolní části stromu, tj. žák vypracoval/nevypracoval domácí úkol (viz níže).