Monte Carlo method

Introduction and history

Monte Carlo method is a stochastic method using pseudorandom numbers. We can also say it is a class of algorithms for the simulation of systems. We can use it for solving mathematical problems as calculating integrals, particularly multidimensional where conventional methods are not effective. This method has wide range of application - from simulation experiments through computation of definite integrals up to for example solving differential equations. The basic idea of this method is very simple. We want to determine the mean value of the variable that is the result of random action. Let's imagine creation of a computer model of that action and after a sufficient amount of simulations, data may be processed by conventional statistical methods, for example to determine the average and standard deviation. Monte Carlo method was formulated and also used during World War II by scientists John von Neumann and Stanislav Ulam in the United States in the development of atomic bomb. A research of neutron behavior and its feasibility of penetration various substances raised the problem of how to determine the percentage of neutrons in a spray that penetrates for example the water tank of certain dimensions. It wasn't possible to find a practical method to predict further behavior of individual neutron, to predict the entire further "history of his life." Neumann and Ulam used for modeling the prediction of "history of neutron life " Monte Carlo method inspired in roulette wheel technique (from here was the idea for the name Monte Carlo). Using this method it is possible to predict the trajectory of each neutron of the given bundle. Simulation of neutron motion wandering in water and randomly colliding with atoms of hydrogen and oxygen was done as follows:

"Is known that random event - that neutron is absorbed by hitting the hydrogen atom - will occur in one of hundred possible cases on average. To map the route of neutron is spinned the roulette wheel divided into one hundred parts, and among them only one part is indicating the "neutron absorption by a hydrogen atom." If the roulette wheel stops on that part, it indicates the "end of life" of neutron. In opposite case is possible by the another roulette wheel to determine the direction and speed of the neutron after collision. Then with another roulette wheel is possible to determine the trajectory that neutron will take before the next collision occurs. Simulation of "history of life" of neutron is performed as long until the neutron is absorbed, or until it lose such energy that the final exit of the neutron is no longer interesting for us, or until the neutron manages to escape without damage from the tank. When we will make a large amount of such simulations, we get more or less accurate information about percentage of neutrons that have managed to escape from the tank. The accuracy of this method is determined by mathematical-statistical methods of estimation theory." František Fabian, Zdenek Kluiber, Metoda Monte Carlo a možnosti jejího uplatnění, Praha: Prospektrum, 1998, page.13-14

Despite fact this is a very simplified example the nature of the Monte Carlo method is described close enough. The simulation would be of course very time consuming, in case it is actually necessary always spin the roulette. However, the authors worked at a time when the development of information technology was already in full progress, therefore they could use for these simulations simple computers (compared to current ones) that simulation time significantly shortened. The basic principle of Monte Carlo method has been spoken in 1777. In this year the French natural scientist Georges de Buffon formulated his famous needle problem - known as Buffon's task. It determines the value of the number π by random throwing a needle on paper with painted equidistant parallels. Very simply, it is an experiment, when he throws a needle on sheet of paper. Paper is divided by parallel lines and the needle is the same size as the distance between the lines. The result is that the probability of the needle crosses one of the lines is 2 / π. From this can be deduced π value. In 1901 Lazzerini made 34 080 needle throws and got for number π value 3,1415929 which was really amazingly good result. This method was at first used in solving the physics problems, which were before then practically unsolvable. Gradually, with the development of computer technology and modeling theory, it began to be used in solving complex problems from such areas like technology, economy, activity of call centers, traffic management and in solving problems in mathematics itself. Monte Carlo method is useful especially wherever there is the solution of the problem in some way dependent on the probabilities.

Monte Carlo Method

With Monte Carlo method we solve probabilistic and deterministic tasks using many times repeated random iterations. The solution is based on the fact that we construct probabilistic task, which has identical solution with the original task. The obtained solution has a probabilistic nature. Monte Carlo method can be divided into two groups according to the procedure of the solution or let say there are two possible approaches to solving problems by Monte Carlo method - the "geometric method" and the "calculation based on the estimation of certain characteristics of the random variable".

Geometric method

The geometric approach we have already met in the Buffon's task. Now, on a simple example let me show what other way can experimentally determine the value of π. To solve we use random number generator software Microsoft Excel (RAND function).

Calculation of π value

Is given unit square, which is inscribed with circular sector (see picture n.1). Using geometric approach we experimentally determine the value of π. 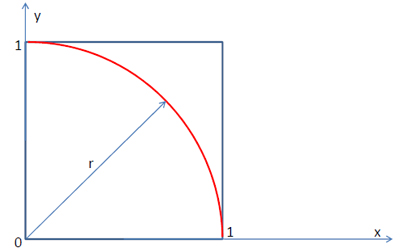Picture n.1

Define event A - randomly selected point of the unit square is located in a circular sector. Based on the geometric probability, we can write the probability of the event A:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle P(A)=\frac{\pi}{4}} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \dfrac{2}{ c + \dfrac{2}{ d + \dfrac{1}{2} } }}