Difference between revisions of "Robotic Vacuum Algorithms Simulation (kulv05)"
| Line 113: | Line 113: | ||
[[File:Kulv05_standartspiral_algorithm.nlogo]] | [[File:Kulv05_standartspiral_algorithm.nlogo]] | ||
| + | |||
| + | |||
| + | ---- | ||
| + | ==Spiral + Horizontal Zigzag== | ||
| + | |||
| + | A robot vacuum cleaner utilizing the spiral and horizontal zigzag algorithm demonstrates high patch coverage for indoor cleaning. The algorithm is an improvement on the previous spiral approach by adding a horizontal zigzag traversal. This algorithm combines two key approaches: spiral trajectory and horizontal zigzag trajectory. Spiral traversal allows the robot to start at the random start pount of the room and gradually expand the cleaning zone to cover the entire area. | ||
| + | |||
| + | The spiral algorithm is the same as in the stantard one. The horizontal zigzag adds extra coverage as the robot moves from left to right and from right to left, allowing it to “fill in” possible gaps that might have been left by a simple spiral traversal. For example, while in a classic spiral the robot misses some cells due to the abrupt transition between layers, the zigzag motion compensates for this by providing a more thorough cleaning. | ||
| + | |||
| + | [[File:Kulv05_spiralhorizzigzag.gif]] | ||
| + | |||
| + | [[File:Kulv05_spiral_horiz_zigzag_algorithm.nlogo]] | ||
---- | ---- | ||
==Zigzag== | ==Zigzag== | ||
| Line 274: | Line 286: | ||
The Spiral algorithm is a reliable choice for tasks that prioritize systematic coverage, but is not competitive compared to more modern and efficient cleaning strategies. Its excessive time requirements and high energy consumption make it not the greatest choice for most scenarios. While it achieves moderate trash collection, this is not enough to justify its inefficiencies. | The Spiral algorithm is a reliable choice for tasks that prioritize systematic coverage, but is not competitive compared to more modern and efficient cleaning strategies. Its excessive time requirements and high energy consumption make it not the greatest choice for most scenarios. While it achieves moderate trash collection, this is not enough to justify its inefficiencies. | ||
| + | |||
| + | ---- | ||
| + | ====Spiral + Horizontal Spiral Results==== | ||
| + | |||
| + | [[File:Kulv05_spiral_horiz_zigzag_stats.png]] | ||
---- | ---- | ||
| Line 369: | Line 386: | ||
[[File:Kulv05_standartspiral_algorithm.nlogo]] | [[File:Kulv05_standartspiral_algorithm.nlogo]] | ||
| + | |||
| + | [[File:Kulv05_spiral_horiz_zigzag_algorithm.nlogo]] | ||
[[File:Kulv05_standart_zigzag_algorithm.nlogo]] | [[File:Kulv05_standart_zigzag_algorithm.nlogo]] | ||
[[File:Kulv05_astar_algorithm.nlogo]] | [[File:Kulv05_astar_algorithm.nlogo]] | ||
Revision as of 18:19, 26 January 2025
Problem definition
The primary objective of this simulation is to thoroughly analyze and compare different movement algorithms designed for a robotic vacuum cleaner.
The focus is to evaluate their effectiveness by focusing on key performance metrics, including cleaning speed, power consumption, and overall performance.
Method
The simulation will be developed using NetLogo, an agent-based modeling platform. NetLogo is ideal for simulating complex systems with numerous interacting agents (in case of this simulation - a robot vacuum and pieces of trash).
Efficiency Metrics for Trash Collection
To evaluate the performance of trash collection systems, we use the following metrics: Time Efficiency in Time, Power Efficiency, and Overall Efficiency. Each metric is designed so that lower values indicate better performance.
1. Time Efficiency This metric measures how many ticks are required to collect a unit of trash. A lower value indicates faster trash collection.
Time Efficiency = Ticks needed to finish cleaning/Collected Trash
2. Power Efficiency This metric measures how much energy is consumed to collect a unit of trash. A lower value indicates better energy efficiency.
Power Efficiency = Energy / Collected Trash
3. This metric combines both time and energy efficiency into a single value. A higher value indicates better overall performance.
Overall Efficiency = CollectedTrash /(Ticks needed to finish cleaning × Energy)
Metrics such as ticks needed to finish cleaning and energy are also used for the comparison, the lower - the better.
Room setup
The room and furniture was created using patches.
I originally wanted to make the furniture using agents as you can see in the assigment, however after using this method I realized that than making each furniture using agents is not an ideal solution. First of all, furniture is static and does not have to move around. Also, patches are easier to visualize using their color or shape because agents have a limited shape options.So this is why it was easier to arrange furniture as a set of patches.
The room itself was imagined as a living room with a coffee table in the middle and two sofas around it.
Trash placement
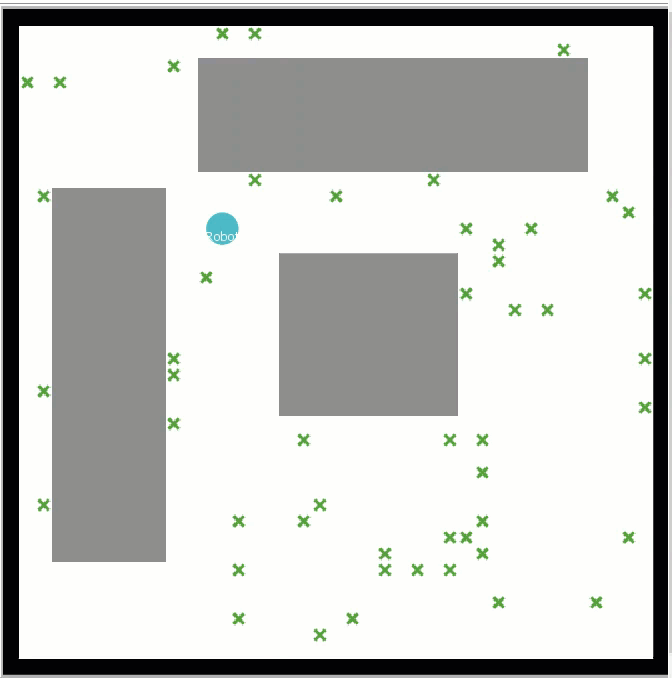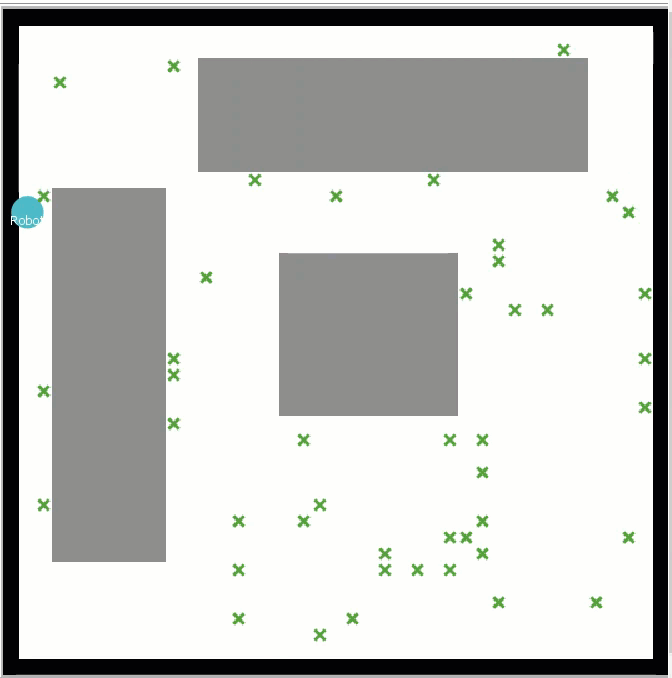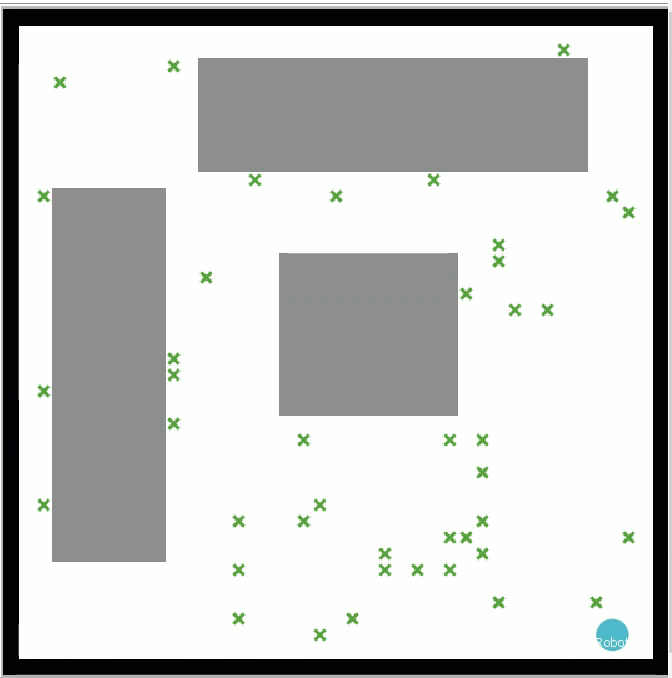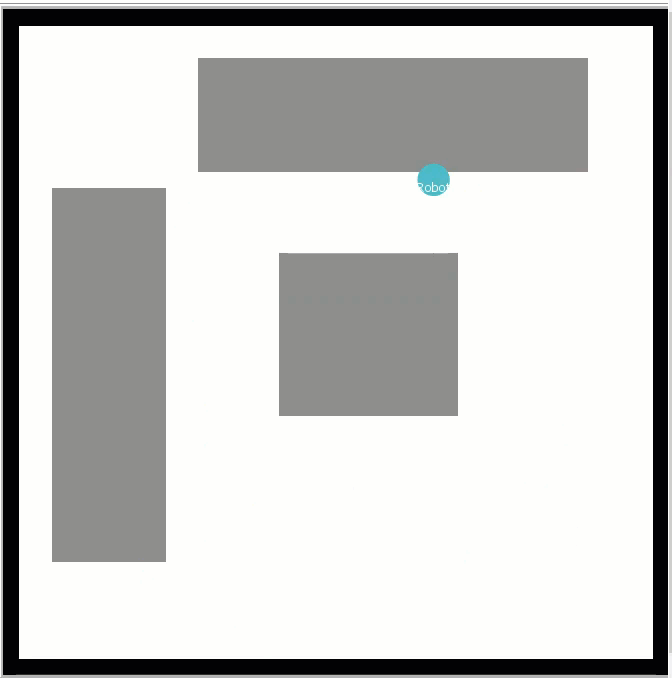
A procedure named setup-trash is designed to simulate the placement of trash in the environment. It creates 50 trash agents, represented by green "x" shapes, and attempts to place them on random white patches of the room that also do not already contain trash. If a suitable patch is found, the trash agent is positioned there, and the patch is marked as occupied; otherwise, the trash agent is removed. Then, the total number of successfully placed trash agents is counted and stored in the variable total-trash.
Vacuum setup
Setup-robot function creates a single robot agent. The robot is represented as a cyan-colored circle with a size of 2. It is initialized with an energy level of 0. The robot is placed on a randomly selected white patch that does not contain trash. The robot is also labeled with the text "Robot".
Energy
Energy is a parameter of a robot that starts with a 0 and acumulates a specific value over the course of the simulation. Different actions recuire different energy usage. For example, every step forward is considered to have a value of 1, every turn, because the brushes are used differently when turning, has a value of 0.5 and finally, the hardest action of all, trash collection, has a value of 2.
Model
Random Walk
The movement algorithm characterized as "random walk" implies that an object moves through space without a predetermined trajectory and/or target. In this case, the object moves in an arbitrary direction until it encounters an obstacle, such as a wall or a piece of furniture. Upon detecting an obstacle, the object selects a new random direction to continue its movement. And the cycle continues until all the trash is collected.
This approach does not involve any strategy or route optimization, which means the object may spend a significant amount of time moving within a limited space, constantly changing direction after each collision. This results in a "wandering" effect, where the object chaotically rebounds off walls without reaching a specific goal or destination.
The random walk algorithm, despite its' negative sides, is still widely used because it is one of the simplest algorithms that can be used in robot vacuum cleaners. Its main advantage is the simplicity of implementation. This approach does not require complex calculations, room mapping or expensive sensors, making it ideal for budget models.
The random walk algorithm has significant disadvantages that limit its effectiveness. Firstly, the robot can repeatedly clean the same areas while other areas remain untidy. This results in longer cleaning time and wasted energy. Secondly, in large rooms, the robot can wander around for hours without completing the task. Lastly, the algorithm does not take into account the structure of the room (e.g., walls or furniture) and does not optimize the route, making it less efficient than more advanced methods.
File:Kulv05 randomwalk algorithm.nlogo
Wall-to-wall
The "Wall-to-Wall" is an algorithm that involves the robot vacuum first finding a wall and then moving along it, cleaning the perimeter of the room. This approach is effective for removing debris in corners and along walls, where dirt often accumulates. However, if this algorithm is used in its original form or on its own, it is not optimal for a complete room cleaning. The main issue is that the robot ignores the central part of the room, where debris may also be present. As a result, even if the perimeter is perfectly clean, the center of the room remains uncleaned, significantly reducing the overall efficiency of the cleaning process. Thus, as you can see in a showcase of the simulation below, in its pure form, the "Wall-to-Wall" algorithm cannot be considered an optimal solution for thorough room cleaning. The trajectory was inspired by the "Improving robotic vacuum cleaners" article. [1]
The algorithm, due to its nature, constanly loops near the walls, so to analyze the effitiency I decided to stop after 1000 ticks and apply all the formulas to see the results. It does not finish after all the trash was collected, but after 1000 ticks have passed.
File:Kulv05 standart walltowall algorithm.nlogo
Wall-to-wall + Horizontal Zigzag
The "Wall-to-wall" algorithm enhanced by the Horizontal Zigzag algorithm is a combination of algorithms that help us reach the goal - collect all the trash in the room. The "Horizontal Zigzag" logic was specifically made as a support function for this project's not ideal trajectories that do not cover the whole room itself.
The robot starts moving forward the already discussed "Wall-to-wall" algorithm. The robot keeps track of how many room corners it has passed. After completing two full loops (8 corners) and then it switches to the next stage — Horizontal Zigzag.
At this stage, the robot moves in a zigzag pattern across the room. It starts moving either right or left until it reaches a wall or obstacle. When the robot reaches a wall, it moves up (or down) one row and changes direction. If the robot reaches the top boundary of the room, it switches to moving downward. If it reaches the bottom boundary, it switches to moving upward. It covers the patches that were not visited before, ensuring that the trash can be collected.
The algorithm ensures that the robot covers the entire room, including hard-to-reach areas like corners and the center. This is crucial for tasks like cleaning, where missing even a small area can be problematic. By combining wall-following and horizontal zigzag movements, the robot systematically explores the space, minimizing the chances of leaving any trash behind.
File:Kulv05 walltowall horiz zigzag algorithm.nlogo
Spiral
A spiral trajectory in the context of robotic vacuum cleaner algorithms is a strategy in which the robot moves along an expanding spiral, starting from a point and gradually increasing the radius of movement until it reaches the boundaries of the room or encounters an obstacle. This approach is based on the idea of systematically covering the area to minimize missed spots and ensure efficient cleaning.
The inspiration for this trajectory was drawn from the article "Improving Robotic Vacuum Cleaners" [1]. Additionally, the article "A Performance Comparison of Coverage Algorithms for Simple Robotic Vacuum Cleaners" highlights that the spiral algorithm, while initially effective, tends to degrade into a "wall-to-wall" algorithm in constrained environments.
The spiral trajectory is highly effective in open, unobstructed spaces when it starts in a central point. However, in rooms cluttered with furniture and starting in a random place, it is not the optimal choice.
This degradation results in the algorithm inheriting the limitations associated with such approaches. The article recommends combining the spiral algorithm with another algorithm to mitigate these drawbacks, a strategy that will be demonstrated in the next algorithmic showcase [4].
Here you can see an algorithm where the robotic vacuum follows the spiral trajectory until it reaches the walls and the ticks are less then 2500. This can show the standart speral trajectory best and that is why i decided to make this choice. Although, I did a few experimentations that i did not include.
If we imagine the spiral algorithm, when it moves in this specific way foe too long, it becomes the wall-to-wall algorithm and inherites its issues. This is why I decided to experiment with an alternative approach to the spiral algorithm by implementing a reverse spiral after the initial algorithm is not effective anymore. While the reverse spiral appears logically consistent, in practice, it often proves less effective. This is particularly evident in scenarios where the robot begins to re-cover areas that have already been cleaned. Although this algorithm may have utility under specific conditions, in my practical implementation, it demonstrated inferior performance compared to the random-walk algorithm. This suggests that in real-world applications, the reverse spiral may be outperformed by other cleaning strategies. What came to the metrics, they were worse than the values of the random walk algorithm and this is why I chose to mention it, but not include it into the report.
File:Kulv05 standartspiral algorithm.nlogo
Spiral + Horizontal Zigzag
A robot vacuum cleaner utilizing the spiral and horizontal zigzag algorithm demonstrates high patch coverage for indoor cleaning. The algorithm is an improvement on the previous spiral approach by adding a horizontal zigzag traversal. This algorithm combines two key approaches: spiral trajectory and horizontal zigzag trajectory. Spiral traversal allows the robot to start at the random start pount of the room and gradually expand the cleaning zone to cover the entire area.
The spiral algorithm is the same as in the stantard one. The horizontal zigzag adds extra coverage as the robot moves from left to right and from right to left, allowing it to “fill in” possible gaps that might have been left by a simple spiral traversal. For example, while in a classic spiral the robot misses some cells due to the abrupt transition between layers, the zigzag motion compensates for this by providing a more thorough cleaning.
File:Kulv05 spiral horiz zigzag algorithm.nlogo
Zigzag
The algorithm, using the trajectory inspired by the "Improving robotic vacuum cleaners" article [1], due to its nature, constanly loops near the left, so to analyze the effitiency I decided to stop after 1000 ticks and apply all the formulas to see the results. It does not finish after all the trash was collected, but after 1000 ticks have passed.
A zigzag algorithm uses the trajectory in which the robot moves around a room by alternating its direction of travel at an angle, typically 90 degrees, thereby creating a zigzag pattern. This approach allows the robot to cover the room area more evenly, especially in environments where there are obstacles or furniture.
One of the advantages of the zigzag trajectory includes uniform area coverage, adaptability to obstacles, and ease of implementation. However, in some cases, the robot may pass through areas that have already been cleaned, reducing overall efficiency.
However, because we start at a random point rather than a corner, this algorithm will not always collect all the garbage or have the best path.
File:Kulv05 standart zigzag algorithm.nlogo
Combined Zigzags
SLAM (simultaneous localization and mapping)
[2]
A*
A robot vacuum cleaner using the A* algorithm, unlike the other examplex, does not follow a predetermined trajectory. Instead, it employs an intelligent A*-based planner that helps calculate the shortest path from the robot's current position to the nearest trash agent, while taking into account obstacles such as walls or furniture. [3] The planner analyzes possible paths from the robot's current location to the target, compares them, and selects the fastest and most efficient route. The robot is then provided with a list of cells to follow to reach the goal. The robot moves along the proposed route, collects the debris, and then repeats the process to search for the next target. This approach makes cleaning more systematic and efficient.
The algorithm works by combining two main elements: the actual cost of the path the robot has already traveled and the estimated (heuristic) cost of the remaining distance to the target. This helps the robot make smart decisions about which direction to move in. I used a heuristic function, such as the Manhattan distance, to estimate how far the robot is from the goal. The Manhattan distance is simple yet effective — it adds up the horizontal and vertical distances between the robot and the target. Based on that, the algorithm always chooses the path with the lowest total cost, which means the robot avoids unnecessary movements and saves time. It is important to mention that the A* algorithm considers obstacles like walls or furniture and excludes them from possible routes. This allows the robot to find the best way around obstacles and clean efficiently, even in complex rooms.
I want to mention that it took a lot of time and countless tries to create a algorithm as complex as A* in NetLogo, I tried a few of different approaches, one of them was to work with the Netlogo py extention (it allows to run the Python code in NetLogo). But the thing that helped me the most was the "A General A∗ Solver in NetLogo" article [5]. It greatly helped me to understand the logic behind the implementation of algorithm in NetLogo.
File:Kulv05 astar algorithm.nlogo
Results
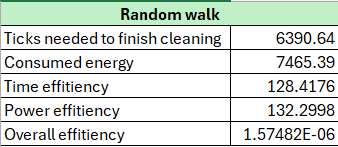
Random Walk Results
Ticks Needed for Cleaning
The algorithm requires approximately 6390.64 on average ticks to complete a cleaning cycle. This suggests that the random walk strategy leads to prolonged cleaning durations, potentially due to inefficient navigation or coverage overlap.
Energy Consumption
The robot consumes 7465.39 units of energy per cleaning task. This high energy consumption raises concerns about the sustainability of this algorithm for constant use.
Time Efficiency
The time efficiency metric of 128.4176 indicates relatively low performance concerning task completion speed. Optimized algorithms (e.g., pattern-based or path-planning algorithms) as you will soon see show better performance in this regard.
Power Efficiency
A power efficiency score of 132.2998 highlights suboptimal energy usage for task completion. This further suggests that the algorithm does not effectively balance movement and task performance relative to energy expenditure.
Overall Efficiency
The overall efficiency value of 1.57482E-06 is exceptionally low, pointing to the limited practicality of the random walk algorithm for real-world applications. This value integrates multiple performance aspects, showing the algorithm's fundamental inefficiency.
Conclusion
The random walk algorithm, while straightforward and easy to implement, demonstrates significant inefficiencies in time, energy consumption, and overall performance.
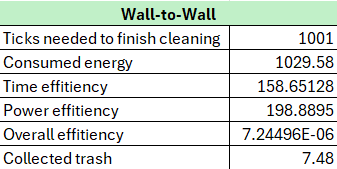
Wall-to-wall Results
Ticks Needed for Cleaning
The Zigzag algorithm requires 1001 ticks due to the settings of this particular simulation. It has a time limit to prevent it from infinitely following the walls.
Energy Consumption
Consuming 1029.58 units of energy for minimal results demonstrates inefficient energy usage. The algorithm likely spends a significant portion of this energy on unnecessary or redundant movements.
Time Efficiency
Such high value (158.65) here indicates poor efficiency in terms of time usage. The robot spends time moving inefficiently without achieving proportional cleaning results. This is because the robot spends the most of the time just walking near the wall and not collecting any trash.
Power Efficiency
This high value indicates low efficiency in utilizing energy to complete the cleaning task. The robot uses energy but achieves minimal cleaning impact. Overall Efficiency:
The value of 7.24496E-06 is too low, which highlights the algorithm’s ineffectiveness.
Trash Collection
Collecting only 7.48 units of trash, the algorithm fails to meet cleaning expectations. This suggests that the robot either covers a small area and misses significant portions of the cleaning surface.
Conclusion
The wall-to-wall algorithm is fast and relatively simple but performs poorly in terms of cleaning thoroughness and resource efficiency. This approach is best suited for scenarios where cleaning time is extremely constrained, and thoroughness is not a priority or for the cases where you just need to clean up near the walls.
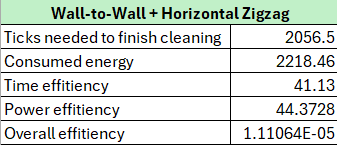
Wall-to-wall + Horizontal Zigzag Results
Time Efficiency
Wall-to-Wall + Horizontal Zigzag requires 2056.5 ticks to collect all the trash pieces. It does not have a time limit unlike the standart Wall-to-wall. The algorithm requires more than twice the time of the basic Wall-to-Wall algorithm, whish extendes the duration and allows for broader cleaning coverage and thoroughness.
Energy Consumption
The average energy needed to finish the algorithm is 2218.46 units of energy. While energy demands are higher, they are justified by the broader and more thorough cleaning achieved.
Time Efficiency
The value is 41.13. A much lower value than the first algorithm, indicating better time utilization. The robot performs more meaningful cleaning within the extended cleaning time.
Power Efficiency
The power efficiency (44.3728) is also significantly improved, showing that the energy usage aligns well with the task performed.
Overall Efficiency:
The value of 7.24496E-06 is too low, which highlights the algorithm’s ineffectiveness.
Trash Collection
The higher overall efficiency score being 1.11064E-05 indicates better optimization of resources. This value reflects a balance between energy, time, and cleaning effectiveness.
Conclusion
The Wall-to-Wall + Horizontal Zigzag algorithm provides significantly better cleaning coverage and efficiency than the first algorithm. It is ideal for scenarios where thorough cleaning is a priority, even if it requires more time and energy. This approach strikes a balance between systematic coverage and resource utilization, making it a highly effective solution for robotic vacuum cleaning.
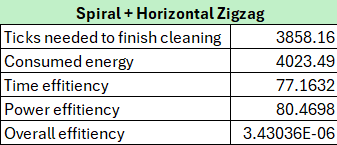
Spiral Result
Ticks Needed for Cleaning
This algorithm requires 2501 ticks due to the settings of this particular simulation. It has a time limit to prevent it from infinitely following the walls. It is higher than the ricks values the other limited time algorithms have (1001 ticks) because after the observations it takes approximately from 2200-2400 ticks for the algorithm to reach walls with this specific trajectory.
Energy Consumption
The algorithm uses 2563.74 units of energy, which is relatively high. This is due to the extended cleaning duration and the continuous movement required by the spiral pattern.
Time Efficiency
A time efficiency score of 92.97796. The time efficiency metric suggests that the algorithm does not prioritize fast cleaning. This is expected for an approach focused on systematic coverage over speed.
Power Efficiency The power efficiency value of 128.60923 is quite high, but can be seen as moderate being lower than the wall-to-wall and close enough to the random walk algorithms. This reflects that while the algorithm achieves reasonable results, it doesn’t maximize the cleaning impact per unit of energy consumed.
Overall Efficiency The overall efficiency of 4.31678E-06 is relatively low, indicating that there is room for improvement in how the algorithm balances time, energy, and cleaning performance.
Collected Trash The robot collects 27.76 units of trash, which is a not the strongest indicator of the algorithm’s effectiveness in cleaning. This average performance of trash collection value highlights its ability to remove debris across the cleaning area, but due to the trajectory it is that effective in coverage but not alcays it collecting trash.
Conclusion
The Spiral algorithm is a reliable choice for tasks that prioritize systematic coverage, but is not competitive compared to more modern and efficient cleaning strategies. Its excessive time requirements and high energy consumption make it not the greatest choice for most scenarios. While it achieves moderate trash collection, this is not enough to justify its inefficiencies.
Spiral + Horizontal Spiral Results
Zigzag Results
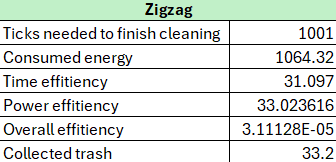
Ticks Needed for Cleaning
The Zigzag algorithm requires 1001 ticks due to the settings of this particular simulation. It has a time limit to prevent it from infinitely following the left wall.
Energy Consumption
Energy consumption of 1064.32 units is relatively moderate.
Time Efficiency
A time efficiency value of 31.097 reflects a reasonable balanced thoroughness. While not the fastest possible, the algorithm prioritizes consistent and systematic coverage. It demonstrates reasonable performance for structured cleaning.
Power Efficiency
A power efficiency score of 33.023616 highlights good energy utilization relative to task completion. This metric suggests that the Zigzag algorithm is optimized for systematic cleaning while maintaining reasonable energy demands.
Overall Efficiency
The overall efficiency value of 3.11128E-05 signifies a well-rounded performance that balances energy consumption, time management, and task effectiveness.
Collected Trash
With 33.2 units of trash collected, the Zigzag algorithm demonstrates solid cleaning effectiveness. While it is limited by not beeing the total amount of thash collected, it usually collect=st the better part of the trash, still making the room cleaner.
Conclusion
A surprising revelation was to see the algorithm collect the most part ot the trash during the trajectory run. Unlike the Wall to wall standart trajectory, the zigzag one turned out to be a good competitor. Although it still misses trash particles, it is able to go through the wast majority of the map and collect trash there (if the random placement if good enough) in 1000 ticks, something that a few other trajectories are unable to accomplish.
If we look at the definition that the robotic vacuum cleaners' algorithms do not guarantee that all room will be cleaned at the end of the cleaning, nor do they guarantee that there will be no untidy areas left within a single room, this algorithm seems to be a great option.
Overall, the Zigzag algorithm delivers reliable and effective cleaning performance and is well-suited for scenarios prioritizing thorough coverage and practical cleaning outcomes.
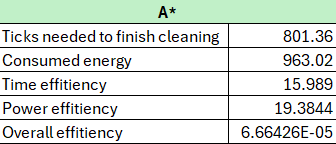
A* Results
Ticks Needed for Cleaning
The A* algorithm requires only 801.36 ticks, which is approximately 8 times fewer than the random walk algorithm (6390.64). This highlights the A* algorithm's superior path-planning capabilities, as it effectively minimizes redundant movements and optimizes navigation.
Energy Consumption
With energy consumption at 963.02 units, the A* algorithm demonstrates significantly lower energy usage than the random walk algorithm (7465.39 units). This showcases the energy-efficient nature of the A* algorithm.
Time Efficiency
The time efficiency metric of 15.989 is substantially better compared to the random walk's 128.4176, suggesting that the A* algorithm is far more time-efficient in completing cleaning tasks.
Power Efficiency
A power efficiency score of 19.3844 indicates much better energy management compared to the random walk algorithm (132.2998). This implies that the A* algorithm optimizes the robot's movement to minimize energy waste.
Overall Efficiency
The overall efficiency value of 6.66426E-05 is significantly higher than the random walk algorithm's 1.57482E-06, highlighting the A* algorithm's substantial improvements in task performance across all key metrics.
Conclusion
The A* algorithm outperforms the random walk algorithm across all key metrics, providing significantly better cleaning efficiency, lower energy consumption, and improved time management. Its implementation is highly recommended for robotic vacuum systems where performance and energy savings are priorities.
Conclusion
Citations
[1]https://www.diva-portal.org/smash/get/diva2:1213349/FULLTEXT02.pdf
[2] https://ouster.com/insights/blog/introduction-to-slam-simultaneous-localization-and-mapping
[3] https://www.geeksforgeeks.org/a-search-algorithm/
[4] https://www.diva-portal.org/smash/get/diva2:1213970/FULLTEXT02.pdf
[5] https://www.cs.us.es/~fsancho/Blog/posts/General_A_Solver_NetLogo.md.html#a*forpathfindingin2dgrids
Code
File:Kulv05 randomwalk algorithm.nlogo
File:Kulv05 standart walltowall algorithm.nlogo
File:Kulv05 walltowall horiz zigzag algorithm.nlogo
File:Kulv05 standartspiral algorithm.nlogo
File:Kulv05 spiral horiz zigzag algorithm.nlogo