Simulace přestupu stanice metra Můstek

Mezi nejrušnější stanice pražského metra patří stanice Můstek, dle statistiky [TODO: citace]. Tato stanice je navíc přestupní z linky A na linku B a i pro mnohé Pražáky může díky své komplexitě působit jako labyrint. Proto mnohdy, když spěcháte na Můstku v nejrušnější hodiny na navazující spoj, je klíčové zvolit si správnou trasu přestupu.

Definice problému

Cílem této simulace je zjistit, která trasa je při přestupu z linky A na linku B a naopak nejlepší v období nejrušnějších hodin. Zprvu může tento problém působit jako problém nalezení nejkratší cesty, v takovém případě bychom ale neuvažovali vytíženost metra, tedy počet lidí, kteří se metrem pohybují.

Metoda

Simulace byla provedena v prostředí NetLogo. Byl vytvořen model stanice metra a cestujících, kteří přestupují z linky A na linku B. Simulace pro zjednodušení nezohledňuje pohyb lidí, kteří do metra vstupují nebo z něj vystupují. Nezohledňuje také nelogické cesty, tedy takové cesty, které nevedou k přestupu z jedné linky na druhou případně jsou neoptimální.

Simulace byla provedena ve dvou nejrušnějších hodinách pracovního dne.

Model

Data

Nejvytíženější hodiny

Pro získání statistiky o zátěži metra bylo využito statistiky [TODO: citace] z roku 2015. Ze statistiky vyplývá, že nejrušnější hodiny v pracovním dny jsou 7-8 a 17-18. Je potřeba podotknout, že časy v okolí těchto hodin jsou z pohledu vytíženosti dosti podobné. Tyto dva časy jsem zvolil, protože se v nich nachází špička vytížení. Data o časech příjezdu metra byla pak převzata z jízdních řádů PID [TODO: citace].

Počet cestujících

Dalším údajem, který bylo potřeba získat, je počet lidí, kteří přijíždějí a přestupují z linky A na linku B a naopak. K tomu jsem opět využil statistiky, tentokrát o přestupech [TODO: citace] z roku 2015.

Pro každou linku a čas příjezdu je potřeba získat údaj o počtu cestujících, kteří ze soupravy metra vystoupí. Nabízí se jednoduché řešení: generovat počet cestujících pomocí normálního rozdělení. Tato metoda je vhodná, protože mnoho přírodních a lidských jevů, včetně pohybu cestujících, se přibližně řídí normálním rozdělením. Navíc, díky Centrální limitní větě, i když jednotlivé příjezdy nejsou normálně rozdělené, jejich součet za určité období se normálnímu rozdělení přibližuje.

Vzhledem, k datům které mam dostupné nebudu bohužel moc jednoduše dopočítat průměr a směrodatnou odchylku jelikož o přestupech v daných časech. Ze statistiky jsem schopen dopočítat pouze:

• Průměr a směrodatnou odchylku pro počet přestupy B-A cestujících z přijíždějícího metra v čase 7-8 - μ = 118, σ = 12
• Průměr a směrodatnou odchylku pro počet přestupy A-B cestujících z přijíždějícího metra v čase 17-18 - μ = 128, σ = 6

Jak je vidět chybí mi průměr a směrodatné odchylky:

• B-A v čase 17-18
• A-B v čase 7-8

Pro jejich určení využijeme vztahu mezi A-B a B-A přestupech v časech 7-8 a 17-18. Ve statistice si můžeme povšimnout, následujícího vztahu:

• B-A v čase 17-18 je přibližně 4149 přestupů
• A-B v čase 17-18 je přibližně 3609 přestupů
• B-A v čase 7-8 je přibližně 3395 přestupů
• A-B v čase 7-8 je přibližně 4633 přestupů

Je to zcela logické protože se lidé co přestupovali ráno vracejí zpět domů. Můžeme tedy údaje pro A-B v čase 17-18 použít pro normální rozdělení B-A v čase 7-8 a údaje pro A-B v čase 7-8 použít pro normální rozdělení B-A v čase 17-18.

Agenti - Cestující

V simulaci mají cestující za cíl dojít k náhodně zvolenému přestupu nebo také východu.

'Příjezd' cestujících

Vlaky s cestujícími přijíždějí dle jízdního řádu kde se 100 ticku v simulaci bere jako jedna minuta. Jejich počet je určen normálním rozdělením viz. předchozí část, a jsou náhodně rozmístěni po soupravě. Při jejich příjezdu je jim náhodně nastavena jejich rychlost pohybu, barva, velikost, ttl a jiné pomocné proměnné.

Parametry cestujících

• pace - rychlost pohybu určená random normal 1 0.2 (Převzato z ukázkového příkladu na braného v rámci předmětu.)
• current-step - aktuální fáze pohybu ve které se cestující nachází
• arriving-in-train - index koleje ze, které cestující startuje
• transfer-exit - náhodně vybraný výstup v přestupní chodbě
• transfer-exit-steps - náhodně vybraná cesta k přestupu
• current-transfer-exit-step - aktuální krok v cestě z předchozího bodu
• ttl - počet ticku po kterém se neaktivní cestující vymažou
• path - pro uložení cesty kterou cestující urazil
• path-distance - pro uložení vzdálenosti, kterou cestující urazil
• Umístění cestujících v soupravě - náhodně se vybere souřadnice x a y z vymezeného intervalu soupravy.

Pohyb

Simulace pohybu cestujících zahrnuje několik klíčových fází, které umožňují realistické modelování chování cestujících. Každá fáze má své specifické úkoly a postupy, které zajišťují, že se cestující pohybují plynule a přirozeně:

1. exit-train - Cestující ve vlaku najde nejbližší souřadnice platformy nástupiště a dojde tam. Po dokončení fáze se fáze pohybu změní na go-to-nearest-platform-exit.
2. go-to-nearest-platform-exit - Na základě aktuální pozice na nástupišti cestující vyhledá nejbližší přestupní chodbu a vydá se k ní. Po dokončení fáze se fáze pohybu změní na enter-transfer-tunels.
3. enter-transfer-tunels - Po tom co cestující dorazí k přestupní chodbě bude přenesen do chodby a bude mu náhodně vybrán jeden z možných východu a cesta k němu, které se nastaví do transfer-exit a transfer-exit-steps. Cesta je určená pomocí listu souřadnic a aby pohyb cestujících působil méně staticky jsou tyto souřadnice určeny náhodně z intervalu. Po dokončení fáze se fáze pohybu změní na exit-transfer-tunels.
4. exit-transfer-tunels - Cestující postupně jde zadanou cestou z transfer-exit-steps. Pokud cestující prošel všemi body cesty pokusí se nejkratší cestou dojit k transfer-exit. Pokud dojde k transfer-exit porovná vzdálenost, kterou urazil v parametru path-distance s nejlepší nalezenou vzdálenosti od soupravy k východu a nastaví ji jako nejlepší pokud je kratší. Následně se vymaže se.

Na následujících obrázcích můžete vidět všechny trasy definované v přestupových chodbách, ze kterých se náhodně vybírá. Vybíral jsem pouze logické cesty.

V jednotlivých bodech abstraktně zmiňuji "dojde tam" a "vydá se k ní", ve skutečnosti mi z celé práce nejvíce dalo zabrat správné nastavení pohybu. Prostor metra, jak je vidět v sekci prostředí, není úplně triviální. Ve zkratce, pohyb funguje tak, že se nejdříve otočí směrem k vybranému cíli, následně se pohyb provede, pokud je to možné. Aby se pohyb provedl, musí se zabránit srážce s ostatními cestujícími a nárazu do překážek.

Pro zabránění srážkám cestujících se vzájemně, cestující se před každým krokem podívá před sebe. Pokud zjistí, že je na daném místě jiný cestující, otočí se náhodně o 0 až 180 stupňů.

Dalším problémem jsou překážky, kterým by se cestující měli vyhnout. Pokud cestující narazí na zeď, zkontroluje své sousedy(okolní patche) a vybere souseda, který není zdí a je nejblíže k cíli. Abychom předešli zasekávání, náhodně otočíme cestujícího o 0 až 45 stupňů ve 20 % případů. Tento systém vyhýbání se však nemusí vždy dokonale dařit. Proto má každý cestující parametr ttl nastavený na 50, ze kterého odečítáme, pokud se cestující nepohne, a nastavujeme ttl na 50, pokud k pohybu došlo. Pokud ttl klesne na 0, označíme cestujícího za ztraceného a odstraníme ho ze simulace.

Prostředí - Metro

Tvorba mapy metra

Vzhledem ke složitosti metra jsem se rozhodl vytvořit jeho mapu pomocí pixel artu a následně ji do NetLoga importovat pomocí import-pcolors. Pixel art mapu s názvem "metro.png" naleznete v příloze společně s kódem a je potřeba k jeho fungování stejně tak jako "metro-layout.png" sloužící k popisu mapy pomocí import-drawing. Veškeré kreslení jsem vytvářel pomocí nástroje Piskel a mohu ho vřele doporučit.

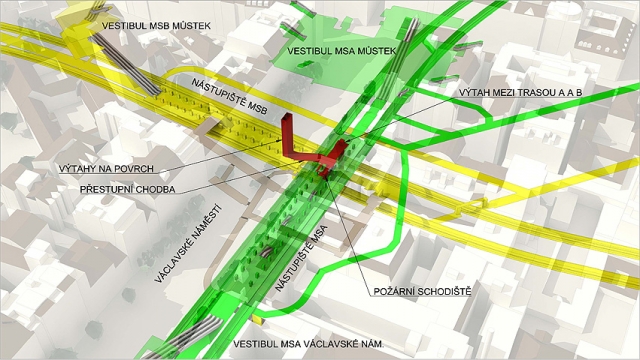
Při tvorbě mapy jsem si naivně myslel, že narazím na plánek metra s popisem přestupů, ale i při usilovném hledání jsem na nic takového nenarazil. Našel jsem ale pár dobových fotografií, které můžete dále vidět níže a podle kterých jsem mapu vytvářel. Po jejím vytvoření jsem se rozhodl stanici metra navštívit, abych zjistil, jak přesně metro vypadá a zda mnou vytvořená mapa odpovídá realitě.

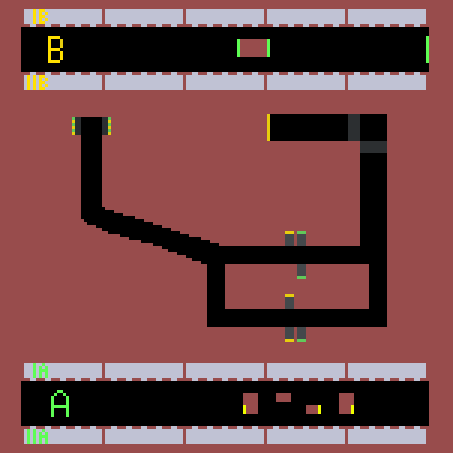
Na následujícím obrázku je výsledná mapa metra.

Speciální prvky

Mapa obsahuje i "Speciální prvky", které mají vliv na agenty. Jedná se o schody, které jsem označil barvou pcolor 2.5, ty zpomalují rychlost agenta o polovinu, a eskalátory označené barvou pcolor 1.6, ty dávají agentovi konstantní rychlost 1.

Zobrazení nejlepší cesty

Jak již zaznělo v zadání, cílem je zjistit nejkratší cestu od vlaku až k přestupu. Pro tento účel jsem se rozhodl zobrazovat nejlepší cestu přímo do mapy. Jednoduše se zvolí, jakou kolej chcete zkoumat, zadáte "zobrazit nejlepší přestup" a zobrazí se nejlepší nalezený přestup vyznačený červenou barvou, viz ukázka níže. Jak jsem již uváděl, nejlepší přestup se získá v poslední fázi porovnáním dosavad získaného nejlepšího přestupu s přestupem, který cestující provedl.

Nastavení metra

V simulaci se dá nastavit, jestli se má použít jízdní řád 7-8 nebo 17-18. Dalším ovládacím prvkem je frekvence přijezdu, která umožní změnit intervalu mezi příjezdy vlaků (mění se počet ticků které be berou jako jedna minuta). Defaultně je tato hodnota nastavena na 100.

Problémy modelu

1. Asi největší problém plyne už ze samotného zadání. Zkoumám tady nejkratší cestu na tu, ale agenti nemají moc vliv. Místo toho jsem se měl spíše věnovat zkoumáním zátěže metra.
2. Krom toho vidim problém i v použitém data setu který není úplný.
3. Pohyb cestujících není optimální a celková neúplnost modelu výsledky zkresluje.

Výsledky

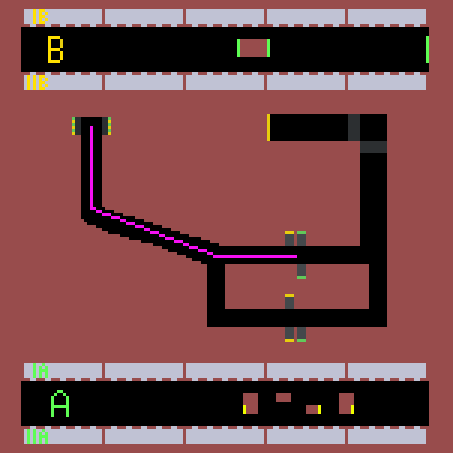
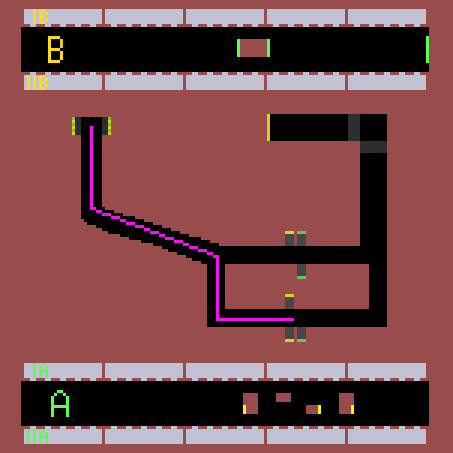
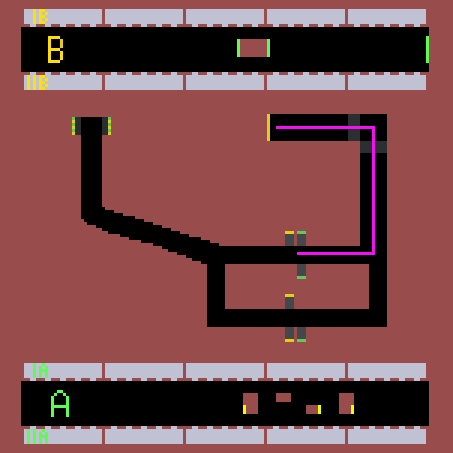
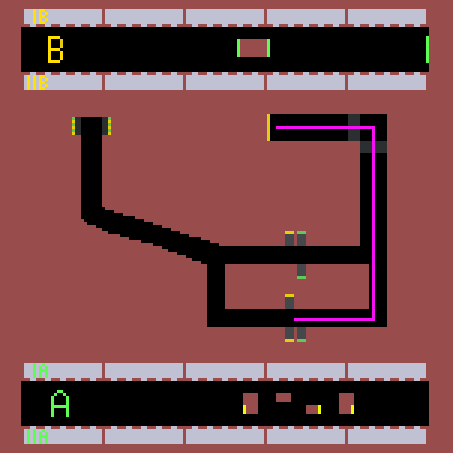
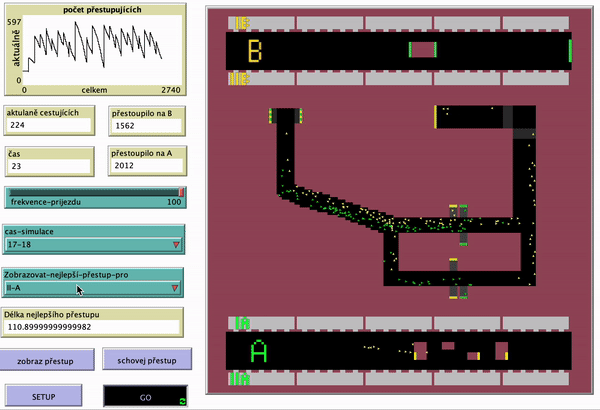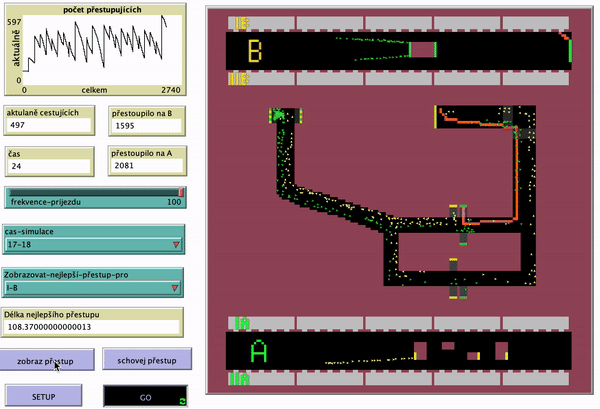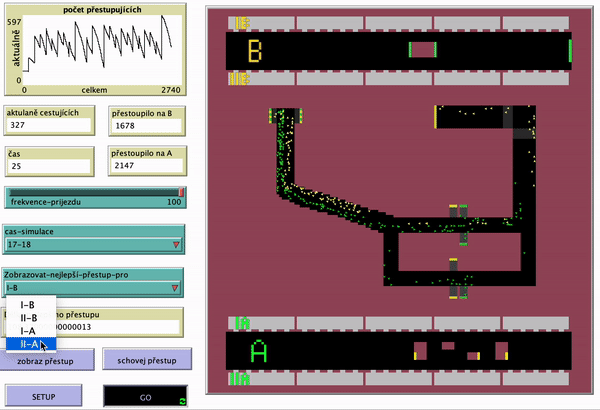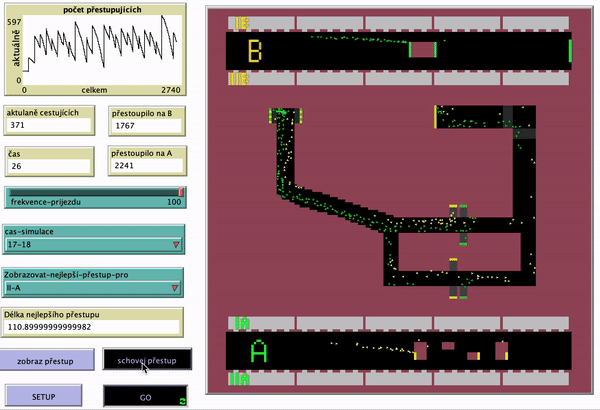
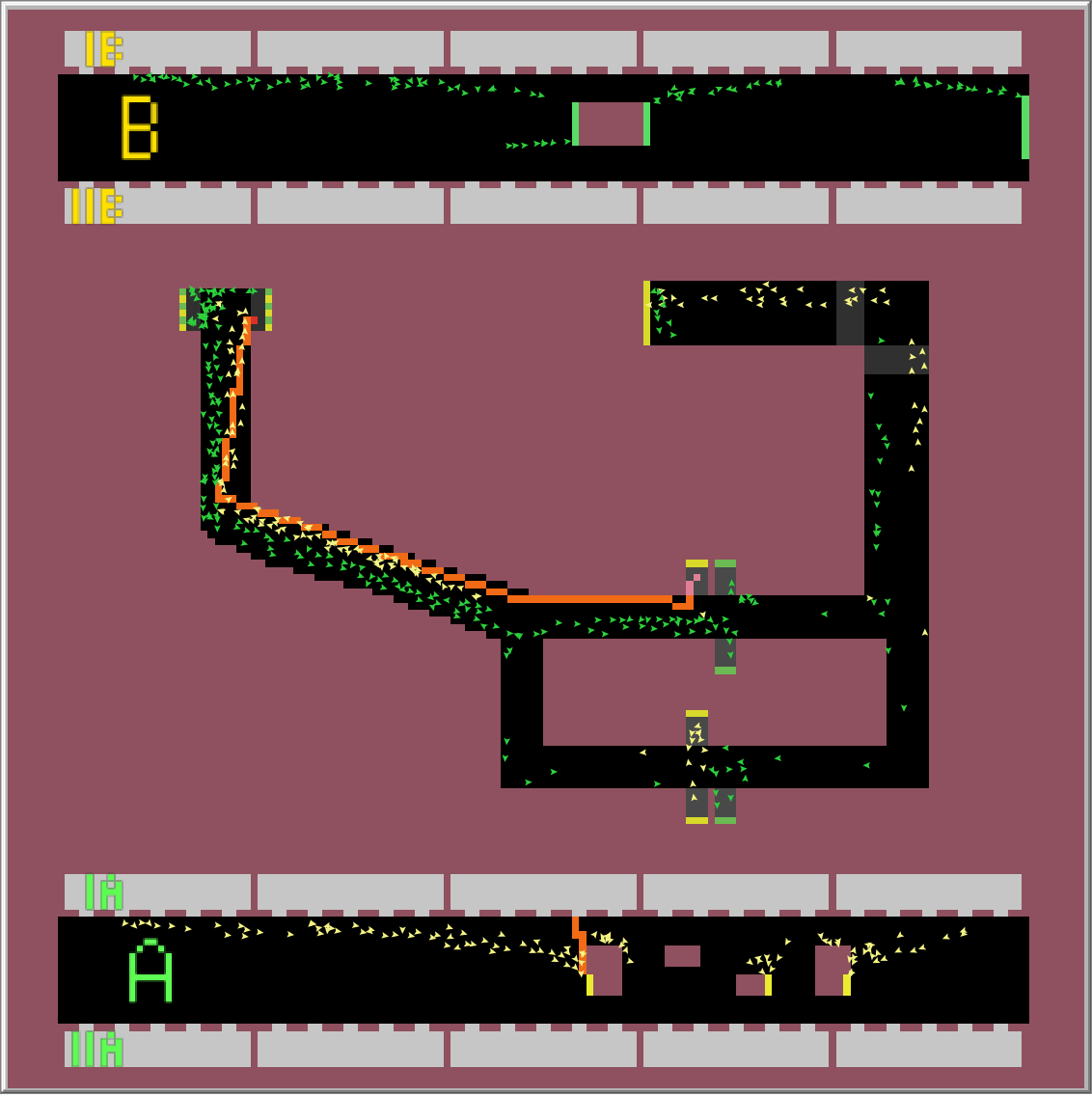
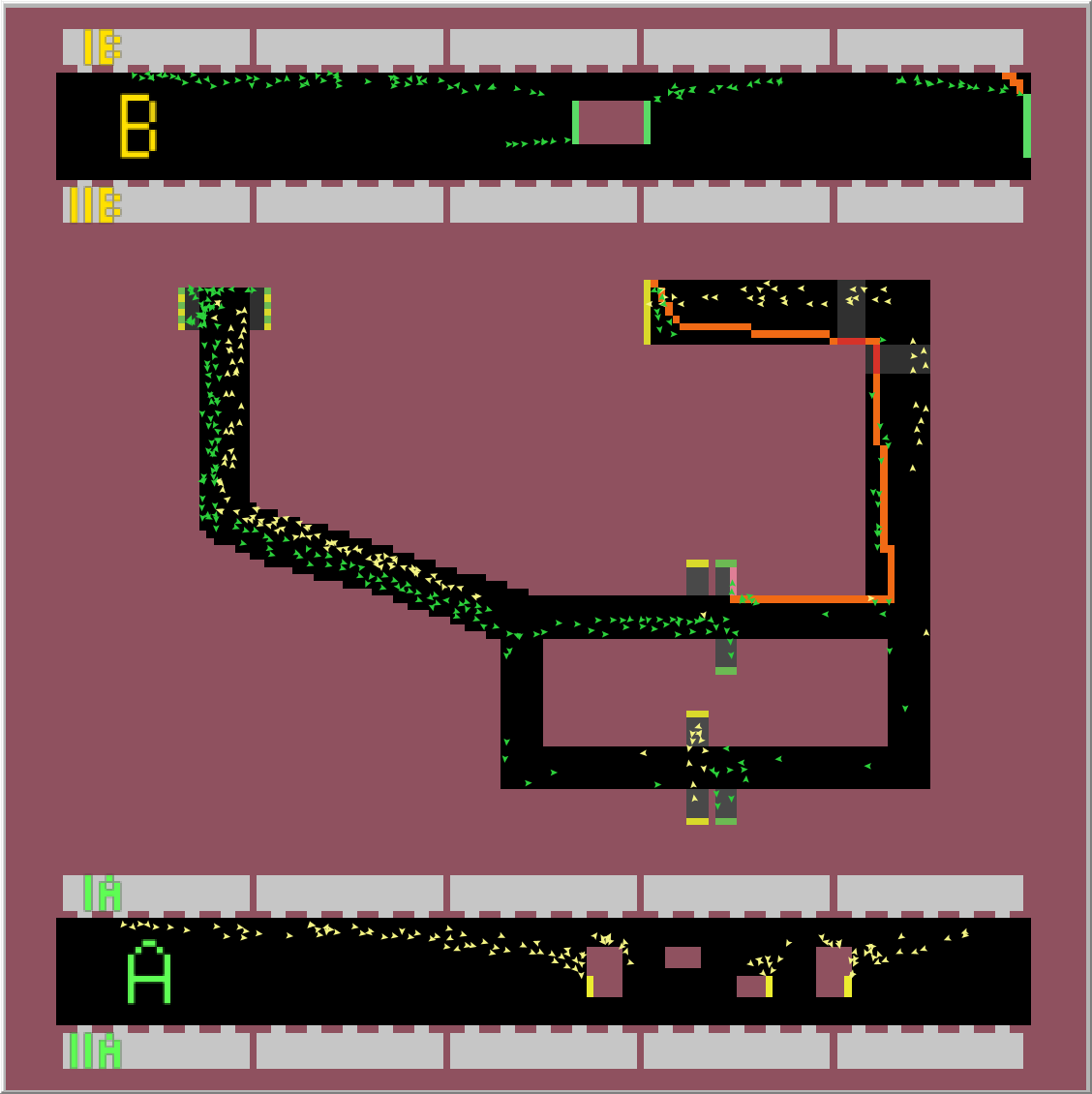
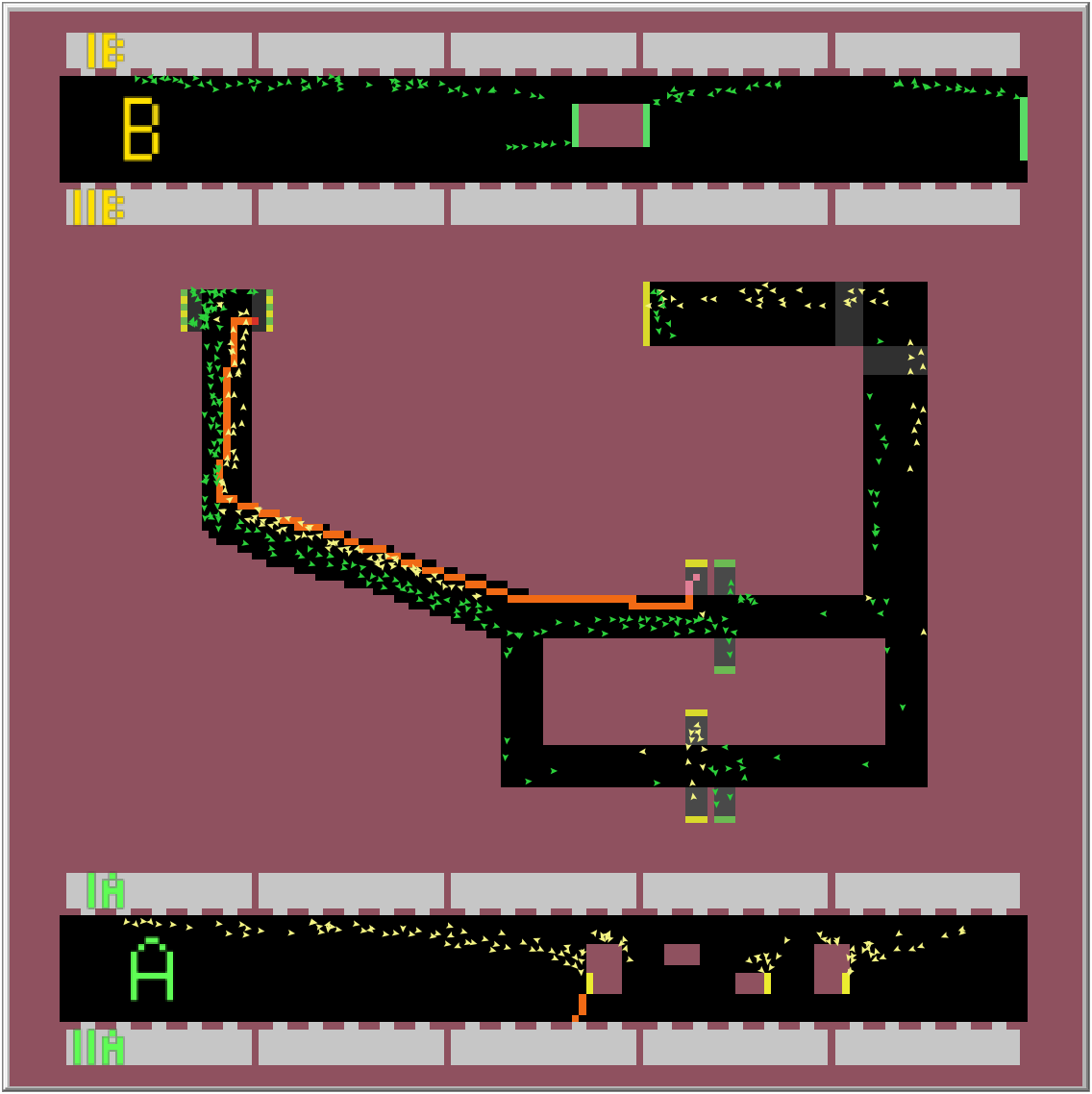
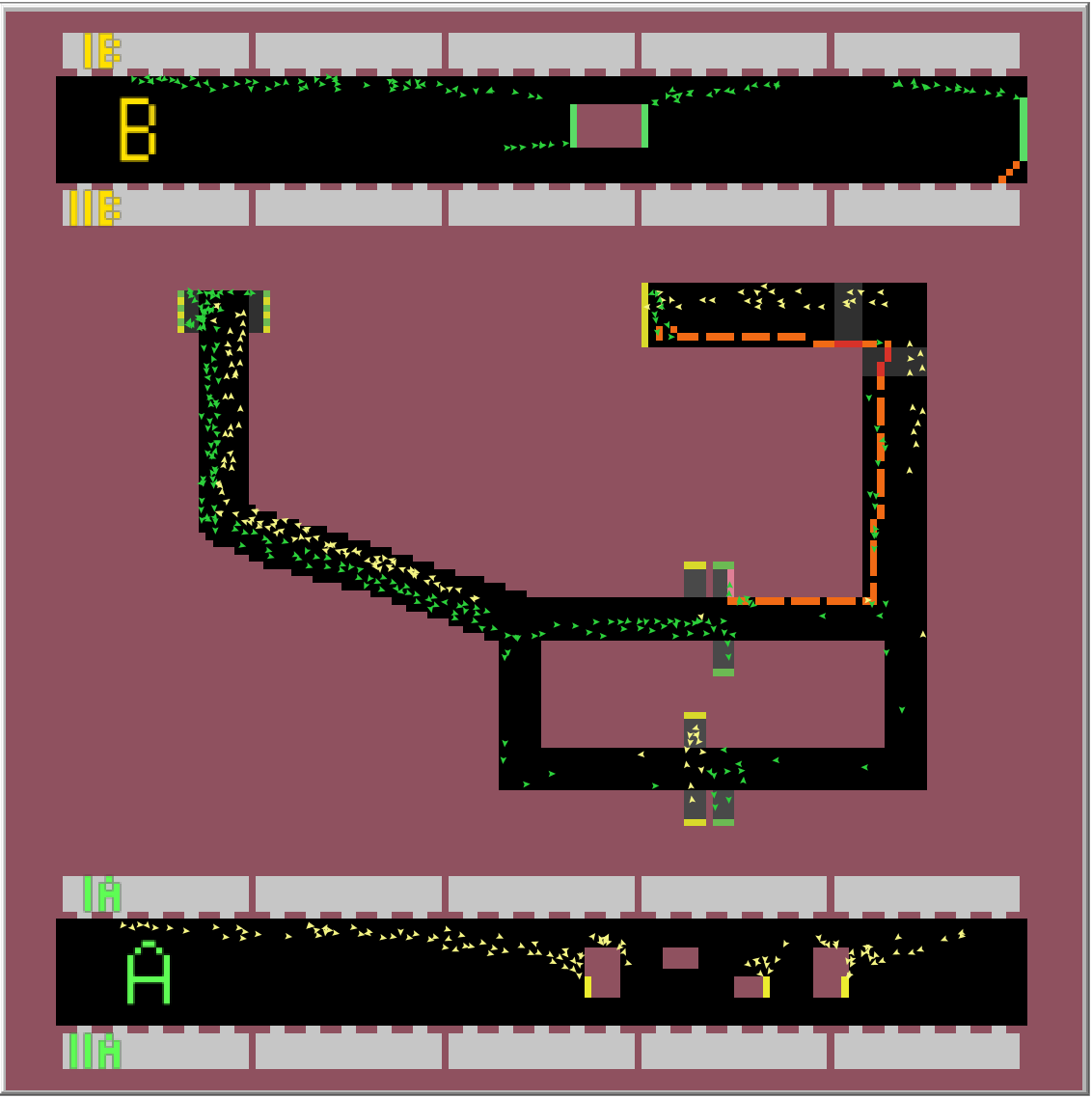
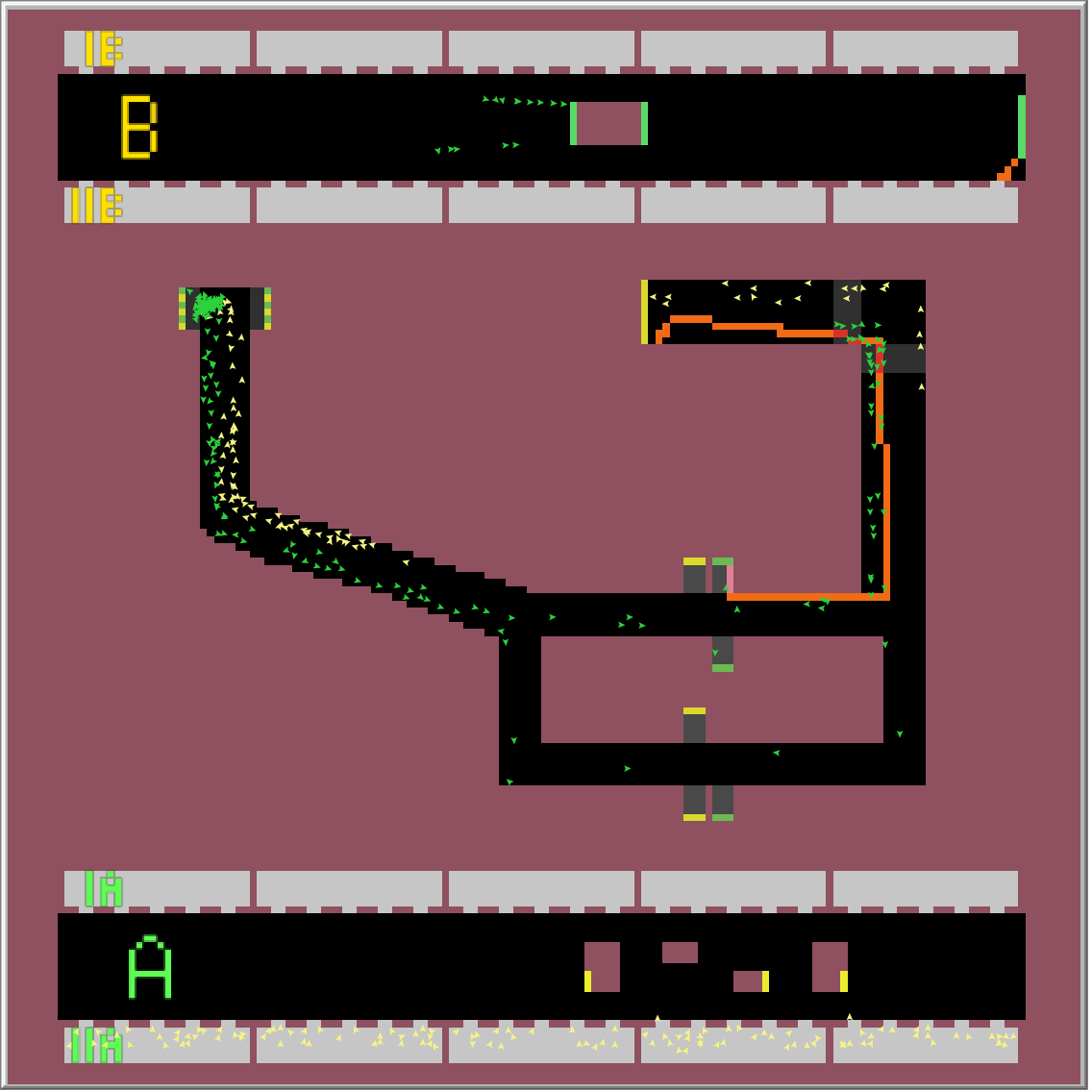
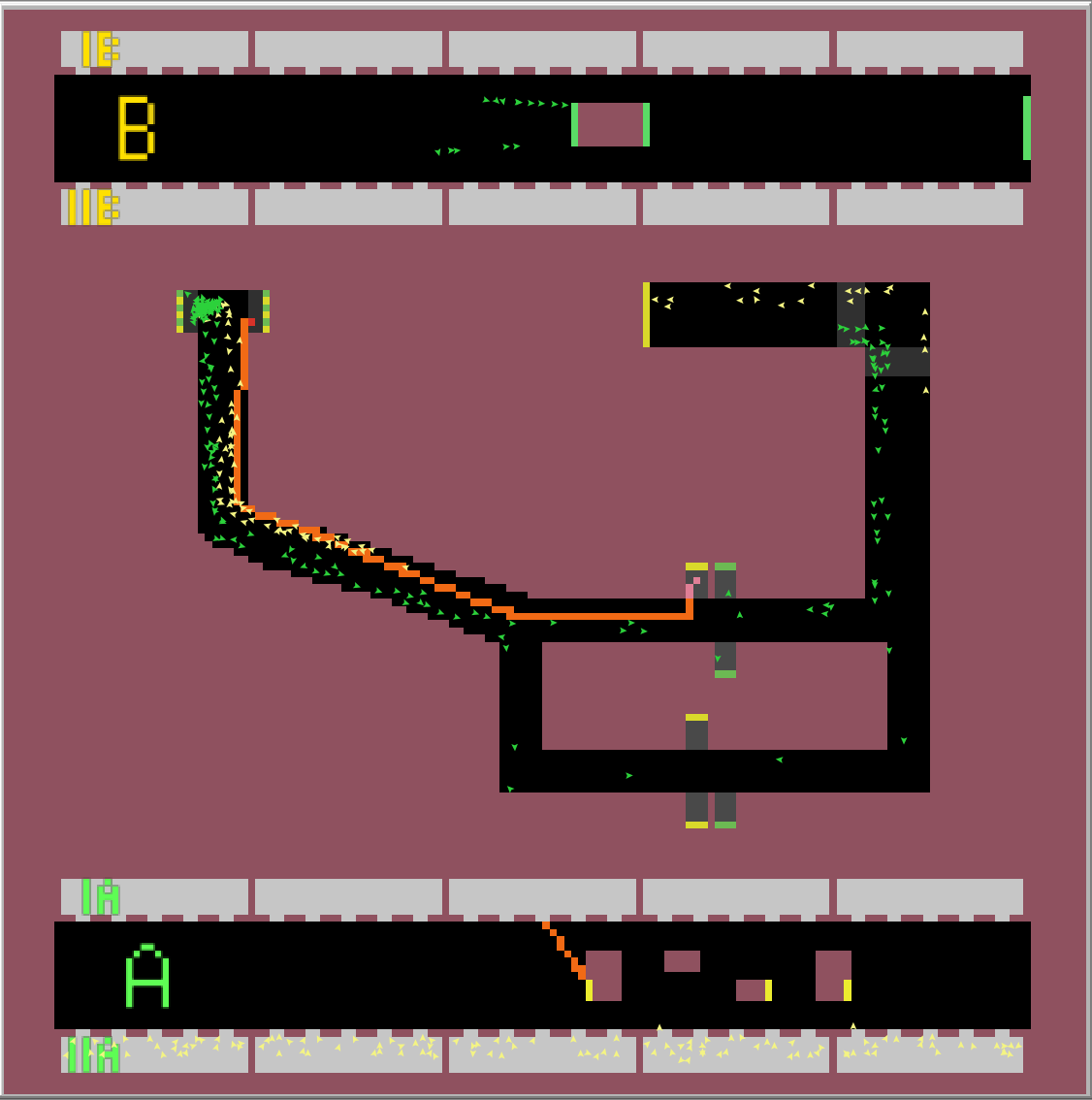
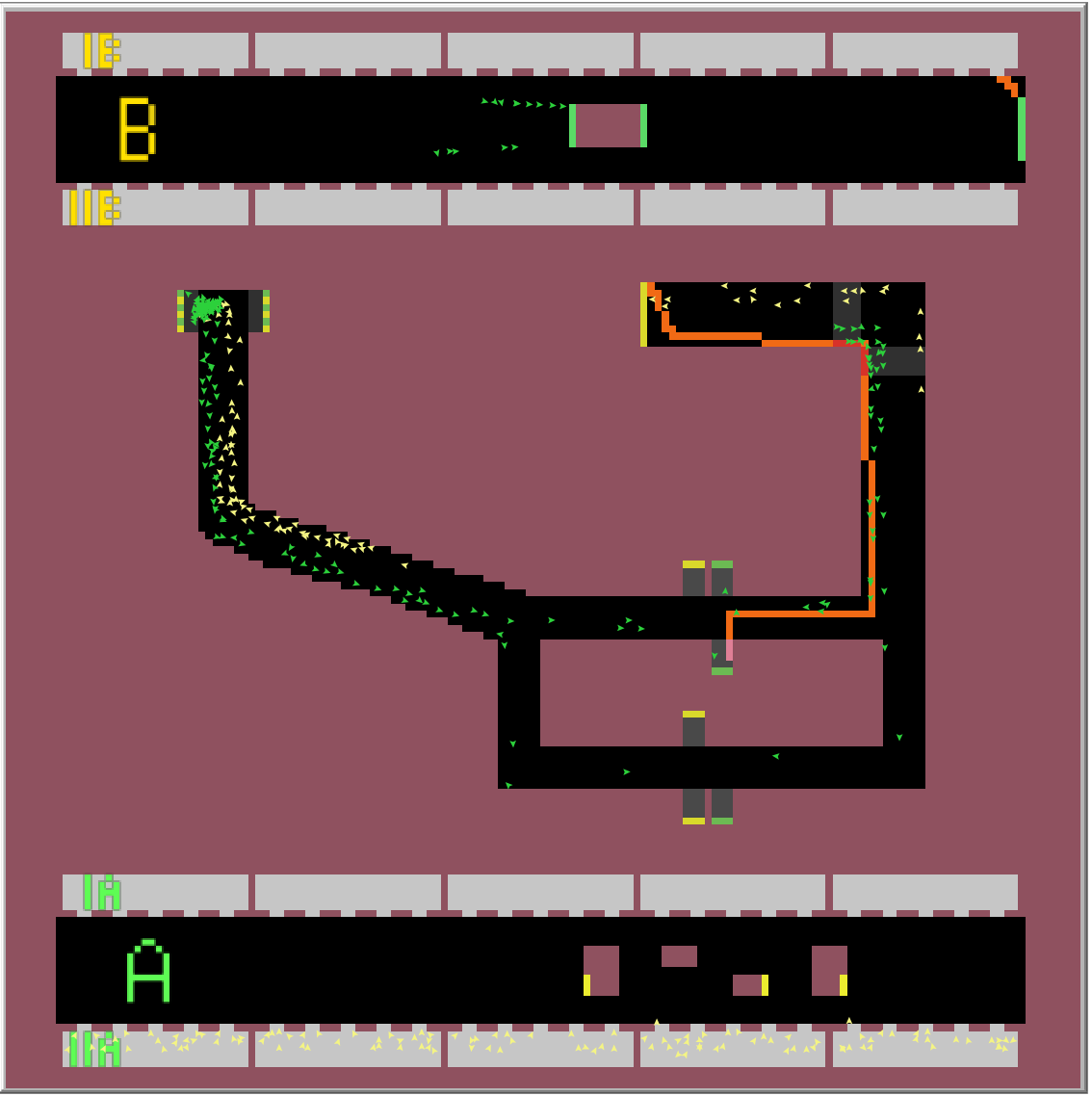
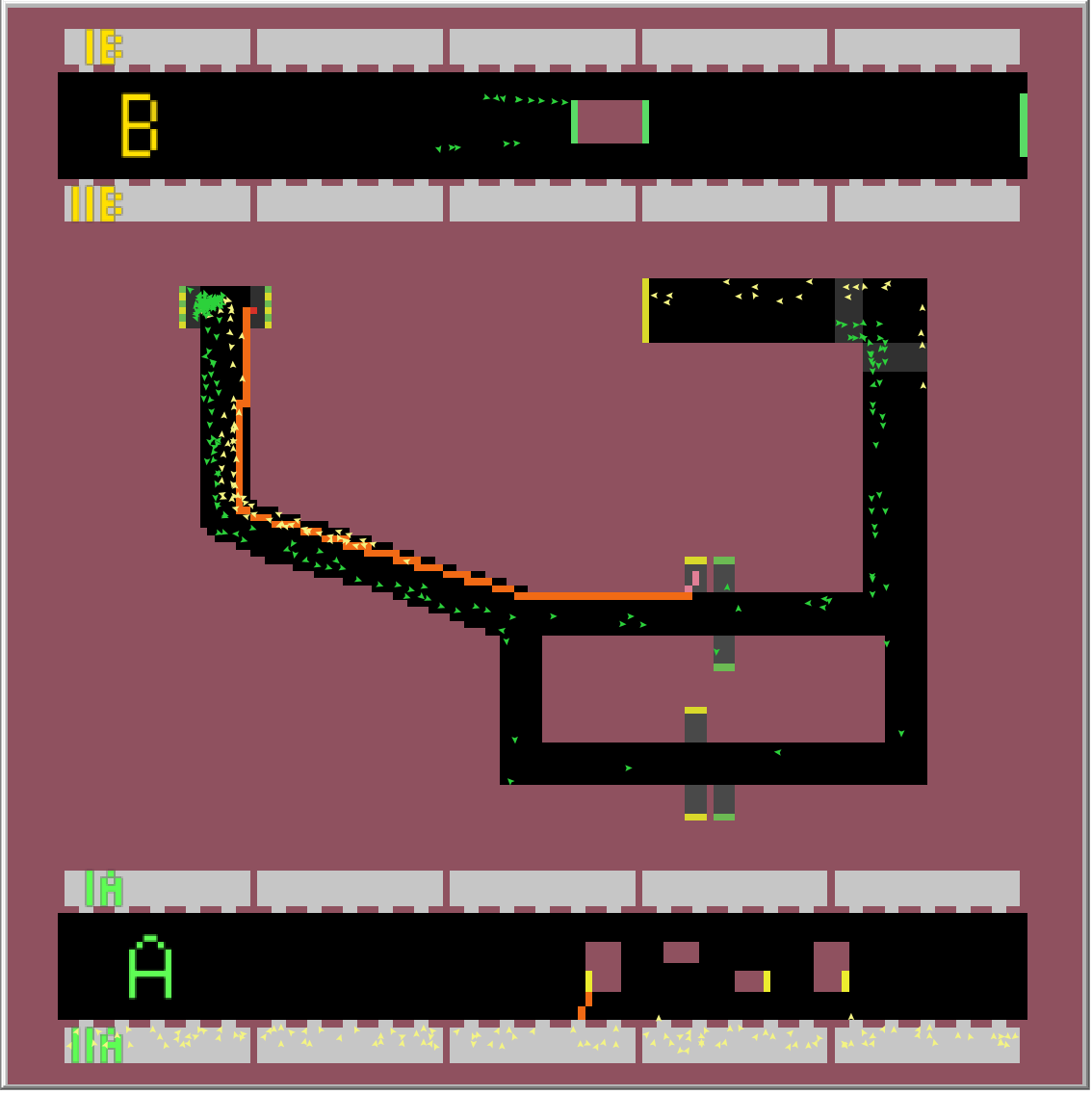
Výsledkem simulace je nalezení nejkratší cesty pro vlaky z obou směrů obou linek. Simulaci jsem prováděl 1 hodinu odsimulovaného času (6000 ticku) pro každý časový úsek. Jak je vidět z linky B, je lepší být v posledním nebo prvním vagonu soupravy, jít přestupem, který je nejblíž, a následně zabočit doprava při první možnosti. U linky A je zase nejlepší být v prostředních vagonech a následně přestoupit skrze eskalátor nejvíc vlevo a vydat se směrem doleva. Na výsledky přitom neměl časový úsek žádný vliv. Na následujících obrázcích můžete vidět nejlepší nalezené přestupy.

Úsek 7-8

Úsek 17-18

Je nutné podotknout, že tyto výsledky jsou pouze orientační, vzhledem k nepřesnostem ve vytvořené mapě (není 1:1). Vliv agentů na nalezení nejkratší trasy je minimální. Simulace by v budoucnu mohla být vylepšena o počet srážek s agenty, což by se zohlednilo při hledání nejlepší trasy (delší trasy by tak mohly být lepší než kratší).

Závěr

Úspěšně se mi podařilo nalézt nejkratší trasy pomocí simulace. Výsledné trasy jsem na vlastní kůži vyzkoušel a na první pohled se zdají být skutečně nejkratší (měřil jsem krokoměrem). I přes tyto úspěchy bych rád podotknul, že zvolený cíl simulace, který se mi na začátku zdál vhodný pro agentní simulaci, se v průběhu ukázal jako celkem nevhodný jelikož agenti neměli vliv na nalezenou cestu. Pro simulaci na dané téma by se spíše hodil cíl jako "simulovat zatížení metra v dopravní špičce" a taky data, která se na první pohled zdála jako zdánlivě perfektní, neobsahovala dostatek informací.