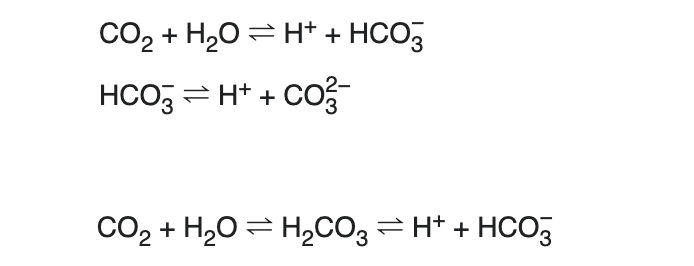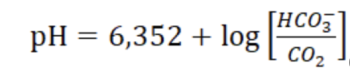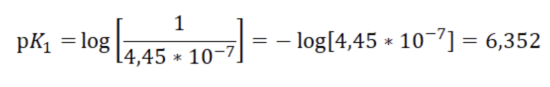Difference between revisions of "Simulation of the Ocean Carbon Uptake"
(→Variables) |
(→Method) |
||
| Line 21: | Line 21: | ||
=Method= | =Method= | ||
| + | A Bjerrum plot illustrates the concentrations of various species of a polyprotic acid in a solution at equilibrium, plotted against the pH of the solution. Given the broad range of concentrations spanning multiple orders of magnitude, it is customary to represent them on a logarithmic scale. In certain instances, the plot may depict ratios of concentrations instead of their absolute values. Occasionally, the concentrations of H+ and OH− ions are also included in the plot. | ||
| + | |||
| + | [[File:Bjerrum_plot.png|thumb|center|850px|Example Bjerrum plot: Change in carbonate system of seawater from ocean acidification.]] | ||
| + | |||
| + | Suppose that the reactions between carbon dioxide, hydrogen ions, bicarbonate and carbonate ions, all dissolved in water, are as follows: | ||
| + | |||
| + | [[File:Co2_formula.png]] | ||
| + | |||
| + | An increase in the concentration of carbon dioxide in water leads to a decrease in the proportion of carbon dioxide that reacts with water to form carbonic acid. But due to the general increase in the concentration of carbon dioxide in water, the pH of such water will decrease to a value of 4.0. Below this value, carbon dioxide is practically insoluble in water. | ||
| + | |||
| + | Consider an example in which water containing carbon dioxide also contains sodium bicarbonate (NaHCO3). In this case, calculation of the pH value is possible using equation. | ||
| + | |||
| + | The water contains the following concentrations of carbon dioxide and sodium bicarbonate: | ||
| + | |||
| + | [[File:PH_formula.png|350px|]] | ||
| + | |||
| + | Here it is necessary to clarify how the record form for the request was obtained. The dissociation constant or equilibrium constant of the equation for the dissolution of carbon dioxide in water at the first stage is equal to K1 = 4.45 * 10-7. The equilibrium (dissociation) constant of a given medical regimen can be written as: | ||
| + | |||
| + | [[File:Dissociation_constant.png|550px|]] | ||
| + | |||
=Variables= | =Variables= | ||
The model setup: | The model setup: | ||
Revision as of 01:32, 21 January 2024
Name: Simulation of the Ocean Carbon Uptake
Author: Aiyyna Tatarinova
Method: System dynamic
Tool: Vensim
Contents
Introduction and Problem definition
Carbon dioxide (CO2) is a crucial greenhouse gas responsible for trapping heat. It originates from the extraction and combustion of fossil fuels (such as coal, oil, and natural gas), wildfires, and natural phenomena like volcanic eruptions. The initial chart displays the levels of atmospheric carbon dioxide (CO2) recorded by NOAA at the Mauna Loa Observatory in Hawaii since 1958.
Since the advent of industrialization in the 18th century, human activities have elevated atmospheric CO2 levels by 50%, resulting in the current amount being 150% of its value in 1750. This anthropogenic increase surpasses the naturally occurring rise observed at the conclusion of the last ice age 20,000 years ago. Carbon is in carbon dioxide, which is a greenhouse gas that traps heat close to Earth. It helps Earth hold some of the heat it receives from the Sun so it doesn't all escape back into space. But CO2 is only good up to a point – beyond that point, Earth's temperature warms up too much. NASA research satellites such as OCO-2 and OCO-3 are studying how carbon moves around the planet.
The ocean holds approximately sixty times more carbon in the form of dissolved inorganic carbon than the pre-anthropogenic atmosphere (~600 Pg C). Over time scales <105 years, the ocean serves as the largest reservoir of inorganic carbon (~38,000 Pg C), engaging in exchanges with atmospheric carbon dioxide (CO2) and thus exerting significant control over atmospheric CO2 levels. The average concentration of inorganic carbon in the ocean is approximately ~2.3 mmol kg−1, with a residence time of about ~200 thousand years.
Dissolved carbon dioxide in the ocean primarily exists in three inorganic forms: free aqueous carbon dioxide (CO2(aq)), bicarbonate (HCO3−), and carbonate ion (CO32−). A minor presence is true carbonic acid (H2CO3), accounting for less than 0.3% of [CO2(aq)]. The combined concentrations of [CO2(aq)] and [H2CO3] are represented as [CO2].The predominant form of dissolved inorganic carbon in the contemporary ocean is bicarbonate (HCO3−), comprising over 85% of the total.
Carbon dioxide undergoes exchange between the atmosphere and the ocean through molecular diffusion. A disparity in CO2 pressure between the atmosphere and the ocean drives the exchange of CO2. Specifically, CO2 transfers from the air to the water when the atmospheric CO2 pressure is higher. The ocean dissolves CO2 due to its solubility.
The solubility of carbon dioxide is influenced by the water's salinity and temperature, with a limited capacity for absorption by the water. Colder water has a higher capacity to dissolve CO2, contributing to variations in solubility.
Method
A Bjerrum plot illustrates the concentrations of various species of a polyprotic acid in a solution at equilibrium, plotted against the pH of the solution. Given the broad range of concentrations spanning multiple orders of magnitude, it is customary to represent them on a logarithmic scale. In certain instances, the plot may depict ratios of concentrations instead of their absolute values. Occasionally, the concentrations of H+ and OH− ions are also included in the plot.
Suppose that the reactions between carbon dioxide, hydrogen ions, bicarbonate and carbonate ions, all dissolved in water, are as follows:
An increase in the concentration of carbon dioxide in water leads to a decrease in the proportion of carbon dioxide that reacts with water to form carbonic acid. But due to the general increase in the concentration of carbon dioxide in water, the pH of such water will decrease to a value of 4.0. Below this value, carbon dioxide is practically insoluble in water.
Consider an example in which water containing carbon dioxide also contains sodium bicarbonate (NaHCO3). In this case, calculation of the pH value is possible using equation.
The water contains the following concentrations of carbon dioxide and sodium bicarbonate:
Here it is necessary to clarify how the record form for the request was obtained. The dissociation constant or equilibrium constant of the equation for the dissolution of carbon dioxide in water at the first stage is equal to K1 = 4.45 * 10-7. The equilibrium (dissociation) constant of a given medical regimen can be written as:
Variables
The model setup: • Units for Time = Year
• INITIAL TIME = 0
• FINAL TIME = 250
• TIME STEP = 1
The model variables are set as follows:
• Dissociation constant = 6.352
• Bicarbonate = Dissolved carbon dioxide in the ocean/100*98 = Dissolved carbon dioxide in the ocean / 100 * 98
• Bicarbonate HCO3 concentration = Bicarbonate*0.001/Molar mass HCO3
• Bicarbonate HCO3 concentration in mol/l = Bicarbonate HCO3 concentration*1000
• Carbon dioxide = Dissolved carbon dioxide in the ocean/100*2
• Carbon dioxide concentration = Carbon dioxide*0.001/Molar mass CO2
• Carbon dioxide concentration in mol/l = Carbon dioxide concentration*1000
• pH value = Dissociation constant+LOG("Bicarbonate HCO3 concentration in mol/l"/"Carbon dioxide concentration in mol/l", 10)
• Molar mass HCO3 = 61
• Molar mass CO2 = 44
• Dissolved carbon dioxide in the ocean = Atmosphere/100*30
• Atmosphere = INTEG (CO2 emissions+CO2 release+decomposition+respiration-CO2 absorption-photosynthesis,898.86)
• ocean mixing = 100*(Deep Ocean/38100)
• Ocean surface = INTEG ( CO2 absorption+ocean mixing-remains-CO2 release, 1020)
• Deep Ocean = INTEG ( remains-ocean mixing, 38100)
• photosynthesis = 121.8*(Atmosphere/750)
• Forest = INTEG ( photosynthesis-death-respiration, 610)
• death = 60 * (Forest/610)
• CO2 emissions = 5.5
• Fuel = INTEG ( -CO2 emissions, 10000)
• remains = 91.6 * (Ocean surface/1020)
• CO2 absorption = 92 * (Atmosphere/750)
• CO2 release = 90* (Ocean surface/1020)
• decomposition = 60 * (Soils/1580)
• respiration = 61.6 * (Forest/610)
• Soils = INTEG ( death-decomposition, 1580)
Model
The diagram of carbon dioxide shows exchange in the atmosphere and its impact on ocean water acidity in the context of climate change. The diagram begins by indicating the primary sources of carbon dioxide in the atmosphere, including industrial processes, fuel combustion. The diagram illustrates how carbon dioxide is partially absorbed by the ocean. Remains and carbon dioxide sink into the depths of the ocean. Additionally, the model allows for the measurement of water pH depending on the amount of dissolved carbon dioxide.