Difference between revisions of "Mixed strategy"
| Line 36: | Line 36: | ||
The battle of sexes is a two-players coordination game() in the game theory (). In this game there is one man and one woman, the woman prefers going to a ballet and the man prefers going to a baseball game. The nuance here is that they both prefers to go together rather than going alone to his/her prefered activity. The game combined with the respective utility is described in the table below. | The battle of sexes is a two-players coordination game() in the game theory (). In this game there is one man and one woman, the woman prefers going to a ballet and the man prefers going to a baseball game. The nuance here is that they both prefers to go together rather than going alone to his/her prefered activity. The game combined with the respective utility is described in the table below. | ||
| − | [[File:Battle1. | + | [[File:Battle1.jpg]] |
We can highlight the two pure Nash equilibrium: (Ballet, Ballet) and (Baseball, Baseball). To find the mixed strategy we need to asset some probabilities to each situation. Let '''<math>p</math>''' be the probability for the '''woman''' to go to the '''baseball''' game and '''<math>q</math>''' the probability for the '''men''' to go to the '''baseball''' game. The computations with the expected payoffs for each situation is display below. | We can highlight the two pure Nash equilibrium: (Ballet, Ballet) and (Baseball, Baseball). To find the mixed strategy we need to asset some probabilities to each situation. Let '''<math>p</math>''' be the probability for the '''woman''' to go to the '''baseball''' game and '''<math>q</math>''' the probability for the '''men''' to go to the '''baseball''' game. The computations with the expected payoffs for each situation is display below. | ||
| − | [[File:Battle2. | + | [[File:Battle2.jpg]] |
The payoff calculations are the same than// for the matching pennies(). For example, if the man goes to the baseball game he gets 3 when the woman goes also to the baseball game, with a <math>p</math> probability and 1 with a <math>1-p</math> probability (when she goes to the ballet). The expected payoff is then just the product of the probability and the payoff, for example for the last example the expected payoff is then <math>3p + 1(1-p) </math> | The payoff calculations are the same than// for the matching pennies(). For example, if the man goes to the baseball game he gets 3 when the woman goes also to the baseball game, with a <math>p</math> probability and 1 with a <math>1-p</math> probability (when she goes to the ballet). The expected payoff is then just the product of the probability and the payoff, for example for the last example the expected payoff is then <math>3p + 1(1-p) </math> | ||
| Line 46: | Line 46: | ||
A key aspect in the mixed strategy is the '''indifference''' of choosing one or another choice for a player. In the Battle of sexes game the Man has to be indifferent between going to the Baseball game and to the Ballet. This indifference or randomization between the choices of a player is expressed mathematically in our example for the man by <math>1+2p = 2-2p</math> which yields <math>p = 1/4 </math>. Then if the Woman is going to the Baseball game 1/4 of the time, the Man will be willing to randomize which event he attends. Similar calculation are made// for all possibilities and we multiply the probabilities to have the same denominator and we obtain the following table | A key aspect in the mixed strategy is the '''indifference''' of choosing one or another choice for a player. In the Battle of sexes game the Man has to be indifferent between going to the Baseball game and to the Ballet. This indifference or randomization between the choices of a player is expressed mathematically in our example for the man by <math>1+2p = 2-2p</math> which yields <math>p = 1/4 </math>. Then if the Woman is going to the Baseball game 1/4 of the time, the Man will be willing to randomize which event he attends. Similar calculation are made// for all possibilities and we multiply the probabilities to have the same denominator and we obtain the following table | ||
| − | [[File:Ballet3. | + | [[File:Ballet3.jpg]] |
We can note that 9 times over 16 the mixed strategy is (Baseball, Ballet) and it means that they are not together. Even if this mixed strategy Nash equilibrium seems to be undesirable, it's a Nash equilibrium as there is no improvement possible based on the behavior of the other party. This lack of coordination is often a feature of mixed strategy equilibrium. | We can note that 9 times over 16 the mixed strategy is (Baseball, Ballet) and it means that they are not together. Even if this mixed strategy Nash equilibrium seems to be undesirable, it's a Nash equilibrium as there is no improvement possible based on the behavior of the other party. This lack of coordination is often a feature of mixed strategy equilibrium. | ||
Revision as of 14:19, 5 January 2021
W.I.P Page in creation !!!
In his famous paper, John Forbes Nash proved that there is an equilibrium for every finite game. One can divide Nash equilibria into two types. Pure strategy Nash equilibria are Nash equilibria where all players are playing pure strategies. Mixed strategy Nash equilibria are equilibria where at least one player is playing a mixed strategy A game can have a pure-strategy or a mixed-strategy Nash equilibrium.
A pure strategy is an unconditional, defined choice that a person makes in a situation or game. A mixed strategy is an assignment of probability to all choices in the strategy set.
Definition
Mixed strategy: if the player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} has Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K} strategies Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle si1, si2, ...siK} available, a mixed strategy is a distribution of probabilities Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle pi=(pi1, pi2, ...piK)} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle pi1} is the probability for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} to choose the strategy Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle si1} As the mixed strategy is a distribution of probability there is: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sum_{j=1}^K pij = 1}
Nash equilibrium in mixed strategy
A mixed strategy Nash equilibrium involves at least one player playing a randomized strategy and no player being able to increase his or her expected payoff by playing an alternate strategy. A Nash equilibrium in which no player randomizes is called a pure strategy Nash equilibrium.
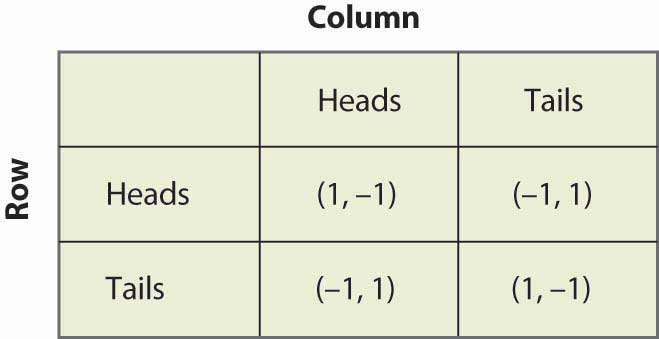
Example: Matching pennies
Suppose that Row believes Column plays Heads with probability Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p}
. If Row plays Heads, he gets 1 with probability Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p}
and –1 with probability Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (1-p)}
. His expected profit will be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1p - 1(1-p) = 2p - 1 }
. This is summarized in Figure below "Mixed strategy in matching pennies".
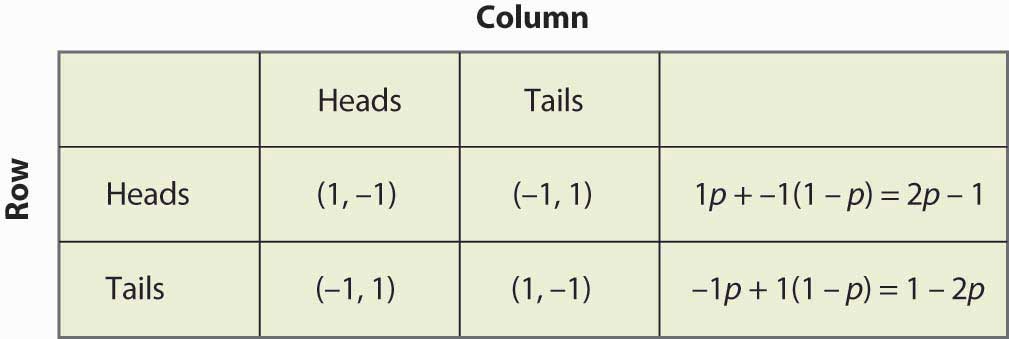
If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2p - 1 > 1 - 2p} , then Row is better off, on average, playing Heads than Tails. Similarly. If, on the other hand, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2p - 1 = 1 - 2p} so Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p=1/2} , then Row gets the same payoff no matter what Row does. In this case, Row could play Heads, could play Tails, or could flip a coin and randomize Row’s play.
Note that randomization requires equality of expected payoffs. If a player is supposed to randomize over strategy A or strategy B, then both of these strategies must produce the same expected payoff. Otherwise, the player would prefer one of them and wouldn’t play the other.
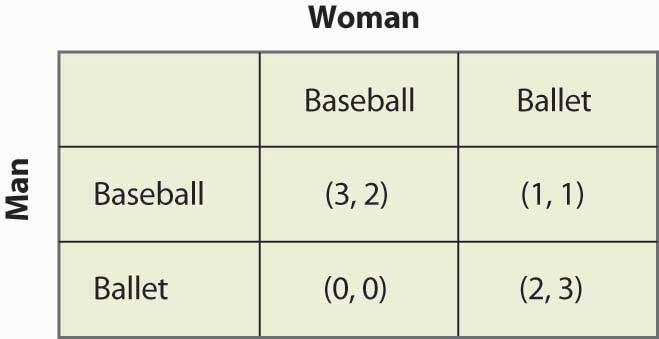
Mixed strategy in battle of the sexes
The battle of sexes is a two-players coordination game() in the game theory (). In this game there is one man and one woman, the woman prefers going to a ballet and the man prefers going to a baseball game. The nuance here is that they both prefers to go together rather than going alone to his/her prefered activity. The game combined with the respective utility is described in the table below.
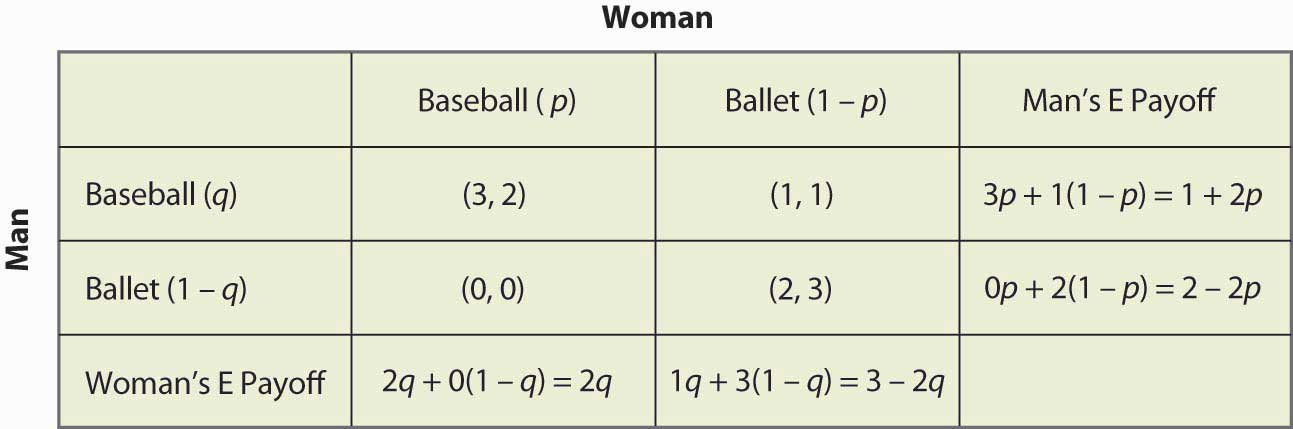
We can highlight the two pure Nash equilibrium: (Ballet, Ballet) and (Baseball, Baseball). To find the mixed strategy we need to asset some probabilities to each situation. Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p} be the probability for the woman to go to the baseball game and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q} the probability for the men to go to the baseball game. The computations with the expected payoffs for each situation is display below.
The payoff calculations are the same than// for the matching pennies(). For example, if the man goes to the baseball game he gets 3 when the woman goes also to the baseball game, with a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p} probability and 1 with a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1-p} probability (when she goes to the ballet). The expected payoff is then just the product of the probability and the payoff, for example for the last example the expected payoff is then Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 3p + 1(1-p) }
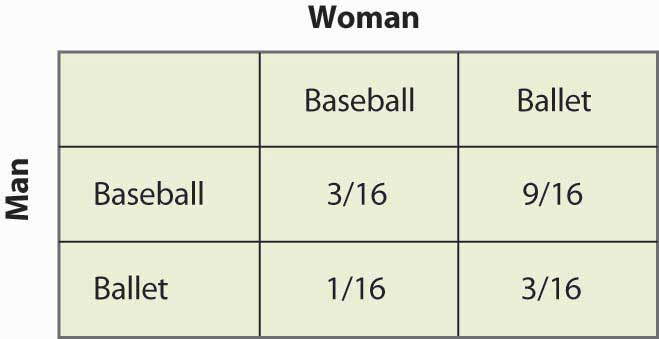
A key aspect in the mixed strategy is the indifference of choosing one or another choice for a player. In the Battle of sexes game the Man has to be indifferent between going to the Baseball game and to the Ballet. This indifference or randomization between the choices of a player is expressed mathematically in our example for the man by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1+2p = 2-2p} which yields Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p = 1/4 } . Then if the Woman is going to the Baseball game 1/4 of the time, the Man will be willing to randomize which event he attends. Similar calculation are made// for all possibilities and we multiply the probabilities to have the same denominator and we obtain the following table
We can note that 9 times over 16 the mixed strategy is (Baseball, Ballet) and it means that they are not together. Even if this mixed strategy Nash equilibrium seems to be undesirable, it's a Nash equilibrium as there is no improvement possible based on the behavior of the other party. This lack of coordination is often a feature of mixed strategy equilibrium.