Difference between revisions of "Mixed strategy"
| Line 21: | Line 21: | ||
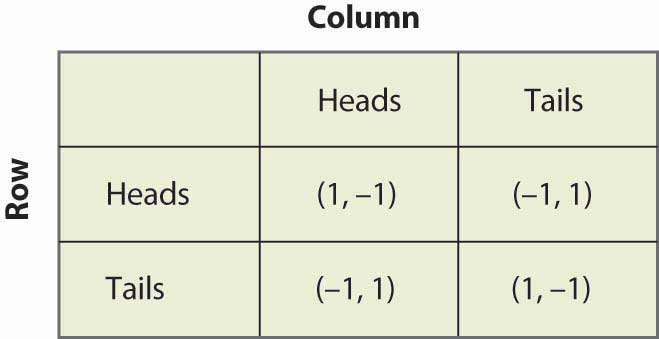
Example: Matching pennies | Example: Matching pennies | ||
| − | [[File:[ | + | [[File:Penny1.jpeg]] |
| + | |||
| + | Suppose that Row believes Column plays Heads with probability <math>p</math>. If Row plays Heads, he gets 1 with probability <math>p</math> and –1 with probability <math> (1–p) </math>. His expected profit will be <math> 1p - 1(1-p) = 2p – 1 </math>. This is summarized in Figure below "Mixed strategy in matching pennies". | ||
| + | [[File:Penny2.jpeg]] | ||
| + | |||
| + | If <math>2p – 1 > 1 – 2p</math>, then Row is better off, on average, playing Heads than Tails. Similarly. If, on the other hand, <math>2p – 1 = 1 – 2p</math>, then Row gets the same payoff no matter what Row does. In this case, Row could play Heads, could play Tails, or could flip a coin and randomize Row’s play. | ||
Revision as of 12:23, 29 December 2020
W.I.P Page in creation !!!
In his famous paper, John Forbes Nash proved that there is an equilibrium for every finite game. One can divide Nash equilibria into two types. Pure strategy Nash equilibria are Nash equilibria where all players are playing pure strategies. Mixed strategy Nash equilibria are equilibria where at least one player is playing a mixed strategy A game can have a pure-strategy or a mixed-strategy Nash equilibrium.
A pure strategy is an unconditional, defined choice that a person makes in a situation or game. A mixed strategy is an assignment of probability to all choices in the strategy set.
Definition
Mixed strategy: if the player Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} has Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle K} strategies Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle si1, si2, ...siK} available, a mixed strategy is a distribution of probabilities Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle pi=(pi1, pi2, ...piK)} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle pi1} is the probability for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle i} to choose the strategy Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle si1} As the mixed strategy is a distribution of probability there is: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sum_{j=1}^K pij = 1}
Nash equilibrium in mixed strategy
A mixed strategy Nash equilibrium involves at least one player playing a randomized strategy and no player being able to increase his or her expected payoff by playing an alternate strategy. A Nash equilibrium in which no player randomizes is called a pure strategy Nash equilibrium.
Example: Matching pennies
Suppose that Row believes Column plays Heads with probability Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p}
. If Row plays Heads, he gets 1 with probability Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p}
and –1 with probability Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (1–p) }
. His expected profit will be Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 1p - 1(1-p) = 2p – 1 }
. This is summarized in Figure below "Mixed strategy in matching pennies".
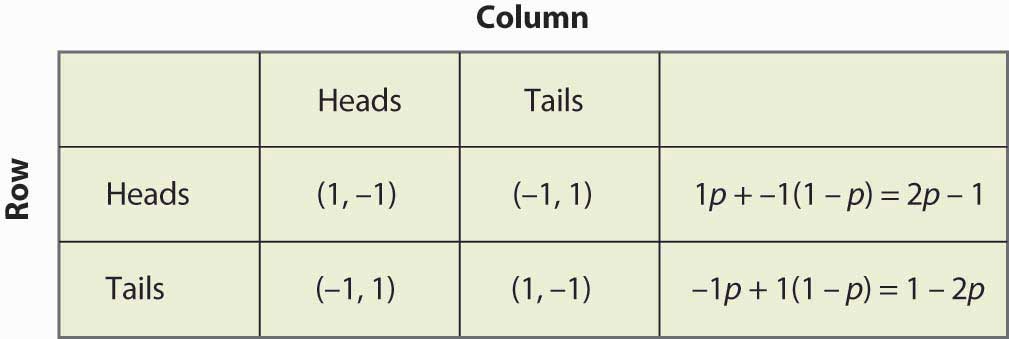
If Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2p – 1 > 1 – 2p} , then Row is better off, on average, playing Heads than Tails. Similarly. If, on the other hand, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle 2p – 1 = 1 – 2p} , then Row gets the same payoff no matter what Row does. In this case, Row could play Heads, could play Tails, or could flip a coin and randomize Row’s play.