Difference between revisions of "Ideal latency between a metro trains"
(→Passengers at stations) |
m |
||
| (7 intermediate revisions by the same user not shown) | |||
| Line 14: | Line 14: | ||
=What is the target of this model?= | =What is the target of this model?= | ||
Try to get: | Try to get: | ||
| − | 1) The biggest value at the transport capacity graph | + | 1) The biggest value at the transport capacity graph |
| − | 2) Minimized number of waiting passagers in stations at “passagers at stations” graph | + | 2) Minimized number of waiting passagers in stations at “passagers at stations” graph |
| − | 3) Avoid the traffic jam | + | 3) Avoid the traffic jam |
| − | 4) Less people at station (you will see the red flash when is overcrowded) | + | 4) Less people at station (you will see the red flash when is overcrowded) |
=Global variables= | =Global variables= | ||
| Line 56: | Line 56: | ||
If this happens the following trains are waiting in the tunnel for departure from station of previous train. | If this happens the following trains are waiting in the tunnel for departure from station of previous train. | ||
User can choose attribute value station_ranks (slider rank_xx) for each station. High number represent high probability that passenger exit the train in that station. | User can choose attribute value station_ranks (slider rank_xx) for each station. High number represent high probability that passenger exit the train in that station. | ||
| + | |||
| + | |||
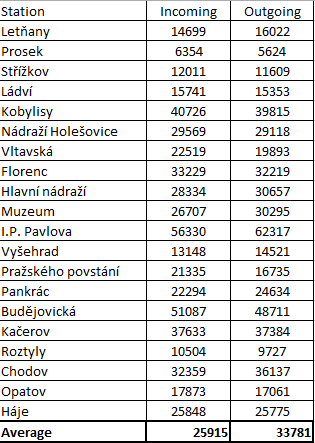
| + | Incoming and outgoing passengers at stations | ||
| + | |||
| + | [[File:Pass_num.png]] | ||
| + | |||
| + | Sources: http://geography.upol.cz/soubory/studium/bp/2014-rg/2014_Nezval.pdf | ||
=Model= | =Model= | ||
| − | I developed a one-way traffic simulation based on real data obtained from the annual report and DPP study | + | I developed a one-way traffic simulation based on real data obtained from the |
| + | [http://www.dpp.cz/download-file/8795/annual_report_2013.pdf annual report] and [http://geography.upol.cz/soubory/studium/bp/2014-rg/2014_Nezval.pdf DPP study]. | ||
Each station has set ratio on a scale from zero to one, which indicates the probability of outgoing passengers in the station. | Each station has set ratio on a scale from zero to one, which indicates the probability of outgoing passengers in the station. | ||
The lowest value has station Prosek (0.07), while the I.P. Pavlova has the highest value of (0.79) – as you can see in the chart. | The lowest value has station Prosek (0.07), while the I.P. Pavlova has the highest value of (0.79) – as you can see in the chart. | ||
Because it is a one-way simulation the first station (Letňany) has incoming passengers, so the station does not show any ratio. | Because it is a one-way simulation the first station (Letňany) has incoming passengers, so the station does not show any ratio. | ||
Station Haje has only outgoing passengers because there is not any next station to go. | Station Haje has only outgoing passengers because there is not any next station to go. | ||
| − | There are two time zones in the simulation - the first one is peak, which takes place in time from 7am to 9am and from | + | There are two time zones in the simulation - the first one is peak, which takes place in time from 7am to 9am and from 4pm to 6pm and second one dedicated to off-peak time. |
Default delay between trains is set to 76 ticks. | Default delay between trains is set to 76 ticks. | ||
| Line 77: | Line 85: | ||
An analysis based on simulation, I found that if the train delay between trains is set to less than 76 or more than 81 seconds, trains start to wait in tunnel between stations to departure of the previous train. The value that avoids overcrowding station and trains are effectively filled, moves around xy seconds. | An analysis based on simulation, I found that if the train delay between trains is set to less than 76 or more than 81 seconds, trains start to wait in tunnel between stations to departure of the previous train. The value that avoids overcrowding station and trains are effectively filled, moves around xy seconds. | ||
Transport capacity is about 26,900 persons per hour at peak. Simulation has only half value because of one-way traffic. | Transport capacity is about 26,900 persons per hour at peak. Simulation has only half value because of one-way traffic. | ||
| + | |||
| + | Ideal setting (76 seconds delay between the trains) | ||
| + | [[File:peak_ideal.png]] | ||
| + | [[File:ideal3.jpg]] | ||
| + | |||
| + | Traffic jam (train waiting in tunnel) when I set up 66 seconds delay between the trains. | ||
| + | [[File:peak.png]] | ||
| + | |||
| + | Traffic jam (train waiting in tunnel) when I set up 86 seconds delay between the trains. | ||
| + | [[File:peak2.png]] | ||
===Off-peak=== | ===Off-peak=== | ||
Value is reduced occurrence of new passengers (add_pass_delay) on 63 seconds during the off-peak. This was set because of fact, that there are only 12,600 passengers per hour at this time, which is 2,1 times less than at the peak. | Value is reduced occurrence of new passengers (add_pass_delay) on 63 seconds during the off-peak. This was set because of fact, that there are only 12,600 passengers per hour at this time, which is 2,1 times less than at the peak. | ||
| − | Trains are effectively fulffiled when the values are set up to 311 second. Trains are overcrowded if the value is higher than that. | + | Trains are effectively fulffiled when the values are set up to 311 second. Trains are overcrowded if the value is higher than that. Minimum delay between the trains it could be set up to 36 seconds if you choose less than that the trains will be jammed. |
| + | |||
| + | Minimum delay between the trains (value is set up to 36) | ||
| + | [[File:of36.png]] | ||
| + | |||
| + | [[File:of36_2.png]] | ||
| + | [[File:of36_3.png]] | ||
=Conslusion= | =Conslusion= | ||
| Line 90: | Line 114: | ||
Model could be extended in the future - there are some possibilities like as adding depot for some trains (you know - like Kačerov where some trains terminates) or the line from station Háje to station Letňany. | Model could be extended in the future - there are some possibilities like as adding depot for some trains (you know - like Kačerov where some trains terminates) or the line from station Háje to station Letňany. | ||
And of course due to option to change number of station and a lot of variables you could build your own metro. | And of course due to option to change number of station and a lot of variables you could build your own metro. | ||
| + | |||
| + | =Code= | ||
| + | [[File:Metro.nlogo]] | ||
Latest revision as of 18:29, 29 January 2015
Simulation should represent what latency can be set for passagers transport in the Prague metro (depending on the density of passagers).
Contents
Assignment
Project Name: Ideal latency between a metro trains Author: Bc. Jan Cestr Software used: NetLogo Class: 4IT496 Simulation of Systems (WS 2014/2015)
Object
Finding the minimum and maximum limits (time) for the Prague metro (Line C) which would reveal ideal spacing of each metro trains. Train should not stop in the tunnel due to waiting for the previous train (apart from exceptional cases). It should be reckon with the fact that metro station can’t be overfull.
What is the target of this model?
Try to get:
1) The biggest value at the transport capacity graph 2) Minimized number of waiting passagers in stations at “passagers at stations” graph 3) Avoid the traffic jam 4) Less people at station (you will see the red flash when is overcrowded)
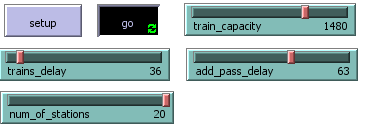
Global variables
train_capacity
Capacity of one train. One graphic character depicts ten real people.
trains_Delay
Indicates the spacing between trains
add_pass_delay
Speed rate of arrival passagers
num of stations
Set the number of stations in model. Model is adapting scale by this value
rank_xy
Set the rank of outcoming passagers
Graphs:
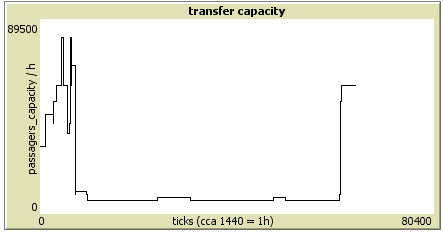
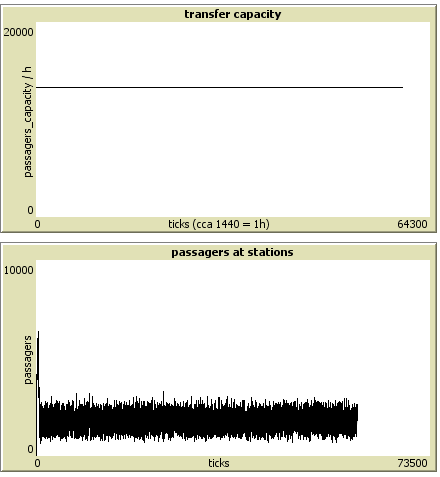
transfer capacity
The graph show the capacity of subway per hour . There is describe that about 1440 tickes is one real hour and graph show capacity of passagers per hour. Wikipedia show that subway metro (C) transport about 26,900 per hour in high-peak – it’s nearly the same amount as in the model.
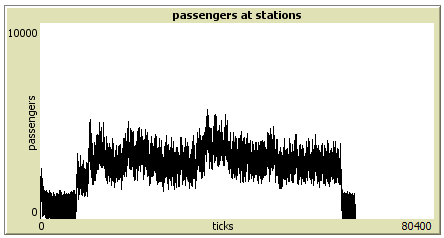
Passengers at stations
Number of passagers whose waiting on train. Passagers whose leaves the train are not count in this graph.
How does the simulation work
Each station has set a parameter stations_min stations_max which indicating the number of people who may come to the station together (it's the random number from the specified minimum to maximum). So it‘s clear that the final station must be set to 0. People turn red if the station is overcrowded – in this situation another people cannot come to this station. Each passenger has set station_id that indicate the station ID which is going to get off. Outgoing passagers are shown under the platform in the model, after a while they disappear (offcourse - station_id is not set after that). In the station can not be two trains at one time. The train could delay in station due to large number of incoming and outgoing passager (it‘s added 0.5 tick to waiting for train departures for each one). If this happens the following trains are waiting in the tunnel for departure from station of previous train. User can choose attribute value station_ranks (slider rank_xx) for each station. High number represent high probability that passenger exit the train in that station.
Incoming and outgoing passengers at stations
Sources: http://geography.upol.cz/soubory/studium/bp/2014-rg/2014_Nezval.pdf
Model
I developed a one-way traffic simulation based on real data obtained from the annual report and DPP study. Each station has set ratio on a scale from zero to one, which indicates the probability of outgoing passengers in the station. The lowest value has station Prosek (0.07), while the I.P. Pavlova has the highest value of (0.79) – as you can see in the chart. Because it is a one-way simulation the first station (Letňany) has incoming passengers, so the station does not show any ratio. Station Haje has only outgoing passengers because there is not any next station to go. There are two time zones in the simulation - the first one is peak, which takes place in time from 7am to 9am and from 4pm to 6pm and second one dedicated to off-peak time.
Default delay between trains is set to 76 ticks. I recommended you to try and set the biggest rank for the “big“ stations with set minimum and maximum. But as you can see – it still works.
How to set up typical day?
When simulation started it could be the best setup long period in the parameter add_pass_delay. I think that you know why - it‘s morning, it means less people there. After that I recommended to you goes to the high-peak gradually. If you don’t do this, some of the station will be overcrowded in high-peak meanwhile the first train goes to the end station.
Results
From the information obtained on the Internet, it was found that metro is almost always full at peak, which indicates the validity of this simulation model. There are about 19 metro trains per hour in the simulation, which also corresponds with a reality (in fact, there are 39 trains in peak but this value has half value because of one-way traffic simulation).
Peak
An analysis based on simulation, I found that if the train delay between trains is set to less than 76 or more than 81 seconds, trains start to wait in tunnel between stations to departure of the previous train. The value that avoids overcrowding station and trains are effectively filled, moves around xy seconds. Transport capacity is about 26,900 persons per hour at peak. Simulation has only half value because of one-way traffic.
Ideal setting (76 seconds delay between the trains)
Traffic jam (train waiting in tunnel) when I set up 66 seconds delay between the trains.

Traffic jam (train waiting in tunnel) when I set up 86 seconds delay between the trains.

Off-peak
Value is reduced occurrence of new passengers (add_pass_delay) on 63 seconds during the off-peak. This was set because of fact, that there are only 12,600 passengers per hour at this time, which is 2,1 times less than at the peak. Trains are effectively fulffiled when the values are set up to 311 second. Trains are overcrowded if the value is higher than that. Minimum delay between the trains it could be set up to 36 seconds if you choose less than that the trains will be jammed.
Minimum delay between the trains (value is set up to 36)

Conslusion
It seems that ratio which is set up today at peak is ideal. The trains If the company has set another time trains would be jammed. So 'high five' to DPP :) At off-peak I found ideal latency between metro at value which represents 5 minutes - so it's almost identical to typical working day.
In real life is delay sometimes set up to less time than we analyzed, so it seems that company is not effective, but you know - it’s probably for increased comfort for passengers who don’t want to wait.
Model could be extended in the future - there are some possibilities like as adding depot for some trains (you know - like Kačerov where some trains terminates) or the line from station Háje to station Letňany. And of course due to option to change number of station and a lot of variables you could build your own metro.