Difference between revisions of "Causal Loop Diagram/cs"

From Simulace.info
Jump to: navigation, search
(→‎Negativní (vyrovnávací) zpětnovazební smyčka)
(→‎Příklady k procvičení)
 
(40 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
=Úvod=
 
=Úvod=
 
[[File:cld_sheepd.png|thumb|diagram kauzálních smyček]]
 
[[File:cld_sheepd.png|thumb|diagram kauzálních smyček]]
−
==Příběh na začátek==
+
Diagramy kauzálních smyček (v angličtině Casual Loop Diagrams) slouží k zachycení vzathů mezi proměnnými (elementy) [[System Dynamics/cs|dynamických systémů]] a patří mezi základní nástroje při jejich analýze. Umožňuje vidět základní strukturu a vlastnosti dynamického systému bez toho bez zatížení detaily, které musíme řešit, když chceme chování systému simulovat. Modelování systému obvykle začíná vytvořením CLD diagramu, který slouží jako základ pro budoucí tvorbu simulace. Často slouží jako podklady pro tvorbu [[Stock and Flow Diagram/cs|stock and flow diagramů]].
 +
 
 +
Diagramy jsou tvořeny dvěmi základními typy smyček: pozitivní zpětnovazební smyčkou a negativní zpětnovazební smyčkou. Z kombinací těchchto dvou typů smyček lze modelovat libovolně složité dynamické systémy.<ref> Hayward J., Introduction To System Dynamics [online].
 +
[cit. 2013-06-15]. Dostupné z: http://www.churchmodel.org.uk/introsystems.pdf </ref>
 +
 
 +
Nejdříve se podíváme na notaci CLD diagramů, poté si ukážeme základní typy smyček v diagramu a chování systému, které jim odpovídá a nakonec si uvedeme praktický návod, jak přistupovat k tvorbě diagramů kauzálních smyček.
  
 
=Syntaxe diagramů kauzálních smyček=
 
=Syntaxe diagramů kauzálních smyček=
−
Diagramy kauzálních smyček používají jednoduchou notaci. Názvy elementů v systému jsou vepsány do diagramu a vztah mezi nimi je dán šipkami, které je spojují. Pomocí matematických znamének je potom vyjádřen směr závislosti.
+
Diagramy kauzálních smyček používají jednoduchou notaci. Názvy elementů v systému jsou vepsány do diagramu a vztah mezi nimi je dán šipkami, které je spojují. Pomocí matematických znamének je potom vyjádřen směr závislosti.  
  
 
== Element (proměnná) systému ==  
 
== Element (proměnná) systému ==  
Line 11: Line 16:
 
== Vztahy mezi elementy ==
 
== Vztahy mezi elementy ==
 
Vztahy mezi elementy systému jsou znázorněny šipkami. Vztah mezi dvěmi elementy může být buď pozitivní (''pokud se zvýší A, zvýší se i B''), nebo negativní (''pokud se zvýší A, sníží se B'').
 
Vztahy mezi elementy systému jsou znázorněny šipkami. Vztah mezi dvěmi elementy může být buď pozitivní (''pokud se zvýší A, zvýší se i B''), nebo negativní (''pokud se zvýší A, sníží se B'').
−
Pozitivní vazba se značí pomocí znaménka "+" na konci šipky, zatímco negativní vztah se značí pomocí "-".  
+
Pozitivní vazba se značí pomocí znaménka "+" na konci šipky, zatímco negativní vztah se značí pomocí "-".<ref> North K., An Introduction to Systems Thinking - How to Read Causal Loop Diagrams (CLDs) [online].
 +
[cit. 2013-06-17]. Dostupné z: http://courses.umass.edu/plnt597s/KarlsArticle.pdf </ref>
  
 
'''Pozitivní vztah mezi elementy systému:'''
 
'''Pozitivní vztah mezi elementy systému:'''
Line 54: Line 60:
 
[[File:cld_negative_feedback_vensim_symbol.png]] (nástroj Vensim)
 
[[File:cld_negative_feedback_vensim_symbol.png]] (nástroj Vensim)
  
−
==Příklady==
 
  
 
=Typy smyček v diargamech=
 
=Typy smyček v diargamech=
−
Pomocí smyček v diagramech lze zachytit typická chování dynamického systému. I když se systém obvykle chová mnohem komplexněji, než níže uvedené příklady, tak jejich chování vzniká právě z těchto primitivních interakcí.
+
Pomocí smyček v diagramech lze zachytit typická chování dynamického systému. I když se systém obvykle chová mnohem komplexněji, než níže uvedené příklady, tak jejich chování vzniká právě z těchto primitivních interakcí.<ref> Kirkwood, System Behavior and
 +
Causal LoopDiagrams, 1.4 System Structure and Patterns of Behavior
 +
[online].
 +
[cit. 2013-06-15]. Dostupné z: http://www.public.asu.edu/~kirkwood/sysdyn/SDIntro/ch-1.pdf </ref>
  
 
== Pozitivní zpětnovazební smyčka ==
 
== Pozitivní zpětnovazební smyčka ==
Line 87: Line 95:
  
 
Element ''požadovaná telpota'', je externím prvkem, který pro zpětnovazební smyčku určuje cílové hodnoty jednotlivých proměnných.
 
Element ''požadovaná telpota'', je externím prvkem, který pro zpětnovazební smyčku určuje cílové hodnoty jednotlivých proměnných.
 +
 +
 +
{{ambox
 +
| type      = notice
 +
| text      = '''Jak jednoduše určit, zda je daná smyčka pozitivní nebo negativní?'''
 +
 +
Stačí spočítat, kolik je negativních vazeb v dané smyčce<ref> Kirkwood, System Behavior and
 +
Causal LoopDiagrams, 1.3 Feedback and Causal Loop Diagrams [online].
 +
[cit. 2013-06-15]. Dostupné z: http://www.public.asu.edu/~kirkwood/sysdyn/SDIntro/ch-1.pdf </ref>:
 +
* '''Smyčka je pozitivní''' zpětnou vazbou, pokud má '''sudý (nebo nulový) počet negativních vazeb''' mezi elementy.
 +
* '''Smyčka je negativní (vyrovnávací)''' zpětnou vazbou, pokud má '''lichý počet negativních vazeb''' mezi elementy.
 +
 +
}}
  
 
== Negativní zpětnovazební smyčka se spožděním ==
 
== Negativní zpětnovazební smyčka se spožděním ==
 +
Negativní zpětnovazební smyčka s dostatečně velkým zpožděním může vést k oscilaci hodnot elementů, které jsou do ní zapojené. V některých případech systém osciluje do nekonečna, v jiných případech se oscilace zmenšuje díky tomu jak zpětnovazební smyčka postupně přibližuje hodnoty elementů k cílové hodnotě.
 +
 +
[[File:cld_behaviour_oscilating.png]]
 +
 +
Typickým příkladem systému s oscilujícími zpětnovazebními smyčkami jsou výrobní systémy. Jsou způsobeni zpožděním, které je mezi aktuální poptávkou zákazníka po produktu a času, který je potřebný pro jeho vyrobení a dodání. Často se tak stává, že se prodává ze zásob, které se tím zmenšují, protože produkce nestačí dodávat výrobky včas a nebo se naopak hromadí zásoby, protože poptávka klientů se očekávala vyšší, než nakonec byla.
 +
 +
[[File:cld_oscilating_loop.png|540px]]
  
 
== Kombinace pozitivní a negativní zpětnovazební smyčky ==
 
== Kombinace pozitivní a negativní zpětnovazební smyčky ==
−
==Příklady==
+
 
 +
Model systému může začít vykazovat rozličné vzorce chování ve chvíli, kdy v diagramu začneme kombinovat pozitivní a negativní zpětnovazební smyčky. Jedním z nejobvyklejších je limitovaný exponenciální růst klíčového elemtnu (průběh jeho hodnoty je ve tvaru S-Křivky). V takovém systému proměnná nejdříve exponenciálně roste díky vlivu pozitivní zpětnovazební smyčky. Její růst je ale limitován negativní zpětnovazební smyčkou, která určuje maximální možnou hodnotu, na kterou se může hodnota elementu dostat.
 +
 
 +
[[File:cld_behaviour_sshape.png]]
 +
 
 +
Toto chování si ukážeme na příkladu populace ovcí, který žije na pastvině s omezeným zdrojem potravy. Množství trávy na pastvině je dané její velikostí. Ze začátku populace ovcí roste exponenciálně, protože její velikost je daleko od limitu, který je dán množstvím trávy na pastvině. Ve chvíli, kdy rostoucí populace ovcí začne spásat trávu rychleji, než stačí dorůstat nová, tak se růst populace postupně spomalí dokud se neustálí na maximální možné výši.
 +
 
 +
 
 +
[[File:cld_diagram_sheep.png]]
 +
 
 +
Skoro každý exponenciální růst v dynamickém systému nakonec narazí na nějaký limit daný negativní zpětnovazební smyčkou. Růst organizace, růst prodejů nebo růst populací jsou typickými příklady tohoto chování.
  
 
= Postup tvorby diagramu kauzálních smyček =
 
= Postup tvorby diagramu kauzálních smyček =
Line 114: Line 152:
 
# Pokud šipka mezi dvěma elementy vyžaduje mnoho vysvětlování, pravděpodobně by bylo vhodné přidat mezi již existující proměnné další element, který osvětlí, co se v systému děje.
 
# Pokud šipka mezi dvěma elementy vyžaduje mnoho vysvětlování, pravděpodobně by bylo vhodné přidat mezi již existující proměnné další element, který osvětlí, co se v systému děje.
 
# Snažte se diagram držet co nejjednodušší (při dodržení výše uvedených bodů). Účel diagramu není popsat každý detail zvoleného procesu v systému ale spíše ukázat podstatné aspekty struktury zpětné vazby, které způsobují pozorované chování elementů (proměnných) v systému.
 
# Snažte se diagram držet co nejjednodušší (při dodržení výše uvedených bodů). Účel diagramu není popsat každý detail zvoleného procesu v systému ale spíše ukázat podstatné aspekty struktury zpětné vazby, které způsobují pozorované chování elementů (proměnných) v systému.
 +
 +
=VenSim - Nástroj pro vytváření diagramů kauzálních smyček=
 +
[[File:cld_vensim_screenshot.png|thumb|Uživatelské rozhraní nástroje VenSim]]
 +
Jedním z nástrojů, který lze použít k modelování diagramů kauzálních smyček je nástroj VenSim, který je zdarma dostupný pro nekomerční použití. VenSim lze [http://vensim.com/free-download/ stáhnout z oficiální stránky jeho výrobce]. Kromě vytváření diagramů kauzálních smyček umožňuje tento nástroj tvorbu [[ Stock and Flow Diagram/cs|Stock And Flow Diagramů]]. Umožňuje simulaci vytvořených modelů, generování stomů příčin a následků a identifikaci zpětnovazebních smyček.<ref> VenSim, Vensim Software [online].
 +
[cit. 2013-06-17]. Dostupné z: http://vensim.com/vensim-software/ </ref>:
 +
 +
=Příklady k procvičení=
 +
 +
 +
U následujících diagramů určete, zda chování jejich hodnot bude vykazovat exponenciální růst, hledání hodnoty, oscilace nebo S-Křivku:
 +
 +
'''a) Protinflační opatření ČNB:'''
 +
 +
[[File:cld_ex1_osc.png|Intervence ČNB|640px]]
 +
 +
 +
 +
'''b) Gravitace'''
 +
 +
[[File:cld_ex1_pos_feed2.png|Gravitace|]]
 +
 +
 +
 +
'''c) Bankovní účet'''
 +
 +
[[File:cld_ex1_pos_feed.png|Gravitace|]]
 +
 +
 +
'''d) Generický diagram''' (Určete chování proměnné ''A'')
 +
 +
[[File:cld_ex1_neg.png|Generický diagram|]]
 +
 +
 +
'''e) Vývoj prodejů''' (určete chování proměnné ''Prodeje'')
 +
 +
[[File:cld_ex1_sshape.png|Vývoj prodejů|]]
 +
 +
 +
'''f) Studentský syndrom'''
 +
 +
[[File:cld_ex1_neg2.png|Studentský syndrom|]]
  
  
−
==Příklady==
+
''Řešení: a)Oscilace b)Exponenciální růst c)Exponenciální růst d)Exponenciální růst e)S-Křivka f) Hledání hodnoty  ''
  
 
=Reference=
 
=Reference=
  
 
<references/>
 
<references/>

Latest revision as of 13:00, 17 June 2014

Úvod

diagram kauzálních smyček

Diagramy kauzálních smyček (v angličtině Casual Loop Diagrams) slouží k zachycení vzathů mezi proměnnými (elementy) dynamických systémů a patří mezi základní nástroje při jejich analýze. Umožňuje vidět základní strukturu a vlastnosti dynamického systému bez toho bez zatížení detaily, které musíme řešit, když chceme chování systému simulovat. Modelování systému obvykle začíná vytvořením CLD diagramu, který slouží jako základ pro budoucí tvorbu simulace. Často slouží jako podklady pro tvorbu stock and flow diagramů.

Diagramy jsou tvořeny dvěmi základními typy smyček: pozitivní zpětnovazební smyčkou a negativní zpětnovazební smyčkou. Z kombinací těchchto dvou typů smyček lze modelovat libovolně složité dynamické systémy.[1]

Nejdříve se podíváme na notaci CLD diagramů, poté si ukážeme základní typy smyček v diagramu a chování systému, které jim odpovídá a nakonec si uvedeme praktický návod, jak přistupovat k tvorbě diagramů kauzálních smyček.

Syntaxe diagramů kauzálních smyček

Diagramy kauzálních smyček používají jednoduchou notaci. Názvy elementů v systému jsou vepsány do diagramu a vztah mezi nimi je dán šipkami, které je spojují. Pomocí matematických znamének je potom vyjádřen směr závislosti.

Element (proměnná) systému

Elementy v systému jsou v diagramu reprezentovány jejich názvem. Pro název elementu se obvykle používá podstatné jméno ("populace", "prodeje", "znečištění" atd...).

Vztahy mezi elementy

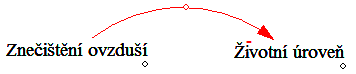
Vztahy mezi elementy systému jsou znázorněny šipkami. Vztah mezi dvěmi elementy může být buď pozitivní (pokud se zvýší A, zvýší se i B), nebo negativní (pokud se zvýší A, sníží se B). Pozitivní vazba se značí pomocí znaménka "+" na konci šipky, zatímco negativní vztah se značí pomocí "-".[2]

Pozitivní vztah mezi elementy systému:

Cld positive link.png


Negativní vztah mezi elementy systému:

Cld negative link.png


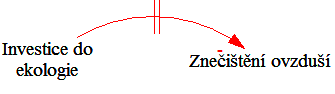
Je potřeba do diagramu vyznačit zpoždění, které je mezi příčinou a následkem pokud je významné pro dynamiku modelovaného systému. Zpoždění má symbol dvou svislých čar přes spojovací šipku:

Cld negative delay.png


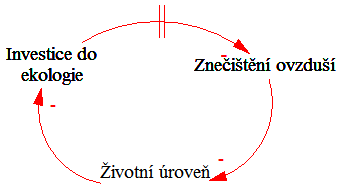
Spojením několika elementů do jednoho cyklu vzniká zpětnovazební smyčka:


Cld loop.png

Označení pozitivních a negativních zpětnovazebních cyklů

Pro jasný přehled o tom, je cyklus svojí povahou pozitivní nebo negativní se používají symboly, které se vepisují dovnitř kauzálních smyček[3].

Symboly pro pozitivní zpětnovazební smyčku:

Cld positive feedback symbol.png (Kirkwood)

Cld positive feedback vensim symbol.png (nástroj Vensim)


Symboly pro negativní zpětnovazební smyčku:

Cld negative feedback symbol.png (Kirkwood)

Cld negative feedback vensim symbol.png (nástroj Vensim)


Typy smyček v diargamech

Pomocí smyček v diagramech lze zachytit typická chování dynamického systému. I když se systém obvykle chová mnohem komplexněji, než níže uvedené příklady, tak jejich chování vzniká právě z těchto primitivních interakcí.[4]

Pozitivní zpětnovazební smyčka

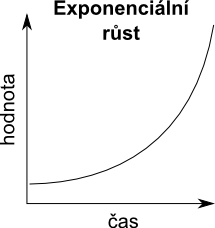
Pozitivní zpětnovazební smyčka vyjadřuje vztah mezi elementy, ve kterém zvýšení hodnoty jednoho z nich vyvolá zvýšení hodnoty dalších elementů a ty poté svojí zvýšenou hodnotou způsobí navýšení hodnoty původního elementu. Tento typ smyčky se vyznačuje exponenciálním růstem (tj. hodnoty elementů ve smyčce rostou neustále se zvyšující rychlostí).

Cld behaviour exponential.png

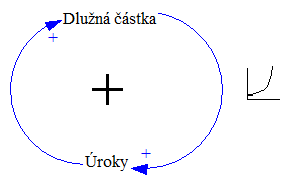
Z počátku se růst může zdát pomalý a to může pozorovatele mást, ale z podstaty exponenciálního chování vyplývá, že se bude rapidně zrychlovat. Pokud máte v systému problém, který je součástí pozitivní zpětnovazební smyčky a v tuto chvíli se zdá malý (problém neroste tak rychle), tak velmi brzo vám díky exponenciálnímu charakteru zpětnovazební smyčky může přerůst přes hlavu a na jeho řešení již bude pozdě. Příkladem může být situace, kdy někomu dlužíte a začínají vám nabíhat úroky:

Cld debt.png


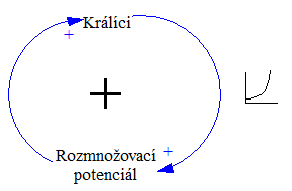
Trošku příjemnějším příkladem může být například chování kolonie králíků v případě, že mají prakticky neomezené množství potravy. Množství králíků se bude exponenciálně zvyšovat:

Cld rabbits.png

V cizojazyčné literatuře jsou pozitivní zpětnovazební smyčky často označovány za "vicious circles" nebo "virtuous circles" (dle toho, jestli směr změny je žádoucí). Exponenciální chování takového systému se pak často označuje termínem "bandwagon effect" nebo také "snowballing" (efekt sněhové koule).

Negativní (vyrovnávací) zpětnovazební smyčka

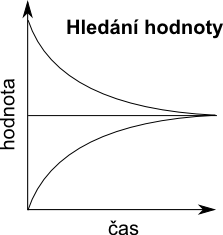
Negativní, neboli vyrovnávací zpětnovazební smyčka přivádí postupně elementy v ní obsažené k jejích cílové hodnotě, která je do smyčky dodána nějakým vnějším elementem.

Pokud je hodnota elemntu ve smyčce pod cílovou hodnotou, smyčka způsobí, že začne jeho hodnota růst, dokud nedosáhne požadované hodnoty. Naopak, pokud je hodnota elementu nad cílovou hodnotou, smyčka způsobí, že začne jeho hodnota klesat, aby se dostana na kýženou cílovou hodnotu.

Cld negative behaviour.png

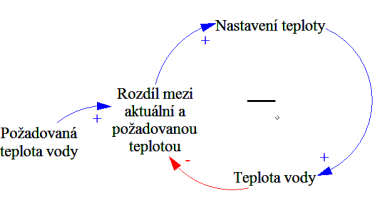
Jako příklad si uveďme diagram znázorňující regulaci vody sprchujícím se člověkem:

Cld negative loop.png

Element požadovaná telpota, je externím prvkem, který pro zpětnovazební smyčku určuje cílové hodnoty jednotlivých proměnných.


Jak jednoduše určit, zda je daná smyčka pozitivní nebo negativní?

Stačí spočítat, kolik je negativních vazeb v dané smyčce[5]:

  • Smyčka je pozitivní zpětnou vazbou, pokud má sudý (nebo nulový) počet negativních vazeb mezi elementy.
  • Smyčka je negativní (vyrovnávací) zpětnou vazbou, pokud má lichý počet negativních vazeb mezi elementy.

Negativní zpětnovazební smyčka se spožděním

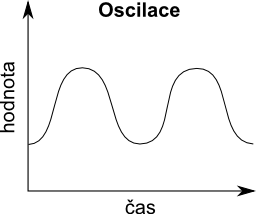
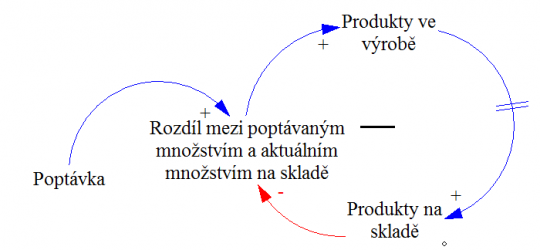
Negativní zpětnovazební smyčka s dostatečně velkým zpožděním může vést k oscilaci hodnot elementů, které jsou do ní zapojené. V některých případech systém osciluje do nekonečna, v jiných případech se oscilace zmenšuje díky tomu jak zpětnovazební smyčka postupně přibližuje hodnoty elementů k cílové hodnotě.

Cld behaviour oscilating.png

Typickým příkladem systému s oscilujícími zpětnovazebními smyčkami jsou výrobní systémy. Jsou způsobeni zpožděním, které je mezi aktuální poptávkou zákazníka po produktu a času, který je potřebný pro jeho vyrobení a dodání. Často se tak stává, že se prodává ze zásob, které se tím zmenšují, protože produkce nestačí dodávat výrobky včas a nebo se naopak hromadí zásoby, protože poptávka klientů se očekávala vyšší, než nakonec byla.

Cld oscilating loop.png

Kombinace pozitivní a negativní zpětnovazební smyčky

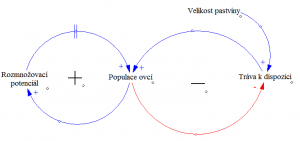
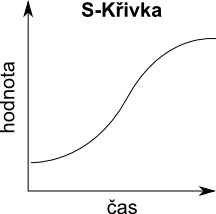
Model systému může začít vykazovat rozličné vzorce chování ve chvíli, kdy v diagramu začneme kombinovat pozitivní a negativní zpětnovazební smyčky. Jedním z nejobvyklejších je limitovaný exponenciální růst klíčového elemtnu (průběh jeho hodnoty je ve tvaru S-Křivky). V takovém systému proměnná nejdříve exponenciálně roste díky vlivu pozitivní zpětnovazební smyčky. Její růst je ale limitován negativní zpětnovazební smyčkou, která určuje maximální možnou hodnotu, na kterou se může hodnota elementu dostat.

Cld behaviour sshape.png

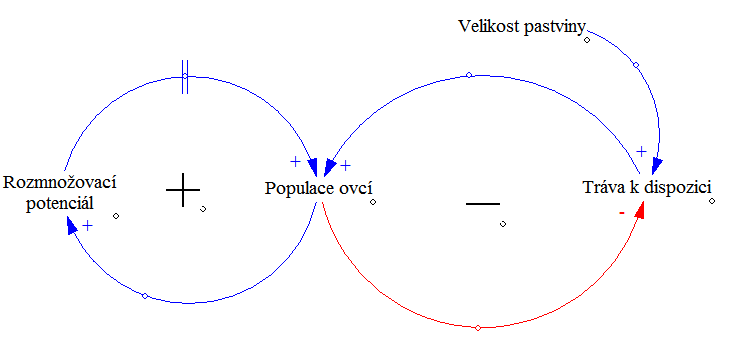
Toto chování si ukážeme na příkladu populace ovcí, který žije na pastvině s omezeným zdrojem potravy. Množství trávy na pastvině je dané její velikostí. Ze začátku populace ovcí roste exponenciálně, protože její velikost je daleko od limitu, který je dán množstvím trávy na pastvině. Ve chvíli, kdy rostoucí populace ovcí začne spásat trávu rychleji, než stačí dorůstat nová, tak se růst populace postupně spomalí dokud se neustálí na maximální možné výši.


Cld diagram sheep.png

Skoro každý exponenciální růst v dynamickém systému nakonec narazí na nějaký limit daný negativní zpětnovazební smyčkou. Růst organizace, růst prodejů nebo růst populací jsou typickými příklady tohoto chování.

Postup tvorby diagramu kauzálních smyček

Na začátku tvorby diagramu kauzálních smyček, se nejdříve zkuste zamyslet, jaké kvantifikovatelné ukazatele/objekty systému jsou pro vás zajímavé a jaké události jsou významné pro pochopení struktury a chování modelu. Pokud například vytváříte diagram zachycující dynamiku efektivity prodejního oddělení, tak pravděpodobně budete chtít váš diagram postavit kolem ukazatele měsíční prodeje a budete hledat události, které ho ovlivňují. Pokuste si uvědomit, jak se hodnota ukazatele, o který se zajímáte vyvíjí v čase. Roste exponenciálně? Osciluje? Růst se zpomaluje (S-Křivka)? Ve chvíli, kdy znáte hlavní objekt/ukazatel systému, o který se zajímate, znáte události, který na něj mají vliv a uvědomujete si průběh vývoje jeho hodnoty, můžete přistoupit k tvorbě diagramu za pomocí kombinací základních typů kauzálních smyček, které dohromady vysvětlí jeho chování.

Postup tvorby diagramu může být následující [6]:

  1. Přemýšlejte o elementech diagramu jako o proměnných, které mohou nárůstat nebo klesat. Nelámejte si hlavu s tím, pokud pro ně nedokážete určit jednotku nebo měřítko. Zakreslete do diagramu proměnnou, která vás nejvíce zajímá a postupně k ní dokreslete ostatní proměnné, které její stav ovlivňují.
    • Jako název proměnné (elementu) používejte raději podstatné jméno, nežli sloveso. Nárůst/pokles (tedy určitá akce) těchto proměnných je potom vyjádřena šipkami. Proto například "cena" je vhodnější název pro proměnnou, než "zvyšující se cena".
    • Ujistěte se, že je jasné z názvu proměnné, kterým směrem se její hodnota zvyšuje. Je lepší použít název proměnné "tolerance xenofobie ve společnosti" namísto "názor na xenofobii ve společnosti"
    • Obecně je lepší používat takové názvy proměnných, které jsou pozitivní a naznačují přibývání veličiny. Je preferováno nazvat proměnou "rychlost růstu" než-li "rychlost zmenšování"
    • Šipky mezi proměnnými by měli nést význam kauzality a ne pohé časové souslednosti. Šipka od proměnné A k proměnné B neznamené "nejdřív proběhne A, potom B". Význam takového spojení je "Pokud vzroste A, vzroste i B"
  2. Jak budete postupně vytvářet diagram, zkuste se zamyslet nad nežádoucími vedlejšími účinky, které mohou nastat ve vašem diagramu. Pokud na nějakou interakci tohoto typu přidejte, zakreslete do diagramu příslušná propojení šipkami, abyste zachytili vliv tohoto jevu.
  3. Negativní zpětné smyčky mají cílový stav, ke kterému se proměnné ve smyčce přibližují. Je obvykle lepší pro větší přehlednost hodnotu cílového stavu do diagramu zanést společně s proměnnou, která reprezentuje rozdíl, který ještě zbývá k dosažení této cílové hodnoty.
  4. Rozdíl mezi skutečnou a vnímanou hodnotou elemetnu procesu může být důležitý pro vysvětlení vzorců chování systému. Proto je v některých případech důležité zavést do diagramu zvlášť proměnnou jak pro vnímanou tak pro skutečnou hodnotu. Obzvláště to platí v modelování systémů, kde mezi změnou skutečné hodnoty a jejím vnímatelným projevem existuje zpoždění.
  5. Obvykle existuje rozdíl mezi krátkodobými a dlouhodobými dopady určité akce a proto je potřeba je pro ně vytvořit oddělené kauzální smyčky. Například při požití léku upravující náladu se pacient v krátkodobém horizontu cítí lépe. V dlouhodobém měřítku však může riskovat závislost na léčivu a zhoršení zdravotního stavu.
  6. Pokud šipka mezi dvěma elementy vyžaduje mnoho vysvětlování, pravděpodobně by bylo vhodné přidat mezi již existující proměnné další element, který osvětlí, co se v systému děje.
  7. Snažte se diagram držet co nejjednodušší (při dodržení výše uvedených bodů). Účel diagramu není popsat každý detail zvoleného procesu v systému ale spíše ukázat podstatné aspekty struktury zpětné vazby, které způsobují pozorované chování elementů (proměnných) v systému.

VenSim - Nástroj pro vytváření diagramů kauzálních smyček

Uživatelské rozhraní nástroje VenSim

Jedním z nástrojů, který lze použít k modelování diagramů kauzálních smyček je nástroj VenSim, který je zdarma dostupný pro nekomerční použití. VenSim lze stáhnout z oficiální stránky jeho výrobce. Kromě vytváření diagramů kauzálních smyček umožňuje tento nástroj tvorbu Stock And Flow Diagramů. Umožňuje simulaci vytvořených modelů, generování stomů příčin a následků a identifikaci zpětnovazebních smyček.[7]:

Příklady k procvičení

U následujících diagramů určete, zda chování jejich hodnot bude vykazovat exponenciální růst, hledání hodnoty, oscilace nebo S-Křivku:

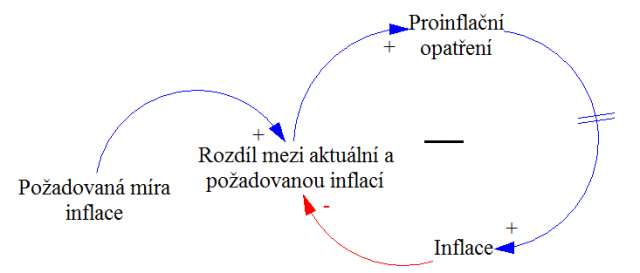
a) Protinflační opatření ČNB:

Intervence ČNB


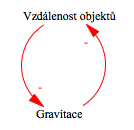
b) Gravitace

Cld ex1 pos feed2.png


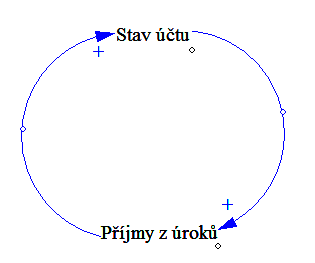
c) Bankovní účet

Cld ex1 pos feed.png


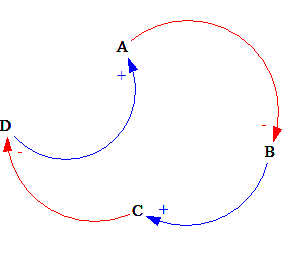
d) Generický diagram (Určete chování proměnné A)

Cld ex1 neg.png


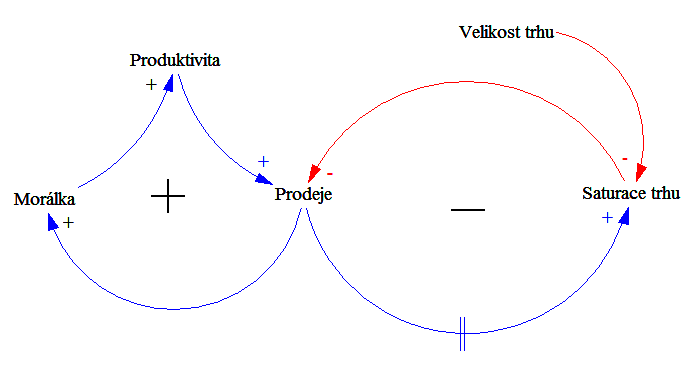
e) Vývoj prodejů (určete chování proměnné Prodeje)

Cld ex1 sshape.png


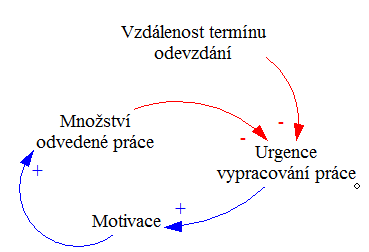
f) Studentský syndrom

Cld ex1 neg2.png


Řešení: a)Oscilace b)Exponenciální růst c)Exponenciální růst d)Exponenciální růst e)S-Křivka f) Hledání hodnoty

Reference

  1. ↑ Hayward J., Introduction To System Dynamics [online]. [cit. 2013-06-15]. Dostupné z: http://www.churchmodel.org.uk/introsystems.pdf
  2. ↑ North K., An Introduction to Systems Thinking - How to Read Causal Loop Diagrams (CLDs) [online]. [cit. 2013-06-17]. Dostupné z: http://courses.umass.edu/plnt597s/KarlsArticle.pdf
  3. ↑ Kirkwood, System Behavior and Causal LoopDiagrams, Chapter 1 [online]. [cit. 2013-06-15]. Dostupné z: http://www.public.asu.edu/~kirkwood/sysdyn/SDIntro/ch-1.pdf
  4. ↑ Kirkwood, System Behavior and Causal LoopDiagrams, 1.4 System Structure and Patterns of Behavior [online]. [cit. 2013-06-15]. Dostupné z: http://www.public.asu.edu/~kirkwood/sysdyn/SDIntro/ch-1.pdf
  5. ↑ Kirkwood, System Behavior and Causal LoopDiagrams, 1.3 Feedback and Causal Loop Diagrams [online]. [cit. 2013-06-15]. Dostupné z: http://www.public.asu.edu/~kirkwood/sysdyn/SDIntro/ch-1.pdf
  6. ↑ Kirkwood, System Behavior and Causal LoopDiagrams, 1.5 Creating Causal Loop Diagrams [online]. [cit. 2013-06-15]. Dostupné z: http://www.public.asu.edu/~kirkwood/sysdyn/SDIntro/ch-1.pdf
  7. ↑ VenSim, Vensim Software [online]. [cit. 2013-06-17]. Dostupné z: http://vensim.com/vensim-software/
Retrieved from "http://www.simulace.info/index.php?title=Causal_Loop_Diagram/cs&oldid=7382"