Difference between revisions of "General Behavior of Infections"
(→How does it work?) |
|||
| (52 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
=Problem definition= | =Problem definition= | ||
| + | My semestral paper was on visualization of disease and it´s spreading amongst population. Although there are many models available, most of them are quite straightforward and very simple. Mostly they are concentrating on spreading the disease itself, without any thought placed into the surrounding environment, like spread of the people. I tried to make the whole system more complex by adding some basic behavior to the agents as well as more variables, by which is the infection defined. This creates a more complex insight into the way of spreading infections. At least to better extend than most models. The model and it´s interface is also designed for easy use and allow users change variables easily. | ||
| + | |||
| + | Note: I have do add, that the model is far from my liking actually. It still lacks complexity I would like to see and implement. That is partly due to problem with speed. Although simulating 10 000 agents with relatively simple behavior is possible, by adding more and more complex behavior, the whole system started to slow down considerably (I ended with one tick per 30 seconds which is not exactly ideal state for simulating). | ||
=Method= | =Method= | ||
| + | For my model of visualization, how diseases spread, I have chosen Netlogo as a tool, as it allows to play with all the values quite easily and reward the user with nice visualization of the whole situation, as well as giving enough data from various graphs and is robust enough, for simulating various relatively complex behavior. | ||
| − | = | + | =How does it work?= |
| − | Agents: People | + | There are two main modules. One take care of logic behind moving of agents and the other one is for infection spread. Although for easier navigation they are split into more files. |
| + | The whole model consist of breed of agents called people. Space is 501 on 501 squares (patches). Number of agent is variable. Patches have attributes, that tells agent, if they are inside city, village or out in country side. When people are spread, most of them is located inside cities, while is or is not present inside villages. Smaller portion of people are distributed randomly in country side. People have various decisions how to move. Mostly they move around in either country side, villages or cities. When they are in city, there is very big chance, that they stay inside the city. This simulates behavior, that we stay inside city, work and live here and occasionally venture out. Same goes for villages, but to a smaller degree, as the size of villages are smaller. Once in a while (when WILL to go out is bigger than randomly generated number), agent venture out to a randomly generated coordination. After he reaches it, he goes via the shortest way back where he came from. If disease is curable, the is marginally bigger chance of curing it inside city and slightly bigger in villages. In country, as there are no hospitals, chance of being cured is actually a lot smaller, than of that, which is set in interface. At the start, each of peoples have set, if he is infected or not. If he is, and he is contagious, he can spread disease and those near him may catch the disease. The exact way the disease work is following. First, people catch disease. At that moment, they may enter incubation period for which he is infected, but he cannot infect others. After certain period, he become contagious. Next step is that the disease became known to it´s surrounding. But until it is known, that person is infected, he cannot be cured. When certain amount of time passes and he was not cured, he will either die of disease or he may have constitution good enough, and he survives the disease. Surviving disease is equivalent to being cured. It may or may not give that person immunity. | ||
| + | ---- | ||
| + | |||
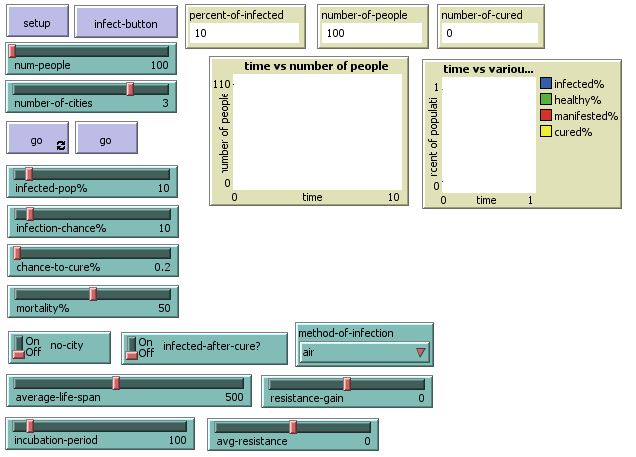
| + | So, how does it all work and who does all those buttons do? It all looks like this.<div> | ||
| + | [[File:Xvism00_interfaceJPG.JPG]] | ||
| + | <div> | ||
| + | BUTTONS: | ||
| + | *SETUP – set up whole model. Meaning people and surrounding. | ||
| + | *GO (infinite) – to run model indefinitely. | ||
| + | *GO(once) – to advance by one tick. | ||
| + | *INFECT-BUTTON – button infect one random agent, who is not infected. | ||
| + | <div> | ||
| + | SWITCHES and CHOOSERS: | ||
| + | *NO-CITY - when SETUP is pressed, space is void of cities and villages. This is how most other infection models work and it´s implemented for comparison with other models although agents lacks thanks to this some more advanced behavior. This switch override NUMBER-OF-CITIES slider. Meaning it is not important, how many cities you have chosen to spawn as long as the switch is in ON position. | ||
| + | *INFECTED-AFTER-CURE? - If people can be infected, after they are cured from the disease. Setting the switch to position OFF means, that once agent is cured, he cannot catch the disease again, making him totally immune. | ||
| + | *METHOD-OF-INFECTION - chooses by which method is the disease spread. Either by AIR (which is more effective) or by BODY-CONTACT, which is not se effective in spreading. | ||
| + | <div> | ||
| + | SLIDERS: | ||
| + | *NUM-PEOPLE – total number of people created at setup. | ||
| + | *NUMBER-OF-CITIES – number of cities created, which are then randomly spread around the field. The can be connected and theoreticaly emerge at the same location. Although given the number of patches, it is very unlikely. Size of each city can vary slightly due to random element (random-normal 500 200). | ||
| + | *INFECTED-POP% - percent of population already infected at the creation of space. | ||
| + | *INFECTION-CHANCE% - chance of spreading disease in percents. Note, that this is ONLY for rough value. Catching disease is randomized and more complex. | ||
| + | *CHANCE-TO-CURE% - chance to be cured, after the disease make itself known to surrounding. In percents. | ||
| + | *MORTALITY% - chance that disease will kill infected. | ||
| + | *AVERAGE-LIFE-SPAN – average time for each agent, after being infected, to see, if he dies or survives. Each agent life span is calculated by (random-normal average-life-span 100). | ||
| + | *INCUBATION-PERIOD – average time after agent is infected but does not infect other agents. Again, it is individualy calculated using random normal distribution. | ||
| + | *RESISTANCE-GAIN - each time agent get cured, he gain this amount to his resistance roll, so next time, he resist the disease better. | ||
| + | *AVG-RESISTANCE - average value which each agent is given at his setup. If set at 0, each agent has value starting with 0. | ||
| + | ---- | ||
| + | Agents (people) | ||
| + | <div> | ||
| + | The agents, here represented by people, have various attributes, which we will now explain. | ||
| + | *infected? - (T/F) - Depending, if he is infected. | ||
| + | * contagious? - (T/F) - If T, he can infect people around him. | ||
| + | * manifested? - (T/F) - If T, he know about his condition, that he has disease and he can start curing it. | ||
| + | * infection-length - (number) - Each agent have number of ticks, for which he is infected. | ||
| + | * cured? - (T/F) - T if he was infected but either cured or after he survived the disease. | ||
| + | * incubation-length - (number) - How long will stay the disease lay dormant after agent is infected by it. | ||
| + | * life-span - (number) - How long will it take, before it is decided, if he dies by disease or survives it. | ||
| + | * resistance - (number) - Number, that is added to chance of catching disease. Can be negative (more easily catch disease) or positive, for strengthened survivability. | ||
| + | |||
| + | * where-to-x - (coordinates in space) - X coordination, where the agent wants to go next. | ||
| + | * where-to-y - same as above, only for Y. | ||
| + | * origin-x - (coordinates in space) - When agent sets on a trip, he saves value from which he departed. | ||
| + | * origin-y - same as above, only for Y. | ||
| + | * wait-time - (number) - how long since last trip. The higher the bigger chance, that he will go out. | ||
| + | * will - (number) - how often will agent go out for a trip. The lower the more often he will go out. | ||
| + | <div> | ||
| + | ----- | ||
| + | [[Image:Obr_plocha1.jpg|center|thumb|400px|Space]] | ||
| + | This is example, how does the space created looks like. Cities are grey and have a random size. Villages are white-grey. Green is country side. At start, people are concentrated in the cities. Even throughout the simulation people concentrate in the cities despite venturing occasionally out. | ||
| + | <div> | ||
| + | Aside from those values, agents also change color accordingly to they´re current status. White is not infected, cyan if infected but still not contagious, yellow when the incubation period cease and he became contagious and red, when the disease manifest itself. Number of agents is set via user interface. There is also global variable, which is chance to infect. | ||
| + | |||
| + | ---- | ||
| + | Model limitation and possible expansions. | ||
| + | <div> | ||
| + | The model is far from flawless. It is still a model. Many features are not implemented because of hardware problem (one tick per 30 second is not exactly fast), but some I retained inside the netlogo code for future use and expansions. So, what are the limitations? People does not act as in real life. There are no cars, no roads that make the travel faster and allow for bigger concentration of people on they way between cities. Disease is also quite limited. People don´t die by age, as model is not targeted on so long time. | ||
| + | <div> | ||
| + | Idea for making the model better? I would implement fear factor. When population start dying at certain rate or slowly reaches some level, people will start to act differently. If the disease start to spread, the martial law could be declared, meaning that cities will get quarantined. Also it would be nice to see the disease in longer time. When people start to die and new are born and that the disease could be transferred from mother to child. Another idea is mutation of virus. All those ideas are relatively easily implementable. | ||
=Results= | =Results= | ||
| + | There are many attributes and their combination, which can be selected as means for obtaining relevant data. How many people are being cured, how many died and so on. It is also quite In my results I focused on how many people survived and how effective was the disease, meaning how many people were infected in a limited time window, when those attributes are changing: | ||
| + | <div> | ||
| + | *INFECTION-CHANCE | ||
| + | *CHANCE-TO-CURE | ||
| + | *AVG-RESISTANCE | ||
| + | *MORTALITY | ||
| + | *RESISTANCE-GAIN | ||
| + | *AVERAGE-LIFE-SPAN | ||
| + | *NUMBER-OF-PEOPLE | ||
| + | <DIV> | ||
| + | I created two behavioral spaces with different sets of parameters. For both runs there were 3 cities and people cut get infected again, after they have been cured. Infected population was 10% and in both cases method of spreading the disease was via air. Also the incubation of disease was random-normal 100 for both scenarios. It should be noted, that thanks to quite a large number of variables, most of them with slider settings, running a thorough test would take long time, so I chose those variables, which I deemed fit for my goal. Now, the first run. | ||
| + | <div> | ||
| + | First set of rules was following: | ||
| + | <div> | ||
| + | :["no-city" false] | ||
| + | :["infected-after-cure?" true] | ||
| + | :["infection-chance%" 10 50 75] | ||
| + | :["chance-to-cure%" 0.1 1 5] | ||
| + | :["avg-resistance" 0 40] | ||
| + | :["number-of-cities" 3] | ||
| + | :["infected-pop%" 10] | ||
| + | :["incubation-period" 100] | ||
| + | :["average-life-span" 500] | ||
| + | :["num-people" 2000] | ||
| + | :["method-of-infection" "air"] | ||
| + | :["mortality%" 0 1 10] | ||
| + | :["resistance-gain" 0] | ||
| + | <div> | ||
| + | This is the setting for first set of runs. There were 64 combinations which were each ran 4times. Although that may seem like a small numbers, it was quite enough, as all 4 runs are in virtually all cases very near to each other (but not always). That is due to 2000 agents, which smooth up any irregularities, like a bigger number of runs would. Reason for this is hardware. Each run, even with limit of 2000 ticks, ran for around one minute. I have chosen 2000 ticks as this amount of time was mostly adequate. In most cases, according to graphs, nothing new and interesting emerges after that time span and the trend was linear. So whoever had highest value od death in 2000, would have so in 4000 ticks. | ||
| + | |||
| + | Killer disease | ||
| + | <div> | ||
| + | The "winning" combination for most effective killer disease was no surprise. Biggest spread and biggest chance for dying after being infected 75% and 10% respectively). The "best" diseases can wipe out nearly quarter of population (484 agents) in a time span of 2000 ticks. But at that time, there were still 1221 people infected, who could die. (The rate at which people died was statistically around 50 people per 200 ticks and was virtually linear.) So the disease was still spreading. But there are some nice conclusions from data. For example, having infection chance of 50% and average resistance of 40% is equivalent to infection chance of 10% and average resistance 0%. Although not nearly identical, resistance is roughly equal of lowering infection chance by the same amount. But not quite. There can be identified leverage points in mortality and also chance of getting cured. Chance of being infected is quite unimportant for maximal death ratio. While logically for most infected, the mortality is required to be as low as possible, since if people dies, we don´t have that many infected. | ||
| + | But, if we have chance to cure of 5% and average resistance 40% combined with 10% infection ration and 1% death rate, surprisingly, no one dies. The same goes for 50% infection. | ||
| + | <div> | ||
| + | Most annoying caught | ||
| + | <div> | ||
| + | Here, the goal was to infect as many people as possible. For measuring, the most important is mean number of infected people. The higher, the better. Why we cannot use final value of infected? Because, as we can see in included excel, if we sort values by final value of infected, mean is sometimes lower and sometimes bigger. Reason behind this is that never does any disease infect all people. In remote location of country, of cities, people are very hard to get infected. And number of disease people, since they can get cured, can in one moment be lower or higher than in others. | ||
| + | Interestingly, if we have chance to cure of 5% and average resistance 40% combined with 10% infection ration and 1% death rate (no deaths), that the number of infected people, under those values, vary very much. Once there are 57 infected at 2000 ticks and in second run with same values, there are 800 infected. But it have to be said, that this is very extreme example. The biggest values are archieved have the highest value for spreading and lowest chance to cure with no mortality. | ||
| + | And which are the most ineffective combinations? They are those, with high chance to kill infected, but small chance with spreading. | ||
| + | <div> | ||
| + | |||
| + | Second one have had those attributes and variables set: | ||
| + | <div> | ||
| + | :["no-city" false] | ||
| + | :["infected-after-cure?" true] | ||
| + | :["infection-chance%" 100] | ||
| + | :["chance-to-cure%" 0.1 0.3 0.8] | ||
| + | :["avg-resistance" 0 80] | ||
| + | :["number-of-cities" 3] | ||
| + | :["infected-pop%" 10] | ||
| + | :["incubation-period" 100] | ||
| + | :["average-life-span" 100] | ||
| + | :["num-people" 1000] | ||
| + | :["method-of-infection" "air"] | ||
| + | :["mortality%" 0 1 10] | ||
| + | :["resistance-gain" 5] | ||
| + | <div> | ||
| + | Second set of runs war with 18 variation. Each one 8 times with the same settings. This number was unnecessary high, as 4 would suffice. The second set, despite bigger infection chance, was not as effective as the first batch. Over third of all runs had no infected at the end. | ||
| + | Killer disease | ||
| + | <div> | ||
| + | The amount of deceased is quite similar with the first batch, in case of "winners". Around one third died. Unlike the first batch, there were very few infected to continue with dying. Some actually run out of infected people altogether. (I disregarded some runs for reasons below.) Surprisingly, chance to cure the disease did little to the amount of death. That is probably again due to the already mentioned phenomenon. But here, the least successful killers are those, without killing power. There is no one with chance to kill among those. Anyone, with some mortality, kill someone. Unlikely the first batch. | ||
| + | <div> | ||
| + | Most annoying caught | ||
| + | <div> | ||
| + | Those worst killers are on the other hand the best infectioners. With nearly 98% infected people. That is very high marks. Second is actually slow killer. They have mortality 1% and, they have much more infected than runs with exactly the same setting, but without mortality. They have around 200 more infected, than those with mortality 0. That is quite unexpected. The losers on the other hand are expected. But what is interesting, that average resistance have no effect on final number of infected people. They all have 0 infected and mean identical, so they cured at roughly the same time. | ||
| + | <div> | ||
| + | For some reason, unknown to me, runs 17 to 24 have higher number of infected people than there are people alive. Only those eight sets of runs and my tries to replicate those values yielded nothing. I ran the model with the same values 10 times and never had I more infected than living. I changed a code little bit since then, so it is possible, it was some wrong code. But now it works fine. I disregarded those values. | ||
| + | <div> | ||
| + | |||
| + | Exact results and data can be found in excel files, which I have transformed for easy use and simple orientation and for easy way to obtain necessary results. | ||
=Conclusion= | =Conclusion= | ||
| + | What is there to conclude? | ||
| + | *The amount of people shows slightly bigger extremes in values, like we can see it second batch. It seem, that those extremes are due to the lower number of people. Also, not surprisingly, if we want to spread disease, the bigger the chance to catch it, the better (for the disease, not for the person who catch it). The worst situation is inside and near the cities, where there is bigger concentration of people on the same size of land, than in villages or country side. | ||
| + | *The chance of getting cured is not as important, as it may seem. While it is of course very important, tripling the value does not do much in terms of lowering number of deceased. Why is that? Since disease can be cured only when it manifest itself, so that person know, he should start treating himself, it could leave relatively small time window for him, to get cured. Sometimes, symptoms manifested themselves few ticks before he dies, so small increment in chance of getting cure is not having that much of an impact. On the other hand, chance of getting cured is essential in number of people, who are infected. The higher the number, the lower the number of infected people. | ||
| + | *Spreading of disease is relatively predictable after certain time, when it stabilizes. | ||
| + | *Given enough time, few diseases would be able to actually infect everyone, but none would be able to kill everyone unless set at extreme values. | ||
| − | = | + | =Files= |
| + | [[Media:GDV.zip]] | ||
| + | [[Media:Results_of_runs.xlsx]] | ||
Latest revision as of 21:37, 15 January 2014
Introduction
Problem definition
My semestral paper was on visualization of disease and it´s spreading amongst population. Although there are many models available, most of them are quite straightforward and very simple. Mostly they are concentrating on spreading the disease itself, without any thought placed into the surrounding environment, like spread of the people. I tried to make the whole system more complex by adding some basic behavior to the agents as well as more variables, by which is the infection defined. This creates a more complex insight into the way of spreading infections. At least to better extend than most models. The model and it´s interface is also designed for easy use and allow users change variables easily.
Note: I have do add, that the model is far from my liking actually. It still lacks complexity I would like to see and implement. That is partly due to problem with speed. Although simulating 10 000 agents with relatively simple behavior is possible, by adding more and more complex behavior, the whole system started to slow down considerably (I ended with one tick per 30 seconds which is not exactly ideal state for simulating).
Method
For my model of visualization, how diseases spread, I have chosen Netlogo as a tool, as it allows to play with all the values quite easily and reward the user with nice visualization of the whole situation, as well as giving enough data from various graphs and is robust enough, for simulating various relatively complex behavior.
How does it work?
There are two main modules. One take care of logic behind moving of agents and the other one is for infection spread. Although for easier navigation they are split into more files. The whole model consist of breed of agents called people. Space is 501 on 501 squares (patches). Number of agent is variable. Patches have attributes, that tells agent, if they are inside city, village or out in country side. When people are spread, most of them is located inside cities, while is or is not present inside villages. Smaller portion of people are distributed randomly in country side. People have various decisions how to move. Mostly they move around in either country side, villages or cities. When they are in city, there is very big chance, that they stay inside the city. This simulates behavior, that we stay inside city, work and live here and occasionally venture out. Same goes for villages, but to a smaller degree, as the size of villages are smaller. Once in a while (when WILL to go out is bigger than randomly generated number), agent venture out to a randomly generated coordination. After he reaches it, he goes via the shortest way back where he came from. If disease is curable, the is marginally bigger chance of curing it inside city and slightly bigger in villages. In country, as there are no hospitals, chance of being cured is actually a lot smaller, than of that, which is set in interface. At the start, each of peoples have set, if he is infected or not. If he is, and he is contagious, he can spread disease and those near him may catch the disease. The exact way the disease work is following. First, people catch disease. At that moment, they may enter incubation period for which he is infected, but he cannot infect others. After certain period, he become contagious. Next step is that the disease became known to it´s surrounding. But until it is known, that person is infected, he cannot be cured. When certain amount of time passes and he was not cured, he will either die of disease or he may have constitution good enough, and he survives the disease. Surviving disease is equivalent to being cured. It may or may not give that person immunity.
So, how does it all work and who does all those buttons do? It all looks like this.
BUTTONS:
- SETUP – set up whole model. Meaning people and surrounding.
- GO (infinite) – to run model indefinitely.
- GO(once) – to advance by one tick.
- INFECT-BUTTON – button infect one random agent, who is not infected.
SWITCHES and CHOOSERS:
- NO-CITY - when SETUP is pressed, space is void of cities and villages. This is how most other infection models work and it´s implemented for comparison with other models although agents lacks thanks to this some more advanced behavior. This switch override NUMBER-OF-CITIES slider. Meaning it is not important, how many cities you have chosen to spawn as long as the switch is in ON position.
- INFECTED-AFTER-CURE? - If people can be infected, after they are cured from the disease. Setting the switch to position OFF means, that once agent is cured, he cannot catch the disease again, making him totally immune.
- METHOD-OF-INFECTION - chooses by which method is the disease spread. Either by AIR (which is more effective) or by BODY-CONTACT, which is not se effective in spreading.
SLIDERS:
- NUM-PEOPLE – total number of people created at setup.
- NUMBER-OF-CITIES – number of cities created, which are then randomly spread around the field. The can be connected and theoreticaly emerge at the same location. Although given the number of patches, it is very unlikely. Size of each city can vary slightly due to random element (random-normal 500 200).
- INFECTED-POP% - percent of population already infected at the creation of space.
- INFECTION-CHANCE% - chance of spreading disease in percents. Note, that this is ONLY for rough value. Catching disease is randomized and more complex.
- CHANCE-TO-CURE% - chance to be cured, after the disease make itself known to surrounding. In percents.
- MORTALITY% - chance that disease will kill infected.
- AVERAGE-LIFE-SPAN – average time for each agent, after being infected, to see, if he dies or survives. Each agent life span is calculated by (random-normal average-life-span 100).
- INCUBATION-PERIOD – average time after agent is infected but does not infect other agents. Again, it is individualy calculated using random normal distribution.
- RESISTANCE-GAIN - each time agent get cured, he gain this amount to his resistance roll, so next time, he resist the disease better.
- AVG-RESISTANCE - average value which each agent is given at his setup. If set at 0, each agent has value starting with 0.
Agents (people)
The agents, here represented by people, have various attributes, which we will now explain.
- infected? - (T/F) - Depending, if he is infected.
- contagious? - (T/F) - If T, he can infect people around him.
- manifested? - (T/F) - If T, he know about his condition, that he has disease and he can start curing it.
- infection-length - (number) - Each agent have number of ticks, for which he is infected.
- cured? - (T/F) - T if he was infected but either cured or after he survived the disease.
- incubation-length - (number) - How long will stay the disease lay dormant after agent is infected by it.
- life-span - (number) - How long will it take, before it is decided, if he dies by disease or survives it.
- resistance - (number) - Number, that is added to chance of catching disease. Can be negative (more easily catch disease) or positive, for strengthened survivability.
- where-to-x - (coordinates in space) - X coordination, where the agent wants to go next.
- where-to-y - same as above, only for Y.
- origin-x - (coordinates in space) - When agent sets on a trip, he saves value from which he departed.
- origin-y - same as above, only for Y.
- wait-time - (number) - how long since last trip. The higher the bigger chance, that he will go out.
- will - (number) - how often will agent go out for a trip. The lower the more often he will go out.
This is example, how does the space created looks like. Cities are grey and have a random size. Villages are white-grey. Green is country side. At start, people are concentrated in the cities. Even throughout the simulation people concentrate in the cities despite venturing occasionally out.
Aside from those values, agents also change color accordingly to they´re current status. White is not infected, cyan if infected but still not contagious, yellow when the incubation period cease and he became contagious and red, when the disease manifest itself. Number of agents is set via user interface. There is also global variable, which is chance to infect.
Model limitation and possible expansions.
The model is far from flawless. It is still a model. Many features are not implemented because of hardware problem (one tick per 30 second is not exactly fast), but some I retained inside the netlogo code for future use and expansions. So, what are the limitations? People does not act as in real life. There are no cars, no roads that make the travel faster and allow for bigger concentration of people on they way between cities. Disease is also quite limited. People don´t die by age, as model is not targeted on so long time.
Idea for making the model better? I would implement fear factor. When population start dying at certain rate or slowly reaches some level, people will start to act differently. If the disease start to spread, the martial law could be declared, meaning that cities will get quarantined. Also it would be nice to see the disease in longer time. When people start to die and new are born and that the disease could be transferred from mother to child. Another idea is mutation of virus. All those ideas are relatively easily implementable.
Results
There are many attributes and their combination, which can be selected as means for obtaining relevant data. How many people are being cured, how many died and so on. It is also quite In my results I focused on how many people survived and how effective was the disease, meaning how many people were infected in a limited time window, when those attributes are changing:
- INFECTION-CHANCE
- CHANCE-TO-CURE
- AVG-RESISTANCE
- MORTALITY
- RESISTANCE-GAIN
- AVERAGE-LIFE-SPAN
- NUMBER-OF-PEOPLE
I created two behavioral spaces with different sets of parameters. For both runs there were 3 cities and people cut get infected again, after they have been cured. Infected population was 10% and in both cases method of spreading the disease was via air. Also the incubation of disease was random-normal 100 for both scenarios. It should be noted, that thanks to quite a large number of variables, most of them with slider settings, running a thorough test would take long time, so I chose those variables, which I deemed fit for my goal. Now, the first run.
First set of rules was following:
- ["no-city" false]
- ["infected-after-cure?" true]
- ["infection-chance%" 10 50 75]
- ["chance-to-cure%" 0.1 1 5]
- ["avg-resistance" 0 40]
- ["number-of-cities" 3]
- ["infected-pop%" 10]
- ["incubation-period" 100]
- ["average-life-span" 500]
- ["num-people" 2000]
- ["method-of-infection" "air"]
- ["mortality%" 0 1 10]
- ["resistance-gain" 0]
This is the setting for first set of runs. There were 64 combinations which were each ran 4times. Although that may seem like a small numbers, it was quite enough, as all 4 runs are in virtually all cases very near to each other (but not always). That is due to 2000 agents, which smooth up any irregularities, like a bigger number of runs would. Reason for this is hardware. Each run, even with limit of 2000 ticks, ran for around one minute. I have chosen 2000 ticks as this amount of time was mostly adequate. In most cases, according to graphs, nothing new and interesting emerges after that time span and the trend was linear. So whoever had highest value od death in 2000, would have so in 4000 ticks.
Killer disease
The "winning" combination for most effective killer disease was no surprise. Biggest spread and biggest chance for dying after being infected 75% and 10% respectively). The "best" diseases can wipe out nearly quarter of population (484 agents) in a time span of 2000 ticks. But at that time, there were still 1221 people infected, who could die. (The rate at which people died was statistically around 50 people per 200 ticks and was virtually linear.) So the disease was still spreading. But there are some nice conclusions from data. For example, having infection chance of 50% and average resistance of 40% is equivalent to infection chance of 10% and average resistance 0%. Although not nearly identical, resistance is roughly equal of lowering infection chance by the same amount. But not quite. There can be identified leverage points in mortality and also chance of getting cured. Chance of being infected is quite unimportant for maximal death ratio. While logically for most infected, the mortality is required to be as low as possible, since if people dies, we don´t have that many infected. But, if we have chance to cure of 5% and average resistance 40% combined with 10% infection ration and 1% death rate, surprisingly, no one dies. The same goes for 50% infection.
Most annoying caught
Here, the goal was to infect as many people as possible. For measuring, the most important is mean number of infected people. The higher, the better. Why we cannot use final value of infected? Because, as we can see in included excel, if we sort values by final value of infected, mean is sometimes lower and sometimes bigger. Reason behind this is that never does any disease infect all people. In remote location of country, of cities, people are very hard to get infected. And number of disease people, since they can get cured, can in one moment be lower or higher than in others. Interestingly, if we have chance to cure of 5% and average resistance 40% combined with 10% infection ration and 1% death rate (no deaths), that the number of infected people, under those values, vary very much. Once there are 57 infected at 2000 ticks and in second run with same values, there are 800 infected. But it have to be said, that this is very extreme example. The biggest values are archieved have the highest value for spreading and lowest chance to cure with no mortality. And which are the most ineffective combinations? They are those, with high chance to kill infected, but small chance with spreading.
Second one have had those attributes and variables set:
- ["no-city" false]
- ["infected-after-cure?" true]
- ["infection-chance%" 100]
- ["chance-to-cure%" 0.1 0.3 0.8]
- ["avg-resistance" 0 80]
- ["number-of-cities" 3]
- ["infected-pop%" 10]
- ["incubation-period" 100]
- ["average-life-span" 100]
- ["num-people" 1000]
- ["method-of-infection" "air"]
- ["mortality%" 0 1 10]
- ["resistance-gain" 5]
Second set of runs war with 18 variation. Each one 8 times with the same settings. This number was unnecessary high, as 4 would suffice. The second set, despite bigger infection chance, was not as effective as the first batch. Over third of all runs had no infected at the end. Killer disease
The amount of deceased is quite similar with the first batch, in case of "winners". Around one third died. Unlike the first batch, there were very few infected to continue with dying. Some actually run out of infected people altogether. (I disregarded some runs for reasons below.) Surprisingly, chance to cure the disease did little to the amount of death. That is probably again due to the already mentioned phenomenon. But here, the least successful killers are those, without killing power. There is no one with chance to kill among those. Anyone, with some mortality, kill someone. Unlikely the first batch.
Most annoying caught
Those worst killers are on the other hand the best infectioners. With nearly 98% infected people. That is very high marks. Second is actually slow killer. They have mortality 1% and, they have much more infected than runs with exactly the same setting, but without mortality. They have around 200 more infected, than those with mortality 0. That is quite unexpected. The losers on the other hand are expected. But what is interesting, that average resistance have no effect on final number of infected people. They all have 0 infected and mean identical, so they cured at roughly the same time.
For some reason, unknown to me, runs 17 to 24 have higher number of infected people than there are people alive. Only those eight sets of runs and my tries to replicate those values yielded nothing. I ran the model with the same values 10 times and never had I more infected than living. I changed a code little bit since then, so it is possible, it was some wrong code. But now it works fine. I disregarded those values.
Exact results and data can be found in excel files, which I have transformed for easy use and simple orientation and for easy way to obtain necessary results.
Conclusion
What is there to conclude?
- The amount of people shows slightly bigger extremes in values, like we can see it second batch. It seem, that those extremes are due to the lower number of people. Also, not surprisingly, if we want to spread disease, the bigger the chance to catch it, the better (for the disease, not for the person who catch it). The worst situation is inside and near the cities, where there is bigger concentration of people on the same size of land, than in villages or country side.
- The chance of getting cured is not as important, as it may seem. While it is of course very important, tripling the value does not do much in terms of lowering number of deceased. Why is that? Since disease can be cured only when it manifest itself, so that person know, he should start treating himself, it could leave relatively small time window for him, to get cured. Sometimes, symptoms manifested themselves few ticks before he dies, so small increment in chance of getting cure is not having that much of an impact. On the other hand, chance of getting cured is essential in number of people, who are infected. The higher the number, the lower the number of infected people.
- Spreading of disease is relatively predictable after certain time, when it stabilizes.
- Given enough time, few diseases would be able to actually infect everyone, but none would be able to kill everyone unless set at extreme values.