Difference between revisions of "Simulace automatizovaneho nakladani kamionu"
(Created page with "__TOC__ == Zadání == '''Název simulace:''' Simulace automatizovaného nakládání kamionů '''Autor:''' Kenan Dervišević '''Typ modelu:''' Multiagentní '''Modelova...") |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 23: | Line 23: | ||
Níže je zobrazeno, jak vypadá rozhraní simulace. | Níže je zobrazeno, jak vypadá rozhraní simulace. | ||
| − | [[File: | + | [[File:7qa1123.png|1000px]] |
== Model == | == Model == | ||
| Line 66: | Line 66: | ||
# <b>truck-arrival</b> - počet přicházejících kamionů každou minutu | # <b>truck-arrival</b> - počet přicházejících kamionů každou minutu | ||
# <b>show-start-time</b> - zobrazení ticku, ve kterém přijel kamion | # <b>show-start-time</b> - zobrazení ticku, ve kterém přijel kamion | ||
| − | # <b> | + | # <b>equation</b> - strategie pochybu jeřábů |
# <b>semi-commited</b> - aktivace penalizace | # <b>semi-commited</b> - aktivace penalizace | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Výsledky == | == Výsledky == | ||
| Line 157: | Line 144: | ||
== Ke stažení == | == Ke stažení == | ||
| − | [[File:nakladani_kamionu.nlogo]] | + | [[File:nakladani_kamionu.nlogo]] simulace v programu NetLogo 5.3.1 |
== Zdroje == | == Zdroje == | ||
Latest revision as of 00:22, 8 June 2018
Contents
Zadání
Název simulace: Simulace automatizovaného nakládání kamionů
Autor: Kenan Dervišević
Typ modelu: Multiagentní
Modelovací nástroj: NetLogo[1]
Definice problému
Kvůli obavám o životní prostředí se provozovatelé automatizovaných nakládacích terminálů na kamiony stále více snaží o zkrácení doby, kdy kamiony stojí. Vysoká cena robotických jeřábů pro převoz kontejnerů jim často zakazuje nakupovat více nástrojů. Dalším důvodem je to, že neexistují jasné studie jak dostupnost a servisní strategie jeřábů ovlivňují čas zatáčení kamionu. Tento model zavádí přístup založený na agentech k modelování jeřábů pro analýzu času zatáčení kamionů. Toho je dosaženo pomocí modelování jeřábů tak, aby měly maximální účinnost. Model se pokusí identifikovat sadu užitečných funkcí, které správně zachycují zásadní rozhodovací proces operátorů jeřábů při výběru dalšího vozíku pro poskytování služeb. Budou použité tři různé metody optimalizace pohybu robotických jeřábů. První bude na základě vzdálenosti určitých kamionů od robotických jeřábu modelovat pohyb a nakládání kontejnerů. Druhá bude dělat to samé, ale na základě délky času čekání a nakládání kontejnerů. Třetí funkce bude kombinací předchozích dvou. Parametry modelu: kamiony (budou přicházet náhodně, podle Poissonova rozdělení), kontejnery, jeřáby
Cíl simulace
Výsledky simulace ukážou, jaká strategie je nejvhodnější a produkuje nejlepší výsledky, pokud jde o průměrnou čekací dobu a maximální čekací dobu kamionu.
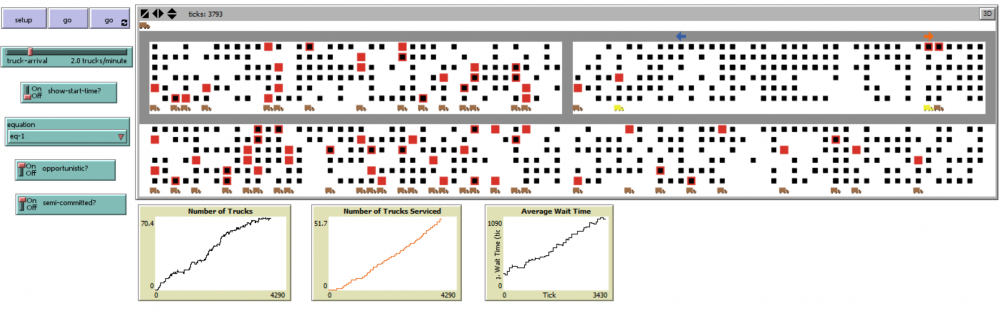
Grafické rozhraní
Níže je zobrazeno, jak vypadá rozhraní simulace.
Model
Parametry modelu:
- Kontejnery
- Jeřáby
- Kamiony (budou přicházet náhodně, podle Poissonova rozdělení)
Model se zabývá případem, kdy je několik jeřábů zodpovědných za obsluhu kamionů, které vybírají kontejnery umístěné ve čtyřech různých blocích. Předpokládáme, že všechny kontejnery mají délku 40 stop (podle normy ISO[2]).
Jeřáby jsou znázorněny šipkami. Pro účely validace jsou zvoleny šipky, protože poskytují směr pohybu jeřábu. Kamiony jsou zobrazeny v hnědé barvě a kontejnery, které je třeba zvednout, jsou zobrazeny červeně. Předpokládá se, že kamiony dorazí podle Poissona rozdělení, s průměrnou rychlostí 10 kamionů za hodinu na blok. Šedé plochy označují trasy cesty jeřábů. Ve skutečnosti existují čtyři bloky. Kontejnery lze na sobě skládat až čtyři. Jeřáby se mohou pohybovat kolem těchto čtyř bloků a mohou se postavit na libovolný blok. Model je implementován tak, aby fungoval pro libovolný počet jeřábů. Kontejnery jsou distribuovány náhodně přes čtyři bloky a nikdy více než čtyři na sobě v jednom řádku. Každému kamionu je přiřazen náhodně vybraný kontejner. Je-li na bloku, kde se kontejner nachází, další kamion, pak kamion čeká v čekárně, dokud není obsloužen jiný kamion, odjede a uvolní další místo.
Každý jeřáb vyhodnotí všechny kamiony a vybere si kamion i, který má největší hodnotu pro obsluhu. Pro účely srovnání jsou vytvořeny tři různé funkce založené na skutečných atributech reálného světa, času a vzdálenosti.
Funkce na základě vzdálenosti:
U(i) = 0 - (vzdálenost od jeřábu) - penalizace x (jiný jeřáb na cestě) - penalizace x (potřeba otočit se?)
- penalizace x (změnit směr?) - penalizace x (není nejbližší jeřáb)
Funkce na základě času čekání:
U(i) = (doba čekání kamionu) - penalizace x (jiný jeřáb na cestě) - penalizace x (potřeba otočit se?)
- penalizace x (změnit směr?) - penalizace x (není nejbližší jeřáb)
Funkce na základě kombinace vzdálenost-čas čekání:
U(i) = (doba čekání kamionu) - (vzdálenost do jeřábu) - penalizace x (jiný jeřáb na cestě)
- penalizace x (potřeba otočit se?) - penalizace x (změnit směr?) - penalizace x (není nejbližší jeřáb)
Penalizace ve výše uvedených funkcích odrazuje jeřáb od volby kamionu, který má další jeřáb v jeho cestě, vyžaduje změnu směru nebo má jiný jeřáb blíž k němu. Kromě těchto pevně stanovených sankcí existuje i variabilní penalizace, pokud se jeřáb rozhodne obsluhovat další kamion s vyšší užitečností obsluhy při cestě k prvotnímu kamionu, který dosud poskytoval nejvyšší hodnotu pro obsluhu. Konečně je pro obsluhu stanoven limit; pod kterým se jeřáb rozhodne zůstat na místě a neslouží žádnému kamionu. Při modelování rychlosti jeřábu a doby manipulace se používají skutečné nebo empirické údaje. Typický jeřáb má rychlost 135 metrů za minutu. Jak již bylo zmíněno dříve, čekací doba kamionu je kombinací doby, kdy jeřáb dorazí do místa, kde je kamion zaparkován, a čas, kdy jeřáb provádí jak přesuny, tak i nakládání. Tyto kroky se opakují pro každý kontejner.
Model implementuje diskrétní simulaci, kde každý “tick” odpovídá jedné sekundě reálného času. Při každém “ticku” model vytvoří a umístí nové kamiony, které by mohly přijet během tohoto “ticku”, požádá jeřáby, aby provedly zvolenou akci pro “tick”, a aktualizuje grafy. Jelikož činnosti jeřábů vyžadují více než jednu sekundu, model zahrnuje časy čekání pro každou akci. Například, jeřáb se po uplynutí šesti sekund pohybuje z jednoho místa na druhé. Namísto toho, aby se jeřáb pokaždé posunul jednu šestinu vzdálenosti, model ho čeká na prvních pět sekund a poté provede posun během šesté sekundy. Tato technika zpoždění se používá pro všechny ostatní akce: přesunutí kontejneru z jednoho řádu do druhého (40 sekund) a přesunutí kontejneru z řady do kamionu (87 sekund).
Implementace má hlavní smyčku, která se vyvolává při každém “ticku”. Nejdříve vytvoříme nové příjezdy kamionu a pak každý jeřáb provede pohyb. Každý jeřáb udržuje cílovou proměnnou, která obsahuje název cíle (goal.name) a počet “ticků”, které jeřáb musí čekat před provedením skutečné akce (goal.ticks). Pouze když je cílová hodnota nulová bude jeřáb provádět kroky směrem k jeho cíli. Pokud je jeřáb připraven k akci a jeho cíl je buď prázdný, nebo má cíl přesunout se do některé určené pozice, nejdříve provede kontrolu, aby se zajistilo, že jeho současný cíl je skutečně nejlepší. Pokud existuje jiný cíl s lepší hodnotou, která je větší od současné aspoň o hodnotu penalizace (0, 100 nebo 10000), pak změní svůj cíl na nový nejlepší. Jeřáb pak provede své kroky, buď se přesune do dalšího bloku nebo přesune kontejner a znovu nastaví svůj cíl.
Vstupní parametry
Průběh simulace je ovlivněn nastavitelnými parametry.
- truck-arrival - počet přicházejících kamionů každou minutu
- show-start-time - zobrazení ticku, ve kterém přijel kamion
- equation - strategie pochybu jeřábů
- semi-commited - aktivace penalizace
Výsledky
Společným ukazatelem výkonnosti je průměrná doba nakládání kamionu. V této simulaci je čas nakládaní kamionu představen jednoduše jako čekací doba, než jeřáb přijede do kamionu, a čas potřebný k tomu, aby jeřáb provedl potřebné kroky vyzvednutí a nakládání kontejneru na kamion. Průměrné čekací doby kamionů jsou uvedeny ve druhém sloupci tabulky 1, pro dva jeřáby. Tyto doby čekání jsou zprůměrovány na 10 simulačních běhů. V tabulce 1 je vidět, že funkce založená na vzdálenosti poskytuje nejnižší průměrný čas čekání u všech tří případů. Když je penalizace nulová, jeřáby by se měly chovat oportunisticky. To znamená, že by jeřáby vyhodnotily užitečnost všech kamionů a následně, v každém kroku, obsluhovaly ten s nejvyšší užitečnosti. Naopak, penalizace 10000 znamená, že jeřáby by neměly být oportunistické a neměly by obsluhovat jiné kamiony, dokud nedokončí službu pro své plánované kamiony (které předtím měly nejvyšší užitečnost). Vidíme, že průměrná doba čekání pro funkce založenou na vzdálenosti je nejnižší, když je penalizace nastavena na hodnotu 0.
| Typ | Penalizace | Průměrná doba čekání (min) | Maximální doba čekání (min) |
|---|---|---|---|
| Funkce na základě vzdálenosti | |||
| 0 | 14.37 | 41.30 | |
| 100 | 15.42 | 37.93 | |
| 10000 | 15.04 | 45.65 | |
| Funkce na základě času čekání | |||
| 0 | 68.97 | 68.95 | |
| 100 | 65.49 | 72.58 | |
| 10000 | 53.84 | 56.18 | |
| Funkce na základě kombinace vzdálenost-čas čekání | |||
| 0 | 68.04 | 86.38 | |
| 100 | 65.42 | 67.97 | |
| 10000 | 52.24 | 56.77 |
Průměrná čekací doba, když jeřáby postupují podle funkce založené na čase, v porovnání s s funkci založené na vzdálenosti, je téměř čtyřikrát vyšší. Podobně, funkce založená na čase a vzdálenosti nebyla lepší. Důvod pro to je zřejmý při prohlížení simulace. Když jeřáby pracovaly na minimalizaci čekací doby kamionů, měly dlouhé jízdy od jednoho konce střediska k druhému, přičemž ignorovali kamiony, které byly blíž. Bylo by mnohem efektivnější, kdyby využili čas, aby sloužili blízkým kamionům.
| Typ | Penalizace | Průměrná doba čekání (min) | Maximální doba čekání (min) |
|---|---|---|---|
| Funkce na základě vzdálenosti | |||
| 0 | 6.53 | 19.05 | |
| 100 | 6.82 | 20.78 | |
| 10000 | 6.77 | 19.90 | |
| Funkce na základě času čekání | |||
| 0 | 8.75 | 21.95 | |
| 100 | 8.51 | 24.47 | |
| 10000 | 7.85 | 21.27 | |
| Funkce na základě kombinace vzdálenost-čas čekání | |||
| 0 | 7.85 | 21.07 | |
| 100 | 7.88 | 22.37 | |
| 10000 | 8.11 | 19.58 |
Tabulka 2 zobrazuje dobu čekání, pokud jsou k dispozici tři jeřáby. Je vidět výrazný pokles průměrné doby čekání a minimální doby čekání ve všech třech typech funkcí. Je také zajímavé poznamenat, že se třemi jeřáby je výkonnost časové funkce a funkce založené na kombinaci čas-vzdálenost blíž výsledku funkce založené na vzdálenosti. Důvodem je menší vzdálenost, kterou musí “pokrývat” jeden jeřáb.
Závěr
Tato simulace zavedla přístup modelování jeřábů tak, aby měly maximální účinnost při nakládání kamionů. Byla identifikována sada užitečných funkcí, které správně zachytily základní rozhodovací kritéria provozovatelů jeřábu při výběru dalšího vozíku, kterému má poskytovat služby. Výsledky simulace ukázaly, že jestliže jeřáby vyberou kamiony, které jsou nejblíže k nim, aniž by bylo nutné jeřáby často otáčet (časově náročný proces) a obrátit směr, pak celkový výkon systému, pokud jde o průměrnou dobu čekání a maximální čekací dobu kamionu bude lepší, než kdyby si vybraly kamiony na základě jejich čekací doby. Pomocí funkcí můžeme jasně a explicitně zachytit, jak jeřáby vyvažují různé priority jako je například vzdálenost ke kamionům a čas čekání na kamiony.
Ke stažení
File:Nakladani kamionu.nlogo simulace v programu NetLogo 5.3.1
Zdroje
- ↑ Wilensky, U. (1999). NetLogo. http://ccl.northwestern.edu/netlogo/. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.
- ↑ Shipping Containers for Storage https://www.mrbox.co.uk/shipping-containers/