Difference between revisions of "Queueing theory/cs"
(→Vzorce) |
(→základní informace nutné k výpočtu) |
||
| Line 11: | Line 11: | ||
* Systém realizující obsluhu | * Systém realizující obsluhu | ||
* Časová posloupnost výstupu | * Časová posloupnost výstupu | ||
| − | === | + | ===Základní informace nutné k výpočtu=== |
| + | Pro návrh systémů hromadné obsluhy je nutné znát základní parametry: | ||
* Vstupní tok | * Vstupní tok | ||
| − | zákazníci mohou do systému vstupovat jednotlivě nebo hromadně | + | "zákazníci" mohou do systému vstupovat jednotlivě nebo hromadně |
* Frontový režim | * Frontový režim | ||
| − | FIFO (First-in-First-out), LIFO (Last-in-First-out), SIRO (Service in Random Order), PRI (Priority queue) | + | systém, jakým jsou zákazníci čekající na obsluhu řazeni do systému - FIFO (First-in-First-out), LIFO (Last-in-First-out), SIRO (Service in Random Order), PRI (Priority queue) |
* Organizace obsluhy | * Organizace obsluhy | ||
| − | zda je k dispozici jeden obslužný systém, paralelní zapojení systémů | + | zda je k dispozici jeden obslužný systém, paralelní či sériové zapojení systémů |
[[File:Xblal26_SHO.jpg]] | [[File:Xblal26_SHO.jpg]] | ||
Revision as of 13:45, 15 June 2015
Contents
Teorie hromadné obsluhy (Teorie front)
Jednou z podskupin diskrétních simulací je teorie hromadné obsluhy, v češtině často nazývaná jako "Teorie front".
Úvod
Teorie front zkoumá systémy, na které opakovaně přicházejí sekvence požadavků a jejich výskyt je náhodný. Zjišťujeme tak například potřebnou kapacitu zdrojů, nebo optimální využití výrobních linek. Tato chování se dají nasimulovat do tzv. stochastických modelů. Cílem těchto modelů je analýza stávajících systémů a nalezení nejvhodnějšího způsobu optimalizace. Zároveň se musí optimalizovat množství lidí čekajících ve frontě a vytížení obslužných linek. Pro simulování frontových systémů potřebujeme informace o vstupním toku (např. jak často přijde nový požadavek na server), o frontovém systému, který se vytvoří, pokud požadavek nemůže být ihned vyřízen a organizace obsluhy - počet volných jednotek vykonávající proces obsluhy a jejich popis. Pokud mluvíme o vstupu jako o zákazníkovi, nejedná se o zákazníka v striktním slova smyslu, ale může to být proces, služba, člověk ale i jakýkoliv požadavek čekající na vyřízení.
Schéma teorie front
- Objekty vyžadující obsluhu (zákazníci, jednotky, požadavky)
- Množina jednotek přicházející v úvahu pro hromadnou obsluhu
- Časová posloupnost vstupu jednotek
- Množina jednotek čekajících na obsluhu
- Systém realizující obsluhu
- Časová posloupnost výstupu
Základní informace nutné k výpočtu
Pro návrh systémů hromadné obsluhy je nutné znát základní parametry:
- Vstupní tok
"zákazníci" mohou do systému vstupovat jednotlivě nebo hromadně
- Frontový režim
systém, jakým jsou zákazníci čekající na obsluhu řazeni do systému - FIFO (First-in-First-out), LIFO (Last-in-First-out), SIRO (Service in Random Order), PRI (Priority queue)
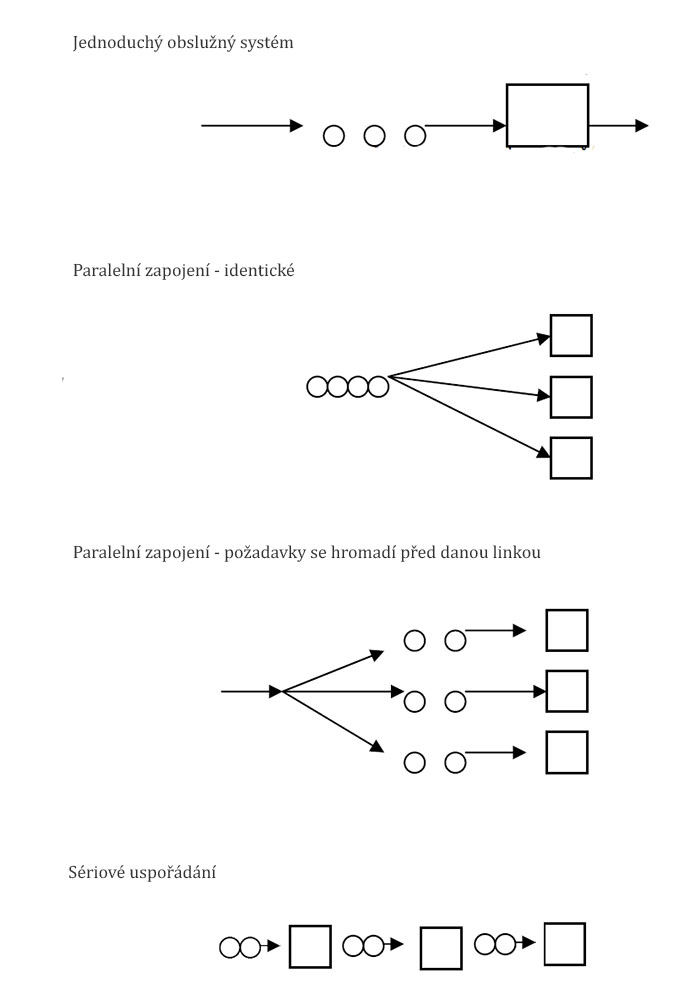
- Organizace obsluhy
zda je k dispozici jeden obslužný systém, paralelní či sériové zapojení systémů
Kendallova klasifikace
D.G. Kendall byl anglický statistik a matematik, v 50. letech zavedl notaci pro jednotnou charakteristiku systémů hromadné obsluhy. Jelikož jsou systémy hromadné obsluhy velmi komplexní, je nutné standardizovat jejich značení pro zjednodušení následných výpočtů.
Jelikož tyto informace nejsou v praxi dostačující, rozšířil se model o další 3 klasifikační třídy.
Na jednotlivé pozice se do modelu dosazují kódy (výsledný model může mít až šestimístný kód - A/B/C/D/E/F)
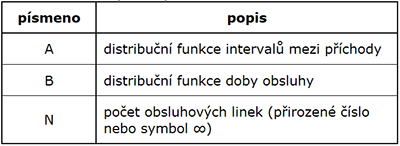
- A
Pravděpodobností rozdělení intervalů mezi příchody požadavků, nejčastěji: N - normální rozdělení M - exponenciální rozdělení U - rovnoměrné rozdělení G - obecné rozdělení
- B
pravděpodobnostní rozdělení doby obsluhy, stejné jako A
- C
počet paralelně zapojených obslužných linek
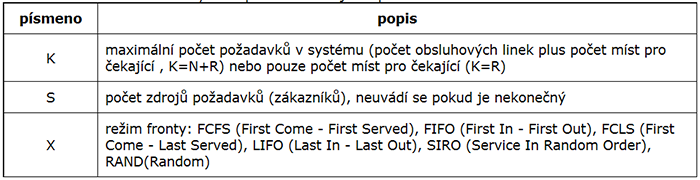
- D
kapacita obslužného systému (neuvedeno = nekonečno)
- E
zdroje požadavků (neuvedeno = nekonečno)
- F
systém fronty (FIFO, LIFO, ...)
např. zápis systému M/M/1/ Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \infty} / Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \infty} /FIFO se zjednodušeně zapíše M/M/1
Vzorce
Pro jednoobslužný systém
* požadavky přichází s Poissonovým rozdělením
* počet požadavků přicházející do systému v intervalu <0;T>, p(n) = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle $\frac{(\lambda T)^n}{n!}$ $e^{({-}\lambda T)}$}