Difference between revisions of "Hearthstone Mulligan"
(→Results) |
(→Model) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 42: | Line 42: | ||
=Model= | =Model= | ||
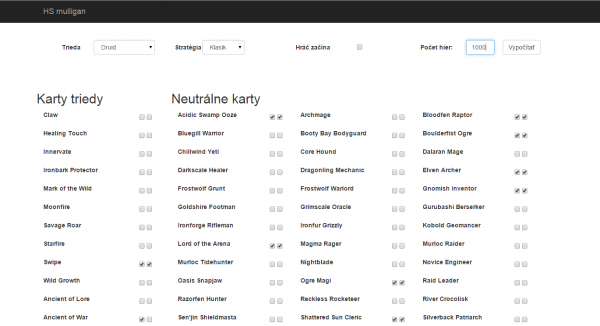
Model is available at [http://startfirmy.sk/hearthstone/ link]. Deck can be selected in form together with other parameters. After submitting the form, scores are calculated. Formula for calculation of score can be found in source code, as functions vypocitaj_score_klasik() and vypocitaj_score_rush() - for classic game and for rush game respectively. Results are displayed and possibility to download .csv file is presented. This file contains draws for all games, as well as scores, and can be used in further analysis. | Model is available at [http://startfirmy.sk/hearthstone/ link]. Deck can be selected in form together with other parameters. After submitting the form, scores are calculated. Formula for calculation of score can be found in source code, as functions vypocitaj_score_klasik() and vypocitaj_score_rush() - for classic game and for rush game respectively. Results are displayed and possibility to download .csv file is presented. This file contains draws for all games, as well as scores, and can be used in further analysis. | ||
| + | |||
| + | [[File:hs1.png|600px]] | ||
=Results= | =Results= | ||
| Line 67: | Line 69: | ||
=Conclusion= | =Conclusion= | ||
| + | Hearthstone is very complex game. Players need to take into account many factors - current meta game, strengths and weaknesses of players' class as well as opponents class, their strategies and anticipate opponents strategies and intentions. This would be practically impossible to simulate. However luck, randomness and statistics play a big role in this game and that's why simulation and simulators are relevant. Although this simulation does not cover all possible situations, it provides useful insight into topic and environment that can be used while creating more complex simulations and analysis. | ||
=Code= | =Code= | ||
| + | [[File:xpalj24_simulation_mulligan.rar]] | ||
=Links= | =Links= | ||
Latest revision as of 02:22, 26 January 2015
- Project name: Hearthstone Mulligan
- Class: 4IT495 Simulation of Systems (WS 2014/2015)
- Author: Juraj Paluch
- Model type: Monte-Carlo Simulation
- Software used: PHP, Javascript, HTML, Microsoft Excel
Contents
Introduction
Hearthstone: Heroes of Warcraft is a free-to-play digital collectible card game that revolves around turn-based matches between two opponents. Players start the game with a substantial collection of 'basic' cards, but can gain rarer and more powerful cards through purchasing packs of cards, or as reward for competing in the Arena. Players can also disenchant unwanted cards, destroying them in exchange for arcane dust, a resource which can be used to create new cards. Card packs and entry to the Arena can be purchased with gold, an in-game currency rewarded for completing randomized daily quests and winning matches, or by using real money in the in-game store.
Each Hearthstone battle is a 1vs1 match between two opponents. Gameplay in Hearthstone is turn-based, with players taking turns to play cards from their hand, casting spells, equipping weapons, or summoning 'minions' to do battle on their behalf. Play may be between two human players, or one player and a computer-controlled opponent.
Each player is represented by their chosen 'hero', an important character from Warcraft lore. Each hero represents a particular class, determining the special cards and unique hero power available to them. Each hero has 30 Health - if that number is reduced to zero, the hero is destroyed, and the controlling player has lost the game. The available classes are Mage, Priest, Warlock, Paladin, Warrior, Druid, Hunter, Rogue and Shaman.
At the start of each turn, the player draws a new card from their deck - a collection of 30 cards selected before starting a game. Players can choose to play using one of several pre-assembled 'basic' decks or a deck of their own making. While most cards are available to heroes of any class, a substantial portion are limited to a specific class, giving each hero their own strengths and unique possibilities.
During their turn, each player can choose to play any of their cards, use their hero power, command their minions to attack targets, or attack directly using their hero, if they have a weapon equipped. However, which actions the player is able to take is partly determined by their mana, a resource pool which is refreshed at the start of each turn. Each player starts the game with 0 mana crystals, and gains one at the start of each turn up to a maximum of 10. Each card and hero power requires the player to expend a specific amount of mana in order to play it, strategically limiting each player's actions. In addition, the larger mana pools in later rounds allow players to play increasingly expensive cards, opening the game up to more powerful minions and abilities.
A match is concluded when one or both players has reached zero health, or chooses to concede.
Goal of this simulation is to simulate early stage of game called "Mulligan".
Problem definition
The match begins with a coin toss to determine who goes first, followed by both players drawing their starting hands: three cards for the coin toss winner, four for the other player. Player can mulligan (drop cards and get new cards from their deck) as many cards from his/her starting hands as he/she likes. Once both players accept their hand, the match begins. Mulligan is very important part of game as players decide what starting hand will they have. Its important to get cards with mana costs that can be played each turn, especially in early rounds - failure to play a card in first rounds often results in great disadvantage or straight loss.
Goal of this simulation thus will be to simulate this stage of game and to help player make a decision on how many cards should be kept during mulligan. First rounds will be simulated as well, to determine success of mulligan.
Method
Simulation is created as web application. Relevant data for Hearthstone cards can be obtained on internet in JSON format. This data was processed with PHP and Javascript and form where input data will be defined was created.
Parameters
Class: players class (certain cards are available only to certain classes)
Strategy: player's preferred strategy
Classic - player prefers cards "on curve", meaning maximizing usage of mana. Generally speaking cards with bigger value are better.
Rush - player wants to win game early, so he/she prefers smaller value cards that can be played early. This way it's possible to play more cards earlier.
Player starts: first player gets fewer cards
Number of games: number of simulations that simulation should run. The more, the better.
Cards: class specific and general cards can be selected
Simulation
After parameters are set, simulation can begin. Selected deck is transformed into associative array and randomly shuffled. First cards are then "drawn". Simulation then uses four (five when player goes second) strategies - keep all cards, drop 1 card or drop multiple cards. Dropped cards are afterwards replaced by other cards selected from deck. After this turn starts - player draws another card. If player has a card that can be played on a certain turn, he/she plays it. Players prefer cards with larger value. Maximum score (points) for turn is 1 - meaning player has a card to play on turn for full mana. If cards with lesser value have to be played, score is lower. 4 turns are played, and total score is calculated for each possibility. With rush strategy, player doesn't get penalized for not playing card with relevant value, but for not being to play as many cards on each turn as possible. In the end, average is calculated for each possibility and most succesful strategy can be decided.
Model
Model is available at link. Deck can be selected in form together with other parameters. After submitting the form, scores are calculated. Formula for calculation of score can be found in source code, as functions vypocitaj_score_klasik() and vypocitaj_score_rush() - for classic game and for rush game respectively. Results are displayed and possibility to download .csv file is presented. This file contains draws for all games, as well as scores, and can be used in further analysis.
Results
Results vary significantly according to selected deck and parameters. For rush decks lower number of dropped cards is needed. For decks focused on longer games, higher card dropping is preferred. For starting player one card dropping is usually recommended, for other player two cards have best results. Interesting result seems to be dropping all cards - usually yields large scores. For one of authors decks results are as follows (player goes second):
| Strategy | Score |
|---|---|
| Keep all cards | 2.86529 |
| Drop 1 card | 2.88521 |
| Drop 2 cards | 3.11954 |
| Drop 3 cards | 2.93745 |
| Drop 4 cards | 3.00585 |
Conclusion
Hearthstone is very complex game. Players need to take into account many factors - current meta game, strengths and weaknesses of players' class as well as opponents class, their strategies and anticipate opponents strategies and intentions. This would be practically impossible to simulate. However luck, randomness and statistics play a big role in this game and that's why simulation and simulators are relevant. Although this simulation does not cover all possible situations, it provides useful insight into topic and environment that can be used while creating more complex simulations and analysis.
Code
File:Xpalj24 simulation mulligan.rar