Difference between revisions of "Multistage Games/cs"
| Line 39: | Line 39: | ||
Pokud se ve hře ''1,2, ..., t−1'' stane to a to, pak ve hře ''t'' zvolím akci ''a''. | Pokud se ve hře ''1,2, ..., t−1'' stane to a to, pak ve hře ''t'' zvolím akci ''a''. | ||
| − | Pokud se podíváme znovu na první hru, tak tato hra má čtyři možné výsledky. Každý hráč by měl mít naplánovanou strategii pro další hru pro každý z těchto výsledků. | + | [[File:Two-stage-game.png|150px|thumb|right]] |
| + | |||
| + | |||
| + | |||
| + | |||
| + | Pokud se podíváme znovu na první hru, tak tato hra má čtyři možné výsledky. Každý hráč by měl mít naplánovanou strategii pro další hru pro každý z těchto výsledků, protože nikdy neví, jak bude hrát protihráč. Všechny možné situace je dobré znázornit např. pomocí stromového grafu. | ||
| + | |||
| + | |||
| + | |||
== Zdroje == | == Zdroje == | ||
<references/> | <references/> | ||
Revision as of 22:14, 17 June 2014
Contents
Úvod
Pojmem vícekolové hry rozumíme situaci, kdy stejní hráči hrají postupně Jednorázové hry, kde reagují na výsledek hry předchozí. Hráči dle výsledku předchozích her rozhodují o svých následujících tazích.
Vícekolové hry patří mezi hry v rozšířené formě, kdy hráči rozhodují konfliktní situaci po tazích. Rozhodnutí jednoho hráče o volbě jeho strategie ovlivňují předchozí tahy ostatních hráčů. Celá hra je procesem sekvence rozhodnutí jednotlivých hráčů.[1]
Definice
(1) V každém kole Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k} znají všichni hráči všechny tahy, provedené v předchozích kolech, (2) každý hráč má v každém z kol nanejvýš jeden tah a (3) žádná z informačních sad pro právě hrané kolo nepopisuje plánované tahy jednotlivých hráčů.
Vícekolová hra je konečná posloupnost jednorázových her, kde každá z nich je hra s úplnou ale nedokonalou informací. Tyto hry jsou hrány postupně stejnými hráči a celkový zisk je určen dle výsledků jednotlivých her. Je zde předpoklad, že každá hra je hrána v odlišnou dobu, tedy že hra č.1 je hrána v době č.1, hra č.2 v době č.2, atd. Předpokladem také je, že výsledek každé hry je znám všem hráčům.[2]
Je důležité si uvědomit, že hráči, když vědí, že bude následovat další hra, mohou plánovat a podmínit si své tahy v budoucích hrát na základě výsledků aktuální hry či na základě výsledků již proběhlých her.
Ukázka hry
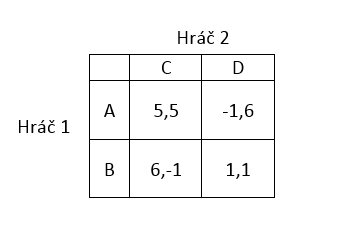
Mějme dva hráče, kteří hrají hru typu vězňovo dilema. Každý z hráčů tedy může buď mluvit a přiznat se (B,D), nebo zapírat a spoléhat na to, že druhý hráč udělá to samé (A,C).
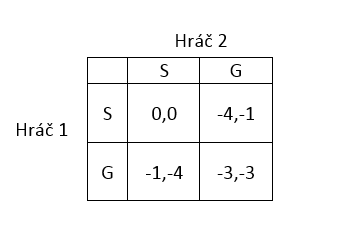
Po dohrání této hry (a odpykání si patřičných let) se oba hráči dostávají do možnosti odplaty a ocitnout v situaci, kdy každý z nich se může přidat do gangu (G) nebo zůstat sám (S). Situace je znázorněna v následující matici.
Pokud oba hráči zvolí S, tak bez ohledu na výsledek předešlé hry si každý půjde svou cestou, a zisk obou je 0. Pokud oba vstoupí do gangu (G), budou spolu bojovat, utrží ztrátu a jejich výsledný zisk bude -3. Třetí situace je, když jeden z hráčů zvolí vstup do gangu (G) a druhý zůstane sám (S). Ten co bude sám se neubrání a utrpí velkou ztrátu -4. Druhý hráč, který se stal součástí gangu, je pouze mírně zraněn, a jeho zisk z této hry je -1.
Pokud budeme každou z výše uvedených her hrát samostatně, hráči nebudou hry brát v souvislostech a budou se snažit v každé dosáhnout nejlepšího výsledku. Pokud ale hráč ví, že hry budou na sebe navazovat, má možnost vytvořit si strategii a chovat se podle toho.
Vezměme si hráče 1. Hráč 1 se rozhodne, že v 1. hře bude hrát B (mluvit) a ve 2. hře bude hrát S (sám) pouze v tom případě, pokud hráč 2 bude v první hře hrát C (zapírat). V tomto případě by hráč 1 měl z první hry zisk 6 a z druhé hry 0.
Pokud ale hráč 2 v první hře bude mluvit (D), hráč 1 má naplánováno, že v druhé hře bude hrát G (gang).
Tuto strategii lze obecně zapsat takto:
Pokud se ve hře 1,2, ..., t−1 stane to a to, pak ve hře t zvolím akci a.
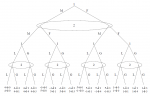
Pokud se podíváme znovu na první hru, tak tato hra má čtyři možné výsledky. Každý hráč by měl mít naplánovanou strategii pro další hru pro každý z těchto výsledků, protože nikdy neví, jak bude hrát protihráč. Všechny možné situace je dobré znázornit např. pomocí stromového grafu.
Zdroje
- ↑ DLOUHÝ, Martin; FIALA, Petr. Úvod do teorie her. 2.přepracované vydání. Vysoká škola ekonomická v Praze : Nakladatelství Oeconomica, 2009. 120 s. ISBN 978-80-245-1609-7.
- ↑ Tadelis, Steve. Game Theory: An Introduction. Princeton: Princeton UP, 2013. Print. http://faculty.haas.berkeley.edu/stadelis/Game%20Theory/econ160_week5.pdf