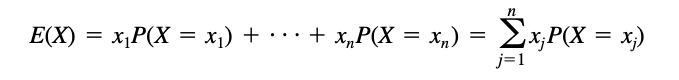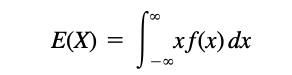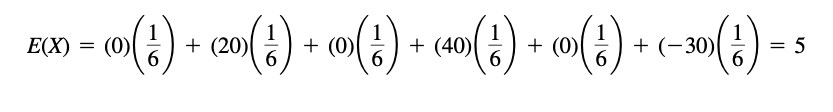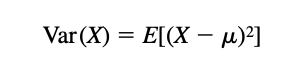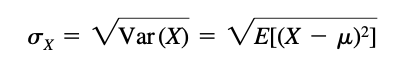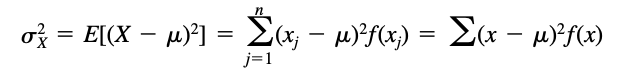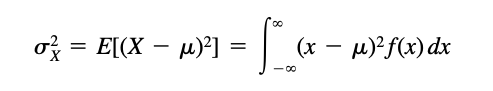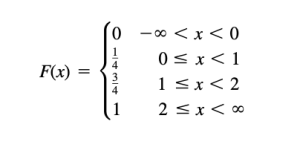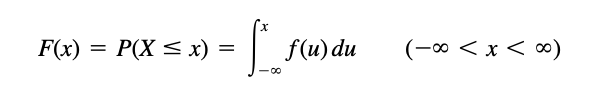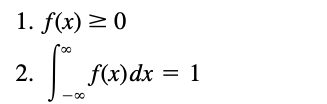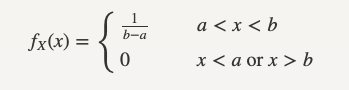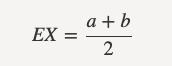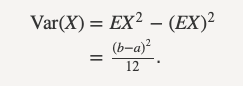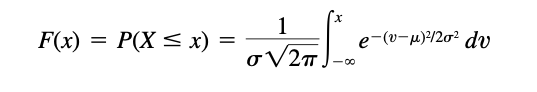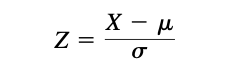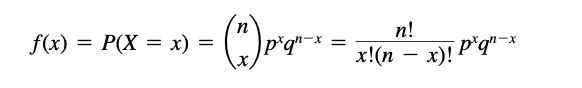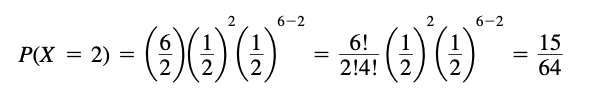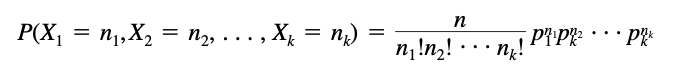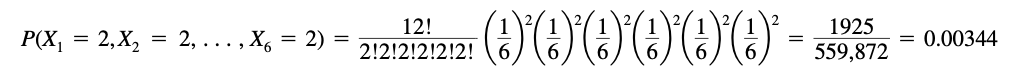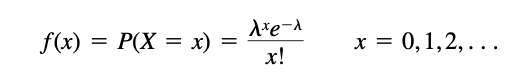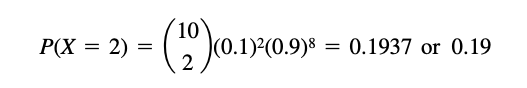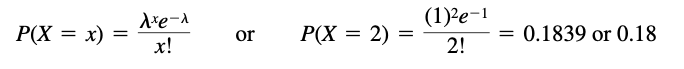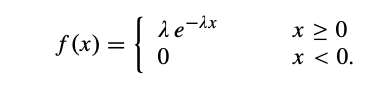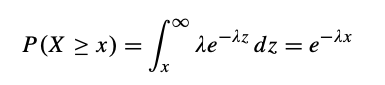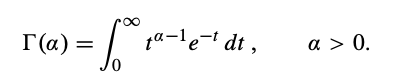Difference between revisions of "Probability distributions"

From Simulace.info
Jump to: navigation, search
 
(196 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
In [[probability theory]] and [[statistics]], a '''probability distribution''' is the mathematical [[Function (mathematics)|function]] that gives the probabilities of occurrence of different possible '''outcomes''' for an [[Experiment (probability theory)|experiment]].<ref name=":02">{{Cite book|title=The Cambridge dictionary of statistics|last=Everitt | first = Brian |date=2006|publisher=Cambridge University Press|isbn=978-0-511-24688-3 |edition=3rd|location=Cambridge, UK|oclc=161828328}}</ref><ref>{{Cite book|title=Basic probability theory|last=Ash, Robert B.|date=2008|publisher=Dover Publications |isbn=978-0-486-46628-6 |edition=Dover |location=Mineola, N.Y. |pages=66–69|oclc=190785258}}</ref> It is a mathematical description of a [[Randomness|random]] phenomenon in terms of its [[sample space]] and the [[Probability|probabilities]] of [[Event (probability theory)|events]] ([[subset]]s of the sample space).<ref name=":1">{{cite book|title=Probability and statistics: the science of uncertainty|last1=Evans |first1=Michael |date=2010|publisher=W.H. Freeman and Co|last2=Rosenthal |first2=Jeffrey S. |isbn=978-1-4292-2462-8 |edition=2nd|location=New York|pages=38|oclc=473463742}}</ref>
+
In probability theory and statistics, a '''probability distribution''' is the mathematical function that gives the probabilities of occurrence of different possible '''outcomes''' for an experiment. In any random experiment there is always uncertainty as to whether a particular event will or will not occur. As a measure of the chance, or probability, with which we can expect the event to occur, it is convenient to assign a number between 0 and 1. <ref name="probz">Spiegel, M. R., Schiller, J. T., & Srinivasan, A. <i>Probability and Statistics : based on Schaum’s outline of Probability and Statistics</i>, published 2001 https://ci.nii.ac.jp/ncid/BA77714681</ref>
  
−
For instance, if {{mvar|X}} is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of {{mvar|X}} would take the value 0.5 (1 in 2 or 1/2) for {{math|1=''X'' = heads}}, and 0.5 for {{math|1=''X'' = tails}} (assuming that [[fair coin|the coin is fair]]). Examples of random phenomena include the weather conditions at some future date, the height of a randomly selected person, the fraction of male students in a school, the results of a [[Survey methodology|survey]] to be conducted, etc.<ref name="ross" />
 
  
 
==Introduction==
 
==Introduction==
−
[[File:Dice Distribution (bar).svg|thumb|250px|right|The [[probability mass function]] (pmf) <math>p(S)</math> specifies the probability distribution for the sum <math>S</math> of counts from two [[dice]]. For example, the figure shows that <math>p(11) = 2/36 = 1/18</math>. The pmf allows the computation of probabilities of events such as <math>P(X > 9) = 1/12 + 1/18 + 1/36 = 1/6</math>, and all other probabilities in the distribution.]]
+
Probability is the science of uncertainty. It provides precise mathematical rules for understanding and analyzing our own ignorance. It does not tell us tomorrow’s weather or next week’s stock prices; rather, it gives us a framework for working with our limited knowledge and for making sensible decisions based on what we do and do not know.<ref name="probzz"> Evans, M. J., & Rosenthal, J. S.<i>Probability and Statistics: The Science of Uncertainty</i>, published 2009, WH Freeman. </ref>
  
−
A probability distribution is a mathematical description of the probabilities of events, subsets of the [[sample space]]. The sample space, often denoted by <math>\Omega</math>, is the [[Set (mathematics)|set]] of all possible [[Outcome (probability)|outcomes]] of a random phenomenon being observed; it may be any set: a set of [[real numbers]], a set of [[vector (mathematics)|vectors]], a set of arbitrary non-numerical values, etc. For example, the sample space of a coin flip would be {{math|1=Ω = {heads, tails}<nowiki/>}}.
+
== Terminology ==
 +
=== Sample space  ===
 +
In probability theory, the sample space refers to the set of all possible outcomes of a random experiment. It is denoted by the symbol Ω (capital omega).<ref name="probiiiz"> Casella, G., & Berger, R. L. <i> Statistical Inference. </i>, published 2021, Cengage Learning. </ref>
 +
 
 +
* Let's consider an example of rolling a fair six-sided die. The sample space in this case would be {1, 2, 3, 4, 5, 6}, as these are the possible outcomes of the experiment. Each number represents the face of the die that may appear when it is rolled. <ref name="probiiiz"> Casella, G., & Berger, R. L. <i> Statistical Inference. </i>, published 2021, Cengage Learning. </ref>
 +
 
 +
=== Random variable ===
 +
Random variable takes values from a sample space. In contrast, probabilities describe which values and set of values are more likely to be taken out of the sample space. Random variable must be quantified, therefore, it assigns a numerical value to each possible outcome in the sample space. <ref name="probzz"> Evans, M. J., & Rosenthal, J. S.<i>Probability and Statistics: The Science of Uncertainty</i>, published 2009, WH Freeman. </ref>
 +
 
 +
* For example, if the sample space for flipping a coin is {heads, tails}, then we can assign a random variable Y such that Y = 1 when heads land and Y = 0 when tails land. However, we can assign any number for these variables. 0 and 1 are just more convenient.  <ref name="probzz"> Evans, M. J., & Rosenthal, J. S.<i>Probability and Statistics: The Science of Uncertainty</i>, published 2009, WH Freeman. </ref>
 +
 
 +
* Because random variables are defined to be functions of the outcome s, and because the outcome s is assumed to be random (i.e., to take on different values with different probabilities), it follows that the value of a random variable will itself be random (as the name implies).
 +
 
 +
Specifically, if X is a random variable, then what is the probability that X will equal some particular value x? Well, X = x precisely when the outcome s is chosen such that X(s) = x.
 +
 
 +
* '''Exercise'''
 +
** Suppose that a coin is tossed twice so that the sample space is S = {HH, HT, TH, TT}. Let X represent the '''number of heads''' that can come up. With each sample point we can associate a number for X as shown in Table 1. Thus, for example, in the case of HH (i.e., 2 heads), X = 2 while for TH (1 head), X 􏰂= 1. It follows that X is a random variable. <ref name="probzz"> Evans, M. J., & Rosenthal, J. S.<i>Probability and Statistics: The Science of Uncertainty</i>, published 2009, WH Freeman. </ref>
 +
 
 +
[[File:Tablespace.png|center|[[Probability distributions#Sample Space - sample|Table 1. Sample Space]]]]
 +
 
 +
=== Expected value ===
 +
A very important concept in probability is that of the '''expected value''' of a random variable. For a discrete random variable ''X'' having the possible values ''x1, c, xn,'' the expectation of ''X'' is defined as: <ref name="probzz"> Evans, M. J., & Rosenthal, J. S.<i>Probability and Statistics: The Science of Uncertainty</i>, published 2009, WH Freeman. </ref>
 +
 
 +
[[File:ex.png|center|]]
 +
 
 +
For a continuous random variable ''X'' having density function ''f(x)'', the expectation of ''X'' is defined as
 +
[[File:excont.png|center|]]
 +
 
 +
==== Example ====
 +
Suppose that a game is to be played with a single die assumed fair. In this game a player wins $20 if a 2 turns up, $40 if a 4 turns up; loses $30 if a 6 turns up; while the player neither wins nor loses if any other face turns up. Find the expected sum of money to be won.
 +
 
 +
[[File:exex.png|center|]]
 +
 
 +
=== Variance and standard deviation ===
 +
Another important quantity in probability is called the '''variance''' defined by:
 +
[[File:var.png|center|]]
 +
The variance is a nonnegative number. The positive square root of the variance is called the '''standard deviation'''
 +
and is given by
 +
[[File:standdev.png|center|]]
 +
 
 +
*If ''X'' is a '''discrete''' random variable taking the values ''x1, x2, . . . , xn'' and having probability function ''f(x)'', then the variance is given by
 +
[[File:vardisc.png|center|]]
 +
 
 +
*If ''X'' is a '''continuous''' random variable having density function ''f(x)'', then the variance is given by
 +
[[File:varcont.png|center|]]
 +
 
 +
*'''Graphical representation''' of variance for 2 continuous distribution with the same mean ''μ'' can be seen in a graph bellow
 +
[[File:vargraph.png|center|]]
 +
 
 +
== PMF vs. PDF vs. CDF  ==
 +
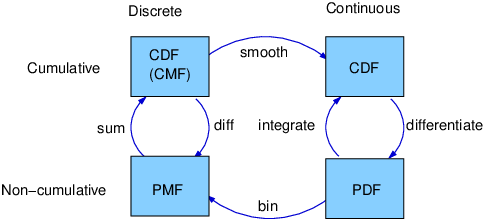
In probability theory there are 3 functions that might be little confusing for some people. Let's make the differences clear.
 +
[[File:pdf.png|center]]  
 +
 
 +
==== Probability mass function (PMF)  ====
 +
*The probability mass function, denoted as ''P(X = x)'', is used for discrete random variables. It assigns probabilities to each possible value that the random variable can take. The PMF gives the probability that the random variable equals a specific value.
 +
 
 +
==== Cumulative distribution function (CDF) ====
 +
* The cumulative distribution function, denoted as ''F(x)'', describes the probability that a random variable takes on a value less than or equal to a given value ''x''. It gives the cumulative probability up to a specific point.
 +
* Since the PDF is the derivative of the CDF, '''the CDF can be obtained from PDF by integration'''
 +
 
 +
==== Probability density function (PDF) ====
 +
To determine the distribution of a '''discrete''' random variable we can either provide its '''PMF''' or '''CDF'''. For '''continuous''' random variables, the CDF is well-defined so we can provide the '''CDF'''. However, the PMF does '''not''' work for continuous random variables, because for a continuous random variable ''P(X=x)=0'' for all x ∈ ℝ.
 +
*Instead, we can usually define the probability density function (PDF). The '''PDF''' is the density of probability rather than the probability mass. The concept is very similar to mass density in physics: its unit is probability per unit length. <ref name="probz">Spiegel, M. R., Schiller, J. T., & Srinivasan, A. <i>Probability and Statistics : based on Schaum’s outline of Probability and Statistics</i>, published 2001 https://ci.nii.ac.jp/ncid/BA77714681</ref>
 +
 
 +
* The probability density function (PDF) is a function used to describe the probability distribution of a continuous random variable. Unlike discrete random variables, which have a countable set of possible values, continuous random variables can take on any value within a specified range. <ref name="probz">Spiegel, M. R., Schiller, J. T., & Srinivasan, A. <i>Probability and Statistics : based on Schaum’s outline of Probability and Statistics</i>, published 2001 https://ci.nii.ac.jp/ncid/BA77714681</ref>
  
−
To define probability distributions for the specific case of [[random variables]] (so the sample space can be seen as a numeric set), it is common to distinguish between '''discrete''' and '''absolutely continuous''' [[random variable]]s. In the discrete case, it is sufficient to specify a [[probability mass function]] <math>p</math> assigning a probability to each possible outcome: for example, when throwing a fair [[dice]], each of the six values 1 to 6 has the probability 1/6. The probability of an [[Event (probability theory)|event]] is then defined to be the sum of the probabilities of the outcomes that satisfy the event; for example, the probability of the event "the die rolls an even value" is
+
* The PDF, denoted as ''f(x)'', represents the density of the probability distribution of a continuous random variable at a given point ''x''. It provides information about the likelihood of the random variable taking on a specific value or falling within a specific range of values.
−
<math display="block">p(2) + p(4) + p(6) = 1/6 + 1/6 + 1/6 = 1/2.</math>
+
* Since the '''PDF is the derivative of the CDF''', the CDF can be obtained from PDF by integration <ref name="probz">Spiegel, M. R., Schiller, J. T., & Srinivasan, A. <i>Probability and Statistics : based on Schaum’s outline of Probability and Statistics</i>, published 2001 https://ci.nii.ac.jp/ncid/BA77714681</ref>
  
−
In contrast, when a random variable takes values from a continuum then typically, any individual outcome has probability zero and only events that include infinitely many outcomes, such as intervals, can have positive probability. For example, consider measuring the weight of a piece of ham in the supermarket, and assume the scale has many digits of precision. The probability that it weighs ''exactly'' 500&nbsp;g is zero, as it will most likely have some non-zero decimal digits. Nevertheless, one might demand, in quality control, that a package of "500&nbsp;g" of ham must weigh between 490&nbsp;g and 510&nbsp;g with at least 98% probability, and this demand is less sensitive to the accuracy of measurement instruments.
+
[[File:statszz.png|center|]]
  
−
[[File:Combined Cumulative Distribution Graphs.png|thumb|455x455px|The left shows the probability density function. The right shows the cumulative distribution function, for which the value at '''a''' equals the area under the probability density curve to the left of '''a'''.]]
+
== Distribution Functions for Random Variables ==
−
Absolutely continuous probability distributions can be described in several ways. The [[probability density function]] describes the [[infinitesimal]] probability of any given value, and the probability that the outcome lies in a given interval can be computed by [[Integration (mathematics)|integrating]] the probability density function over that interval.<ref name=":3" /> An alternative description of the distribution is by means of the [[cumulative distribution function]], which describes the probability that the random variable is no larger than a given value (i.e., <math>P(X < x)</math> for some <math>x</math>). The cumulative distribution function is the area under the [[probability density function]] from <math>-\infty</math> to <math>x</math>, as described by the picture to the right.<ref name='dekking'>{{Cite book|title=A modern introduction to probability and statistics : understanding why and how|date=2005|publisher=Springer|others=Dekking, Michel, 1946-|isbn=978-1-85233-896-1|location=London|oclc=262680588}}</ref>
+
The distribution function provides important information about the probabilities associated with different values of a random variable. It can be used to calculate probabilities for specific events or to obtain other statistical properties of the random variable. <ref name="probz">Spiegel, M. R., Schiller, J. T., & Srinivasan, A. <i>Probability and Statistics : based on Schaum’s outline of Probability and Statistics</i>, published 2001 https://ci.nii.ac.jp/ncid/BA77714681</ref>
  
−
==General probability definition==
+
*It gives the probability that the random variable takes on a value less than or equal to a given value.
 +
The distribution function of a random variable X, denoted as '''F(x)''', is defined as: <ref name="probz">Spiegel, M. R., Schiller, J. T., & Srinivasan, A. <i>Probability and Statistics : based on Schaum’s outline of Probability and Statistics</i>, published 2001 https://ci.nii.ac.jp/ncid/BA77714681</ref>
  
−
A probability distribution can be described in various forms, such as by a probability mass function or a cumulative distribution function. One of the most general descriptions, which applies for absolutely continuous and discrete variables, is by means of a probability function <math>P\colon \mathcal{A} \to \Reals</math> whose '''input space''' <math>\mathcal{A}</math> is a [[σ-algebra]], and gives a [[real number]] '''probability''' as its output, particulary, a number in <math>[0,1] \subseteq \Reals</math>.
+
*F(x) = P(X ≤ x)
  
−
The probability function <math>P</math> can take as argument subsets of the sample space itself, as in the coin toss example, where the function <math>P</math> was defined so that {{math|1=''P''(heads) = 0.5}} and {{math|1=''P''(tails) = 0.5}}. However, because of the widespread use of [[random variables]], which transform the sample space into a set of numbers (e.g., <math>\R</math>, <math>\N</math>), it is more common to study probability distributions whose argument are subsets of these particular kinds of sets (number sets),<ref>{{cite book| last1 = Walpole | first1 = R.E. | last2 = Myers | first2 = R.H. | last3 = Myers | first3 = S.L. | last4 = Ye | first4 = K.|year=1999|title=Probability and statistics for engineers|publisher=Prentice Hall}}</ref> and all probability distributions discussed in this article are of this type. It is common to denote as <math>P(X \in E)</math> the probability that a certain value of the variable <math>X</math> belongs to a certain event <math>E</math>.<ref name='ross' /><ref name='degroot' />
+
where x is any real number, and P(X ≤ x) is the probability that the random variable X is less than or equal to x. <ref name="probz">Spiegel, M. R., Schiller, J. T., & Srinivasan, A. <i>Probability and Statistics : based on Schaum’s outline of Probability and Statistics</i>, published 2001 https://ci.nii.ac.jp/ncid/BA77714681</ref>
  
−
The above probability function only characterizes a probability distribution if it satisfies all the [[Kolmogorov axioms]], that is:
+
=== Distribution Functions for Discrete Random Variables ===
−
# <math>P(X \in E) \ge 0 \; \forall E \in \mathcal{A}</math>, so the probability is non-negative
+
If X takes on only a finite number of values ''x1, x2, . . . , xn,'' then the distribution function is given by <br>
−
# <math>P(X \in E) \le 1 \; \forall E \in \mathcal{A}</math>, so no probability exceeds <math>1</math>
+
[[File:discreteF.png|thumb|center|[[Probability distributions#Uniform distribution - discrete|Distribution function of a discrete variable]]]]
−
# <math>P(X \in \bigcup_{i} E_i ) = \sum_i P(X \in E_i)</math> for any disjoint family of sets <math>\{ E_i \}</math>
 
  
−
The concept of probability function is made more rigorous by defining it as the element of a [[probability space]] <math>(X, \mathcal{A}, P)</math>, where <math>X</math> is the set of possible outcomes, <math>\mathcal{A}</math> is the set of all subsets <math>E \subset X</math> whose probability can be measured, and <math>P</math> is the probability function, or '''probability measure''', that assigns a probability to each of these measurable subsets <math>E \in \mathcal{A}</math>.<ref name='billingsley'>{{cite book|author1=Billingsley, P.|year=1986|title=Probability and measure| publisher=Wiley | isbn=9780471804789}}</ref>
 
  
−
Probability distributions usually belong to one of two classes. A '''discrete probability distribution''' is applicable to the scenarios where the set of possible outcomes is [[discrete probability distribution|discrete]] (e.g. a coin toss, a roll of a die) and the probabilities are encoded by a discrete list of the probabilities of the outcomes; in this case the discrete probability distribution is known as [[probability mass function]]. On the other hand, '''absolutely continuous probability distributions''' are applicable to scenarios where the set of possible outcomes can take on values in a continuous range (e.g. real numbers), such as the temperature on a given day. In the absolutely continuous case, probabilities are described by a [[probability density function]], and the probability distribution is by definition the integral of the probability density function.<ref name="ross" /><ref name=":3">{{cite web|title=1.3.6.1. What is a Probability Distribution |url=https://www.itl.nist.gov/div898/handbook/eda/section3/eda361.htm|access-date=2020-09-10 |website=www.itl.nist.gov}}</ref><ref name='degroot'>{{cite book|last1=DeGroot|first1=Morris H. |last2=Schervish|first2=Mark J.|title=Probability and Statistics|publisher=Addison-Wesley|year=2002}}</ref> The [[normal distribution]] is a commonly encountered absolutely continuous probability distribution. More complex experiments, such as those involving [[stochastic processes]] defined in [[continuous time]], may demand the use of more general [[probability measure]]s.
+
==== Example ====
 +
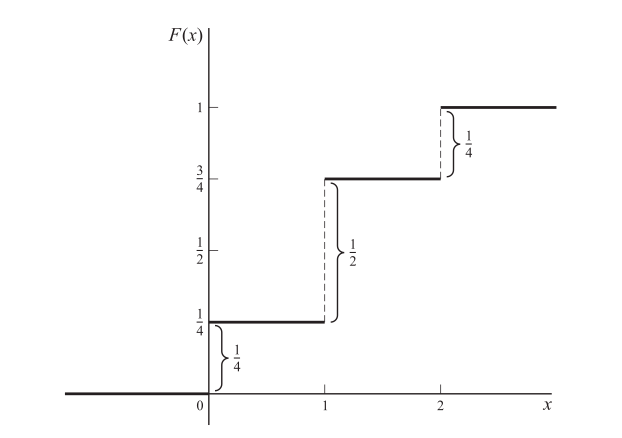
The following function: [[File:discreteEx.png|thumb|center]]
 +
Can be graphed as follows: [[File:Grafdiscrete.png|center]]
  
−
A probability distribution whose sample space is one-dimensional (for example real numbers, list of labels, ordered labels or binary) is called [[Univariate distribution|univariate]], while a distribution whose sample space is a [[vector space]] of dimension 2 or more is called [[Multivariate distribution|multivariate]]. A univariate distribution gives the probabilities of a single [[random variable]] taking on various different values; a multivariate distribution (a [[joint probability distribution]]) gives the probabilities of a [[random vector]] – a list of two or more random variables – taking on various combinations of values. Important and commonly encountered univariate probability distributions include the [[binomial distribution]], the [[hypergeometric distribution]], and the [[normal distribution]]. A commonly encountered multivariate distribution is the [[multivariate normal distribution]].
+
#The magnitudes of the jumps  are 1/4, 1/2, 1/4 which are precisely the probabilities from the function. This fact enables one to obtain the probability function from the distribution function.
 +
# Because of the appearance of the graph it is often called a ''staircase function'' or ''step function''.
 +
#The value of the function at an integer is obtained from the higher step; thus the value at 1 is 4 and not 4. This is expressed mathematically by stating that the distribution function is continuous from the right at 0, 1, 2. 3. As we proceed from left to right (i.e. going upstairs), the distribution function either remains the same or increases, taking on values from 0 to 1. Because of this, it is said to be a monotonically increasing function.
  
−
Besides the probability function, the cumulative distribution function, the probability mass function and the probability density function, the [[moment generating function]] and the [[characteristic function (probability theory)|characteristic function]] also serve to identify a probability distribution, as they uniquely determine an underlying cumulative distribution function.<ref>{{cite journal|author1=Shephard, N.G.|year=1991|title=From characteristic function to distribution function: a simple framework for the theory|journal=Econometric Theory|volume=7|issue=4|pages=519–529|doi=10.1017/S0266466600004746|s2cid=14668369 |url=https://ora.ox.ac.uk/objects/uuid:a4c3ad11-74fe-458c-8d58-6f74511a476c}}</ref>
+
=== Distribution Functions for Continuous Variables ===
−
[[File:Standard deviation diagram.svg|right|thumb|250px|The [[probability density function]] (pdf) of the [[normal distribution]], also called Gaussian or "bell curve", the most important absolutely continuous random distribution. As notated on the figure, the probabilities of intervals of values correspond to the area under the curve.]]
+
* A nondiscrete random variable X is said to be absolutely continuous, or simply continuous, if its distribution function may be represented as
 +
[[File:cont.png|center]]
  
−
== Terminology ==
+
* where the function ''f(x)'' has the properties
 +
[[File:contprop.png|center]]
 +
 
 +
* The graphical representation of a possible probability distribution function (PDF) ''f(x)'' and it's cumulative distribution function (CDF) ''F(x)'' is given by the graph bellow:
 +
[[File:graphcont.png|center]]
  
−
Some key concepts and terms, widely used in the literature on the topic of probability distributions, are listed below.<ref name=":02" />
+
== Special Probability Distributions ==
  
−
=== Basic terms ===
+
=== The Uniform Distribution ===
−
*''[[Random variable]]'': takes values from a sample space; probabilities describe which values and set of values are taken more likely.
+
A continuous random variable ''X'' is said to have a '''Uniform''' distribution over the interval [a,b], shown as ''X ∼ Uniform(a,b)'', if its PDF is given by <ref name="probiz"> Pishro-Nik, H.  <i> Introduction to Probability, Statistics, and Random Processes</i>, published 2014, https://www.probabilitycourse.com/preface.php</ref>
−
*''[[Event (probability theory)|Event]]'': set of possible values (outcomes) of a random variable that occurs with a certain probability.
+
[[File:unifun.png|center]]
−
*''[[Probability measure|Probability function]]'' or ''probability measure'': describes the probability <math>P(X \in E)</math> that the event <math>E,</math> occurs.<ref name='vapnik'>Chapters 1 and 2 of {{harvp|Vapnik|1998}}</ref>
+
The '''expected value''' is therefore
−
*''[[Cumulative distribution function]]'': function evaluating the [[probability]] that <math>X</math> will take a value less than or equal to <math>x</math> for a random variable (only for real-valued random variables).
+
[[File:uniex.png|center]]
−
*''[[Quantile function]]'': the inverse of the cumulative distribution function. Gives <math>x</math> such that, with probability <math>q</math>, <math>X</math> will not exceed <math>x</math>.
+
and '''variance'''
 +
[[File:univar.png|center]]
  
−
=== Discrete probability distributions ===
+
==== Example ====
−
*'''Discrete probability distribution''': for many random variables with finitely or countably infinitely many values.
+
* When you flip a coin, the probability of the coin landing with a head faced up is equal to the probability that it lands with a tail faced up.  
−
*''[[Probability mass function]]'' (''pmf''): function that gives the probability that a discrete random variable is equal to some value.
+
* When a fair die is rolled, the probability that the number appearing on the top of the die lies in between one to six follows a uniform distribution. The probability that any number will appear on the top of the die is equal to 1/6.
−
*''[[Frequency distribution]]'': a table that displays the frequency of various outcomes {{em|in a sample}}.
 
−
*''[[Relative frequency]] distribution'': a [[frequency distribution]] where each value has been divided (normalized) by a number of outcomes in a [[Sample (statistics)|sample]] (i.e. sample size).
 
−
*''[[Categorical distribution]]'': for discrete random variables with a finite set of values.
 
  
−
=== Absolutely continuous probability distributions ===
+
=== The Normal Distribution ===
−
*'''Absolutely continuous probability distribution''': for many random variables with uncountably many values.
+
The '''normal distribution''' is by far the most important probability distribution. One of the main reasons for that is the Central Limit Theorem (CLT)
−
*''[[Probability density function]]'' (''pdf'') or ''probability density'': function whose value at any given sample (or point) in the [[sample space]] (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would equal that sample.
+
* The notation for the random variable is written as ''X ∼ N(􏰏μ,σ)''.
 +
* 􏰏Also called the '''Gaussian''' distribution, the density function for this distribution is given by
 +
[[File:normf.png|center]]
 +
where 􏰏μ􏰏 a􏰏􏰏nd σ are the mean and standard deviation, respectively.
  
−
=== Related terms ===
+
* Let Z be the standardized variable corresponding to X
−
*[[Support (mathematics)|''Support'']]: set of values that can be assumed with non-zero probability by the random variable. For a random variable <math>X</math>, it is sometimes denoted as <math>R_X</math>.
+
[[File:normz.png|center]]
−
*'''Tail''':<ref name='tail'>More information and examples can be found in the articles [[Heavy-tailed distribution]], [[Long-tailed distribution]], [[fat-tailed distribution]]</ref> the regions close to the bounds of the random variable, if the pmf or pdf are relatively low therein. Usually has the form <math>X > a</math>, <math>X < b</math> or a union thereof.
 
−
*'''Head''':<ref name='tail' /> the region where the pmf or pdf is relatively high. Usually has the form <math>a < X < b</math>.
 
−
*''[[Expected value]]'' or ''mean'': the [[weighted average]] of the possible values, using their probabilities as their weights; or the continuous analog thereof.
 
−
*''[[Median]]'': the value such that the set of values less than the median, and the set greater than the median, each have probabilities no greater than one-half.
 
−
*[[Mode (statistics)|''Mode'']]: for a discrete random variable, the value with highest probability; for an absolutely continuous random variable, a location at which the probability density function has a local peak.
 
−
*''[[Quantile]]'': the q-quantile is the value <math>x</math> such that <math>P(X < x) = q</math>.
 
−
*''[[Variance]]'': the second moment of the pmf or pdf about the mean; an important measure of the [[Statistical dispersion|dispersion]] of the distribution.
 
−
*''[[Standard deviation]]'': the square root of the variance, and hence another measure of dispersion.
 
−
*[[Symmetric probability distribution|''Symmetry'']]: a property of some distributions in which the portion of the distribution to the left of a specific value (usually the median) is a mirror image of the portion to its right.
 
−
*''[[Skewness]]'': a measure of the extent to which a pmf or pdf "leans" to one side of its mean. The third [[standardized moment]] of the distribution.
 
−
*''[[Kurtosis]]'': a measure of the "fatness" of the tails of a pmf or pdf. The fourth standardized moment of the distribution.
 
  
−
==Cumulative distribution function==
 
−
In the special case of a real-valued random variable, the probability distribution can equivalently be represented by a cumulative distribution function instead of a probability measure. The cumulative distribution function of a random variable <math>X</math> with regard to a probability distribution <math>p</math> is defined as
 
−
<math display="block">F(x) = P(X \leq x).</math>
 
  
−
The cumulative distribution function of any real-valued random variable has the properties:
+
==== Some Properties of the Normal Distribution ====
−
*<li style="margin: 0.7rem 0;"><math>F(x)</math> is non-decreasing;</li>
+
[[File:normprop.png|center]]
−
*<li style="margin: 0.7rem 0;"><math>F(x)</math> is [[right-continuous]];</li>
 
−
*<li style="margin: 0.7rem 0;"><math>0 \le F(x) \le 1</math>;</li>
 
−
*<li style="margin: 0.7rem 0;"><math>\lim_{x \to -\infty} F(x) = 0</math> and <math>\lim_{x \to \infty} F(x) = 1</math>; and</li>
 
−
*<li style="margin: 0.7rem 0;"><math>\Pr(a < X \le b) = F(b) - F(a)</math>.</li>
 
  
−
Conversely, any function <math>F:\mathbb{R}\to\mathbb{R}</math> that satisfies the first four of the properties above is the cumulative distribution function of some probability distribution on the real numbers.<ref>{{Cite book|title=Probability and stochastics|last=Erhan|first=Çınlar|date=2011|publisher=Springer|isbn=9780387878584|location=New York|pages=57}}</ref>
+
==== Graphical representation ====
 +
A graph of the density function, sometimes called the '''standard normal curve'''. The areas within 1, 2, and 3 standard deviations of the mean are indicated.
 +
[[File:normgrafh.png|center]]
  
−
Any probability distribution can be decomposed as the [[mixture distribution|mixture]] of a [[Discrete probability distribution|discrete]], an [[Absolutely continuous probability distribution|absolutely continuous]] and a [[Singular measure|singular continuous distribution]],<ref>see [[Lebesgue's decomposition theorem]]</ref> and thus any cumulative distribution function admits a decomposition as the [[convex sum]] of the three according cumulative distribution functions.
+
==== Central Limit Theorem (CLT) ====
 +
The central limit theorem (CLT) is one of '''the most important results in probability theory'''. It tells us that, under certain conditions, the sum of a large number of random variables is approximately normal.
  
−
==Discrete probability distribution==
+
The central limit theorem states that if you have a population with mean μ and standard deviation σ and take sufficiently large random samples from the population with replacement, then the distribution of the sample means will be approximately normally distributed. This will hold true regardless of whether the source population is normal or skewed, provided the sample size is sufficiently large (usually '''n > 30'''). If the population is normal, then the theorem holds true even for samples smaller than 30.
−
{{Main|Probability mass function}}
 
  
−
[[File:Discrete probability distrib.svg|right|thumb|The probability mass function of a discrete probability distribution. The probabilities of the [[Singleton (mathematics)|singleton]]s {1}, {3}, and {7} are respectively 0.2, 0.5, 0.3. A set not containing any of these points has probability zero.]]
+
=== The Binomial Distributions ===
−
[[File:Discrete probability distribution.svg|right|thumb|The [[cumulative distribution function|cdf]] of a discrete probability distribution, ...]]
+
* Suppose that we have an experiment such as tossing a coin repeatedly or choosing a marble from an urn repeatedly.
−
[[File:Normal probability distribution.svg|right|thumb|... of a continuous probability distribution, ...]]
+
* Each toss or selection is called a ''trial''.  
−
[[File:Mixed probability distribution.svg|right|thumb|... of a distribution which has both a continuous part and a discrete part.]]
+
*In any single trial there will be a probability associated with a particular event such as head on the coin, 4 on the die, or selection of a red marble. In some cases this probability will not change from one trial to the next (as in tossing a coin or die).  
 +
* Such trials are then said to be independent and are often called Bernoulli trials after James Bernoulli who investigated them at the end of the seventeenth century.
 +
* If ''n'' is large and if neither ''p'' nor ''q'' is too close to zero, the binomial distribution can be closely approximated by a normal distribution.
  
−
A '''discrete probability distribution''' is the probability distribution of a random variable that can take on only a countable number of values<ref>{{Cite book|title=Probability and stochastics|last=Erhan|first=Çınlar|date=2011|publisher=Springer| isbn=9780387878591| location=New York|pages=51|oclc=710149819}}</ref> ([[almost surely]])<ref>{{Cite book|title=Measure theory| last=Cohn|first=Donald L.|date=1993|publisher=Birkhäuser}}</ref> which means that the probability of any event <math>E</math> can be expressed as a (finite or [[Series (mathematics)|countably infinite]]) sum:
 
−
<math display="block">P(X\in E) = \sum_{\omega\in A \cap E} P(X = \omega),</math>
 
−
where <math>A</math> is a countable set with <math>P(X \in A) = 1</math>. Thus the discrete random variables are exactly those with a [[probability mass function]] <math>p(x) = P(X=x)</math>. In the case where the range of values is countably infinite, these values have to decline to zero fast enough for the probabilities to add up to 1. For example, if <math>p(n) = \tfrac{1}{2^n}</math> for <math>n = 1, 2, ...</math>, the sum of probabilities would be <math>1/2 + 1/4 + 1/8 + \dots = 1</math>.
 
  
−
A '''discrete random variable''' is a random variable whose probability distribution is discrete.
+
Let ''p'' be the probability that an event will happen in any single Bernoulli trial (called the probability of success). Then q 􏰂 1 􏰁 p is the probability that the event will fail to happen in any single trial (called the probability of failure). The probability that the event will happen exactly x times in n trials (i.e., successes and n 􏰁 x failures will occur) is given by the probability function
 +
[[File:binom.png|center]]
  
−
Well-known discrete probability distributions used in statistical modeling include the [[Poisson distribution]], the [[Bernoulli distribution]], the [[binomial distribution]], the [[geometric distribution]], the [[negative binomial distribution]] and [[categorical distribution]].<ref name=":1" /> When a [[Sample (statistics)|sample]] (a set of observations) is drawn from a larger population, the sample points have an [[empirical distribution function|empirical distribution]] that is discrete, and which provides information about the population distribution. Additionally, the [[Uniform distribution (discrete)|discrete uniform distribution]] is commonly used in computer programs that make equal-probability random selections between a number of choices.
+
The key characteristics of a binomial distribution are as follows:
 +
# The trials are independent: The outcome of each trial does not depend on the outcome of any other trial.
 +
# Each trial has two possible outcomes: success or failure.
 +
# The probability of success remains constant across all trials, denoted as ''p''.
 +
# The number of trials is fixed, denoted as ''n''.
  
−
===Cumulative distribution function===
+
'''Some Properties of Binomial Distribution'''
−
A real-valued discrete random variable can equivalently be defined as a random variable whose cumulative distribution function increases only by [[jump discontinuity|jump discontinuities]]—that is, its cdf increases only where it "jumps" to a higher value, and is constant in intervals without jumps. The points where jumps occur are precisely the values which the random variable may take.
+
[[File:binomprop.png|center]]
−
Thus the cumulative distribution function has the form
 
−
<math display="block">F(x) = P(X \leq x) = \sum_{\omega \leq x} p(\omega).</math>
 
  
−
The points where the cdf jumps always form a countable set; this may be any countable set and thus may even be dense in the real numbers.
+
==== Example ====
 +
The probability of getting exactly 2 heads in 6 tosses of a fair coin is:
 +
[[File:binomEx.png|center]]
  
−
===Dirac delta representation===
+
=== The Bernoulli Distribution ===
−
A discrete probability distribution is often represented with [[Dirac measure]]s, the probability distributions of [[Degenerate distribution|deterministic random variable]]s. For any outcome <math>\omega</math>, let <math>\delta_\omega</math> be the Dirac measure concentrated at <math>\omega</math>. Given a discrete probability distribution, there is a countable set <math>A</math> with <math>P(X \in A) = 1</math> and a probability mass function <math>p</math>. If <math>E</math> is any event, then
+
*Bernoulli distributions arise anytime we have a response variable that takes only two possible values, and we label one of these outcomes as 1 and the other as 0.
−
<math display="block">P(X \in E) = \sum_{\omega \in A} p(\omega) \delta_\omega(E),</math> or in short, <math display="block">P_X = \sum_{\omega \in A} p(\omega) \delta_\omega.</math>
+
* For example, 1 could correspond to success and 0 to failure of some quality test applied to an item produced in a manufacturing process.
 +
* Alternatively, we could be randomly selecting an individual from a population and recording a 1 when the individual is female and a 0 if the individual is a male. In this case, θ is the proportion of females in the population.
 +
*The binomial distribution is applicable to any situation involving ''n'' independent performances of a random system; for each performance, we are recording whether a particular event has occurred, called a ''success'', or has not occurred, called a ''failure''.
 +
==== Difference between the Binomial and Bernoulli Distribution ====
 +
*The binomial distribution is derived from multiple independent Bernoulli trials. It represents the number of successes in these trials.
 +
*Each trial in the binomial distribution follows a Bernoulli distribution.
 +
*The Bernoulli distribution models a single trial with two possible outcomes, while the binomial distribution models the number of successes in a fixed number of independent Bernoulli trials. The binomial distribution extends the concept of the Bernoulli distribution to multiple trials.
  
−
Similarly, discrete distributions can be represented with the [[Dirac delta function]] as a [[Generalized function|generalized]] [[probability density function]] <math>f</math>, where <math display="block">f(x) = \sum_{\omega \in A} p(\omega) \delta(x - \omega),</math> which means
+
=== Multinomial Distribution ===
−
<math display="block">P(X \in E) = \int_E f(x) \, dx = \sum_{\omega \in A} p(\omega) \int_E \delta(x - \omega) = \sum_{\omega \in A \cap E} p(\omega)</math> for any event <math>E.</math><ref>{{Cite journal|last=Khuri|first=André I.|date=March 2004| title=Applications of Dirac's delta function in statistics|journal=International Journal of Mathematical Education in Science and Technology| language=en|volume=35|issue=2|pages=185–195| doi=10.1080/00207390310001638313|s2cid=122501973|issn=0020-739X}}</ref>
+
Suppose that events ''A1, A2, . . . , Ak'' are mutually exclusive, and can occur with respective probabilities ''p1, p2, . . . , p'' where ''p1 + p2􏰃 + ... + pk = 1''. If ''X1 , X2 , . . . , Xk'' are the random variables respectively giving the number of times that ''A1 , A2 , . . . , A'' occur in a total of ''n'' trials, so that ''X1 + X2 + ... +􏰃 X = n'', then
 +
[[File:multinomm.png|center]]
 +
* It is a generalization of the Binomial distribution
  
−
===Indicator-function representation===
+
==== Example ====
−
For a discrete random variable <math>X</math>, let <math>u_0, u_1, \dots</math> be the values it can take with non-zero probability. Denote
+
If a fair die is to be tossed 12 times, the probability of getting 1, 2, 3, 4, 5 and 6 points exactly twice
 +
each is
 +
[[File:multinommex.png|center]]
  
−
<math display="block">\Omega_i=X^{-1}(u_i)= \{\omega: X(\omega)=u_i\},\, i=0, 1, 2, \dots</math>
+
=== The Poisson Distributions ===
 +
*Poisson distribution definition is used to model a discrete probability of an event where independent events are occurring in a fixed interval of time and have a known constant mean rate.
 +
*In other words, Poisson distribution is used to estimate how many times an event is likely to occur within the given period of time.
 +
* Poisson distribution has wide use in the fields of business as well as in biology.
  
−
These are [[disjoint set]]s, and for such sets
+
The distribution function is given by
 +
[[File:poissonfun.png|center]]
 +
where ''λ'' is the Poisson rate parameter that indicates the expected value of the average number of events in the fixed time interval.
  
−
<math display="block">P\left(\bigcup_i \Omega_i\right)=\sum_i P(\Omega_i)=\sum_i P(X=u_i)=1.</math>
+
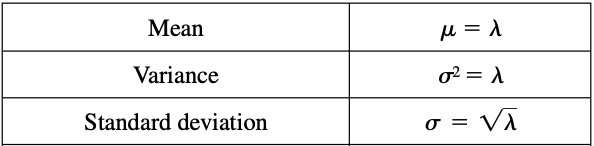
==== Some properties of Poisson distribution ====
 +
[[File:poissonprop.png|center]]
  
−
It follows that the probability that <math>X</math> takes any value except for <math>u_0, u_1, \dots</math> is zero, and thus one can write <math>X</math> as
+
==== Binomial and Poisson aproximation ====
 +
In the binomial distribution, if ''n'' is large while the probability ''p'' of occurrence of an event is close to zero, so that ''q = 1 -􏰁 p'' is close to 1, the event is called a ''rare'' event. In practice we shall consider an event as rare if the number of trials is at least 50 (n>50) while ''np'' is less than 5. For such cases the binomial distribution is very closely approximated by the Poisson distribution with ''λ􏰒 =􏰂 np''.
 +
'''Example'''
 +
* Ten percent of the tools produced in a certain manufacturing process turn out to be defective. Find the probability that in a sample of 10 tools chosen at random, exactly 2 will be defective, by using '''(1)''' the binomial distribution, '''(2)''' the Poisson approximation to the binomial distribution.
  
−
<math display="block">X(\omega)=\sum_i u_i 1_{\Omega_i}(\omega)</math>
+
# The probability of a defective tool is p 􏰂 0.1. Let ''X'' denote the number of defective tools out of 10 chosen. Then, according to the binomial distribution
 +
[[File:poissonprii.png|center]]
 +
# We have 􏰒 􏰒􏰂''λ = np = (10)(0.1)'' = 1. Then, according to the Poisson distribution,
 +
[[File:poissonpri.png|center]]
 +
*In general, the approximation is good if ''p ≤ 0.1'' and ''􏰒np 􏰀≥ 5''.
  
−
except on a set of probability zero, where <math>1_A</math> is the indicator function of <math>A</math>. This may serve as an alternative definition of discrete random variables.
+
=== The Exponential Distribution ===
 +
The exponential distribution is one of the widely used continuous distributions. It is often used to model the time elapsed between events. <ref name="probiz"> Pishro-Nik, H.  <i> Introduction to Probability, Statistics, and Random Processes</i>, published 2014, https://www.probabilitycourse.com/preface.php</ref>  
  
−
===One-point distribution===
+
* It is defined by: <ref name="probzz"> Evans, M. J., & Rosenthal, J. S.<i>Probability and Statistics: The Science of Uncertainty</i>, published 2009, WH Freeman. </ref>
−
+
[[File:exponentialol.png|center]]
−
A special case is the discrete distribution of a random variable that can take on only one fixed value; in other words, it is a [[deterministic distribution]]. Expressed formally, the random variable <math>X</math> has a one-point distribution if it has a possible outcome <math>x</math> such that <math>P(X{=}x)=1.</math><ref>{{cite book |title=Probability Theory and Mathematical Statistics |first=Marek |last=Fisz |edition=3rd |publisher=John Wiley & Sons |year=1963 |isbn=0-471-26250-1 |page=129}}</ref> All other possible outcomes then have probability 0. Its cumulative distribution function jumps immediately from 0 to 1.
 
  
−
== Absolutely continuous probability distribution==
+
* An exponential distribution can often be used to model lifelengths. For example, a certain type of light bulb produced by a manufacturer might follow an ''Exponential(λ)'' distribution for an appropriate choice of ''λ''. The lifelength ''X'' of a randomly selected light bulb from those produced by this manufacturer has probability of lasting longer than ''x'' units of time can be calculated by following:<ref name="probzz"> Evans, M. J., & Rosenthal, J. S.<i>Probability and Statistics: The Science of Uncertainty</i>, published 2009, WH Freeman. </ref>
−
{{Main|Probability density function}}
+
[[File:exponentialoll.png|center]]
  
−
An '''absolutely continuous probability distribution''' is a probability distribution on the real numbers with uncountably many possible values, such as a whole interval in the real line, and where the probability of any event can be expressed as an integral.<ref>{{Cite book|title=A First Look at Rigorous Probability Theory|author1=Jeffrey Seth Rosenthal|date=2000| publisher=World Scientific}}</ref> More precisely, a real random variable <math>X</math> has an [[absolutely continuous]] probability distribution if there is a function <math>f: \Reals \to [0, \infty]</math> such that for each interval <math>[a,b] \subset \mathbb{R}</math> the probability of <math>X</math> belonging to <math>[a,b]</math> is given by the integral of <math>f</math> over <math>I</math>:<ref>Chapter 3.2 of {{harvp|DeGroot|Schervish|2002}}</ref><ref>{{Cite web| last=Bourne|first=Murray|title=11. Probability Distributions - Concepts|url=https://www.intmath.com/counting-probability/11-probability-distributions-concepts.php|access-date=2020-09-10|website=www.intmath.com|language=en-us}}</ref>
+
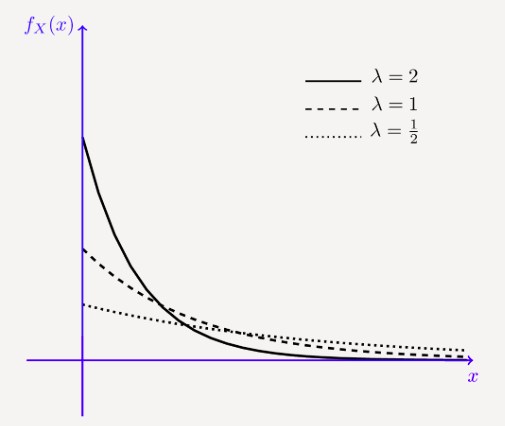
* The graph of the ''Exponential(λ)'' distribution depends on the ''λ'' paramater: <ref name="probzz"> Evans, M. J., & Rosenthal, J. S.<i>Probability and Statistics: The Science of Uncertainty</i>, published 2009, WH Freeman. </ref>
−
<math display="block">P\left(a \le X \le b \right) = \int_a^b f(x) \, dx .</math>
+
[[File:exponentiagraph.png|center]]
−
This is the definition of a [[probability density function]], so that absolutely continuous probability distributions are exactly those with a probability density function.
 
−
In particular, the probability for <math>X</math> to take any single value <math>a</math> (that is, <math>a \le X \le a</math>) is zero, because an [[integral]] with coinciding upper and lower limits is always equal to zero.
 
−
If the interval <math>[a,b]</math> is replaced by any measurable set <math>A</math>, the according equality still holds:
 
−
<math display="block"> P(X \in A) = \int_A f(x) \, dx .</math>
 
  
−
An '''absolutely continuous random variable''' is a random variable whose probability distribution is absolutely continuous.
+
==== Example ====
 +
* Imagine you are at a store and are waiting for the next customer. In each millisecond, the probability that a new customer enters the store is very small. You can imagine that, in each millisecond, a coin (with a very small P(H) is tossed, and if it lands heads a new customers enters. If you toss a coin every millisecond, the time until a new customer arrives approximately follows an exponential distribution.<ref name="probiz"> Pishro-Nik, H.  <i> Introduction to Probability, Statistics, and Random Processes</i>, published 2014, https://www.probabilitycourse.com/preface.php</ref>
  
−
There are many examples of absolutely continuous probability distributions: [[normal distribution|normal]], [[Uniform distribution (continuous)|uniform]], [[Chi-squared distribution|chi-squared]], and [[List of probability distributions#Absolutely continuous distributions|others]].
+
=== The Gamma Distribution ===
 +
The gamma function is defined by
 +
[[File:gammafun.png|center]]
 +
where,  
 +
[[File:gammafunnz.png|center]]
  
−
=== Cumulative distribution function ===
+
* For the case α = 1 corresponds to the Exponential(λ) distribution: Gamma(1, λ) = Exponential(λ) <ref name="probzz"> Evans, M. J., & Rosenthal, J. S.<i>Probability and Statistics: The Science of Uncertainty</i>, published 2009, WH Freeman. </ref>
−
Absolutely continuous probability distributions as defined above are precisely those with an [[Absolute continuity|absolutely continuous]] cumulative distribution function.
 
−
In this case, the cumulative distribution function <math>F</math> has the form
 
−
<math display="block">F(x) = P(X \leq x) = \int_{-\infty}^x f(t)\,dt</math>
 
−
where <math>f</math> is a density of the random variable <math>X</math> with regard to the distribution <math>P</math>.
 
  
−
''Note on terminology:'' Absolutely continuous distributions ought to be distinguished from '''continuous distributions''', which are those having a continuous cumulative distribution function. Every absolutely continuous distribution is a continuous distribution but the inverse is not true, there exist [[singular distribution]]s, which are neither absolutely continuous nor discrete nor a mixture of those, and do not have a density. An example is given by the [[Cantor distribution]]. Some authors however use the term "continuous distribution" to denote all distributions whose cumulative distribution function is [[absolutely continuous function|absolutely continuous]], i.e. refer to absolutely continuous distributions as continuous distributions.<ref name="ross">{{cite book|first=Sheldon M.|last=Ross|title=A first course in probability|publisher=Pearson|year=2010}}</ref>  
+
==== Example ====
 +
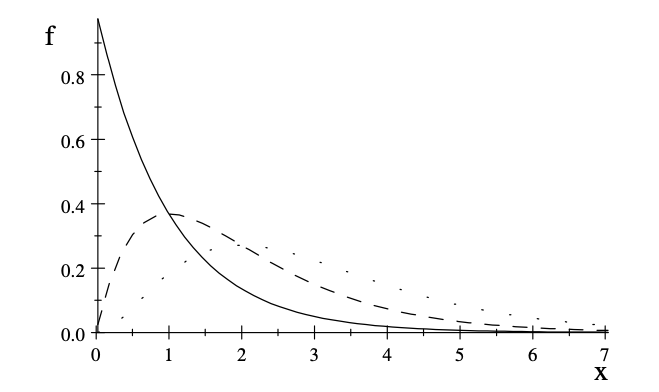
In the following graph, we can see the ''Exponential distribution'' function (solid line) and the ''Gamma function'' (dotted line) plotted:<ref name="probzz"> Evans, M. J., & Rosenthal, J. S.<i>Probability and Statistics: The Science of Uncertainty</i>, published 2009, WH Freeman. </ref>
 +
[[File:gammafunynz.png|center]]
  
−
For a more general definition of density functions and the equivalent absolutely continuous measures see [[absolutely continuous measure]].
+
== References ==
 +
<references/>

Latest revision as of 19:06, 1 June 2023

In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. In any random experiment there is always uncertainty as to whether a particular event will or will not occur. As a measure of the chance, or probability, with which we can expect the event to occur, it is convenient to assign a number between 0 and 1. [1]


Introduction

Probability is the science of uncertainty. It provides precise mathematical rules for understanding and analyzing our own ignorance. It does not tell us tomorrow’s weather or next week’s stock prices; rather, it gives us a framework for working with our limited knowledge and for making sensible decisions based on what we do and do not know.[2]

Terminology

Sample space

In probability theory, the sample space refers to the set of all possible outcomes of a random experiment. It is denoted by the symbol Ω (capital omega).[3]

  • Let's consider an example of rolling a fair six-sided die. The sample space in this case would be {1, 2, 3, 4, 5, 6}, as these are the possible outcomes of the experiment. Each number represents the face of the die that may appear when it is rolled. [3]

Random variable

Random variable takes values from a sample space. In contrast, probabilities describe which values and set of values are more likely to be taken out of the sample space. Random variable must be quantified, therefore, it assigns a numerical value to each possible outcome in the sample space. [2]

  • For example, if the sample space for flipping a coin is {heads, tails}, then we can assign a random variable Y such that Y = 1 when heads land and Y = 0 when tails land. However, we can assign any number for these variables. 0 and 1 are just more convenient. [2]
  • Because random variables are defined to be functions of the outcome s, and because the outcome s is assumed to be random (i.e., to take on different values with different probabilities), it follows that the value of a random variable will itself be random (as the name implies).

Specifically, if X is a random variable, then what is the probability that X will equal some particular value x? Well, X = x precisely when the outcome s is chosen such that X(s) = x.

  • Exercise
    • Suppose that a coin is tossed twice so that the sample space is S = {HH, HT, TH, TT}. Let X represent the number of heads that can come up. With each sample point we can associate a number for X as shown in Table 1. Thus, for example, in the case of HH (i.e., 2 heads), X = 2 while for TH (1 head), X 􏰂= 1. It follows that X is a random variable. [2]
Table 1. Sample Space

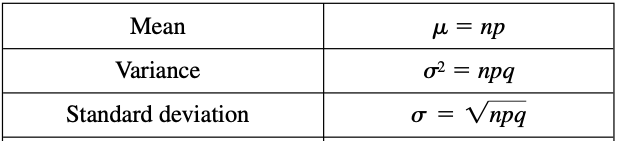
Expected value

A very important concept in probability is that of the expected value of a random variable. For a discrete random variable X having the possible values x1, c, xn, the expectation of X is defined as: [2]

Ex.png

For a continuous random variable X having density function f(x), the expectation of X is defined as

Excont.png

Example

Suppose that a game is to be played with a single die assumed fair. In this game a player wins $20 if a 2 turns up, $40 if a 4 turns up; loses $30 if a 6 turns up; while the player neither wins nor loses if any other face turns up. Find the expected sum of money to be won.

Exex.png

Variance and standard deviation

Another important quantity in probability is called the variance defined by:

Var.png

The variance is a nonnegative number. The positive square root of the variance is called the standard deviation and is given by

Standdev.png
  • If X is a discrete random variable taking the values x1, x2, . . . , xn and having probability function f(x), then the variance is given by
Vardisc.png
  • If X is a continuous random variable having density function f(x), then the variance is given by
Varcont.png
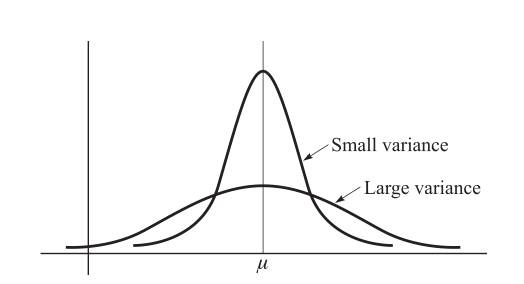
  • Graphical representation of variance for 2 continuous distribution with the same mean μ can be seen in a graph bellow
Vargraph.png

PMF vs. PDF vs. CDF

In probability theory there are 3 functions that might be little confusing for some people. Let's make the differences clear.

Pdf.png

Probability mass function (PMF)

  • The probability mass function, denoted as P(X = x), is used for discrete random variables. It assigns probabilities to each possible value that the random variable can take. The PMF gives the probability that the random variable equals a specific value.

Cumulative distribution function (CDF)

  • The cumulative distribution function, denoted as F(x), describes the probability that a random variable takes on a value less than or equal to a given value x. It gives the cumulative probability up to a specific point.
  • Since the PDF is the derivative of the CDF, the CDF can be obtained from PDF by integration

Probability density function (PDF)

To determine the distribution of a discrete random variable we can either provide its PMF or CDF. For continuous random variables, the CDF is well-defined so we can provide the CDF. However, the PMF does not work for continuous random variables, because for a continuous random variable P(X=x)=0 for all x ∈ ℝ.

  • Instead, we can usually define the probability density function (PDF). The PDF is the density of probability rather than the probability mass. The concept is very similar to mass density in physics: its unit is probability per unit length. [1]
  • The probability density function (PDF) is a function used to describe the probability distribution of a continuous random variable. Unlike discrete random variables, which have a countable set of possible values, continuous random variables can take on any value within a specified range. [1]
  • The PDF, denoted as f(x), represents the density of the probability distribution of a continuous random variable at a given point x. It provides information about the likelihood of the random variable taking on a specific value or falling within a specific range of values.
  • Since the PDF is the derivative of the CDF, the CDF can be obtained from PDF by integration [1]
Statszz.png

Distribution Functions for Random Variables

The distribution function provides important information about the probabilities associated with different values of a random variable. It can be used to calculate probabilities for specific events or to obtain other statistical properties of the random variable. [1]

  • It gives the probability that the random variable takes on a value less than or equal to a given value.

The distribution function of a random variable X, denoted as F(x), is defined as: [1]

  • F(x) = P(X ≤ x)

where x is any real number, and P(X ≤ x) is the probability that the random variable X is less than or equal to x. [1]

Distribution Functions for Discrete Random Variables

If X takes on only a finite number of values x1, x2, . . . , xn, then the distribution function is given by

Distribution function of a discrete variable


Example

The following function:

DiscreteEx.png

Can be graphed as follows:

Grafdiscrete.png
  1. The magnitudes of the jumps are 1/4, 1/2, 1/4 which are precisely the probabilities from the function. This fact enables one to obtain the probability function from the distribution function.
  2. Because of the appearance of the graph it is often called a staircase function or step function.
  3. The value of the function at an integer is obtained from the higher step; thus the value at 1 is 4 and not 4. This is expressed mathematically by stating that the distribution function is continuous from the right at 0, 1, 2. 3. As we proceed from left to right (i.e. going upstairs), the distribution function either remains the same or increases, taking on values from 0 to 1. Because of this, it is said to be a monotonically increasing function.

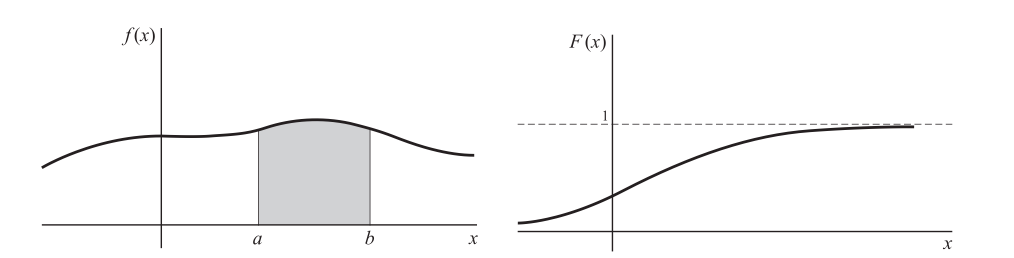
Distribution Functions for Continuous Variables

  • A nondiscrete random variable X is said to be absolutely continuous, or simply continuous, if its distribution function may be represented as
Cont.png
  • where the function f(x) has the properties
Contprop.png
  • The graphical representation of a possible probability distribution function (PDF) f(x) and it's cumulative distribution function (CDF) F(x) is given by the graph bellow:
Graphcont.png

Special Probability Distributions

The Uniform Distribution

A continuous random variable X is said to have a Uniform distribution over the interval [a,b], shown as X ∼ Uniform(a,b), if its PDF is given by [4]

Unifun.png

The expected value is therefore

Uniex.png

and variance

Univar.png

Example

  • When you flip a coin, the probability of the coin landing with a head faced up is equal to the probability that it lands with a tail faced up.
  • When a fair die is rolled, the probability that the number appearing on the top of the die lies in between one to six follows a uniform distribution. The probability that any number will appear on the top of the die is equal to 1/6.

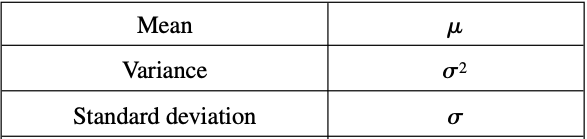
The Normal Distribution

The normal distribution is by far the most important probability distribution. One of the main reasons for that is the Central Limit Theorem (CLT)

  • The notation for the random variable is written as X ∼ N(􏰏μ,σ).
  • 􏰏Also called the Gaussian distribution, the density function for this distribution is given by
Normf.png

where 􏰏μ􏰏 a􏰏􏰏nd σ are the mean and standard deviation, respectively.

  • Let Z be the standardized variable corresponding to X
Normz.png


Some Properties of the Normal Distribution

Normprop.png

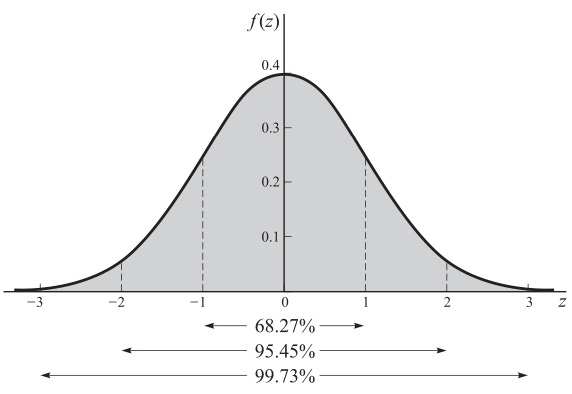
Graphical representation

A graph of the density function, sometimes called the standard normal curve. The areas within 1, 2, and 3 standard deviations of the mean are indicated.

Normgrafh.png

Central Limit Theorem (CLT)

The central limit theorem (CLT) is one of the most important results in probability theory. It tells us that, under certain conditions, the sum of a large number of random variables is approximately normal.

The central limit theorem states that if you have a population with mean μ and standard deviation σ and take sufficiently large random samples from the population with replacement, then the distribution of the sample means will be approximately normally distributed. This will hold true regardless of whether the source population is normal or skewed, provided the sample size is sufficiently large (usually n > 30). If the population is normal, then the theorem holds true even for samples smaller than 30.

The Binomial Distributions

  • Suppose that we have an experiment such as tossing a coin repeatedly or choosing a marble from an urn repeatedly.
  • Each toss or selection is called a trial.
  • In any single trial there will be a probability associated with a particular event such as head on the coin, 4 on the die, or selection of a red marble. In some cases this probability will not change from one trial to the next (as in tossing a coin or die).
  • Such trials are then said to be independent and are often called Bernoulli trials after James Bernoulli who investigated them at the end of the seventeenth century.
  • If n is large and if neither p nor q is too close to zero, the binomial distribution can be closely approximated by a normal distribution.


Let p be the probability that an event will happen in any single Bernoulli trial (called the probability of success). Then q 􏰂 1 􏰁 p is the probability that the event will fail to happen in any single trial (called the probability of failure). The probability that the event will happen exactly x times in n trials (i.e., successes and n 􏰁 x failures will occur) is given by the probability function

Binom.png

The key characteristics of a binomial distribution are as follows:

  1. The trials are independent: The outcome of each trial does not depend on the outcome of any other trial.
  2. Each trial has two possible outcomes: success or failure.
  3. The probability of success remains constant across all trials, denoted as p.
  4. The number of trials is fixed, denoted as n.

Some Properties of Binomial Distribution

Binomprop.png

Example

The probability of getting exactly 2 heads in 6 tosses of a fair coin is:

BinomEx.png

The Bernoulli Distribution

  • Bernoulli distributions arise anytime we have a response variable that takes only two possible values, and we label one of these outcomes as 1 and the other as 0.
  • For example, 1 could correspond to success and 0 to failure of some quality test applied to an item produced in a manufacturing process.
  • Alternatively, we could be randomly selecting an individual from a population and recording a 1 when the individual is female and a 0 if the individual is a male. In this case, θ is the proportion of females in the population.
  • The binomial distribution is applicable to any situation involving n independent performances of a random system; for each performance, we are recording whether a particular event has occurred, called a success, or has not occurred, called a failure.

Difference between the Binomial and Bernoulli Distribution

  • The binomial distribution is derived from multiple independent Bernoulli trials. It represents the number of successes in these trials.
  • Each trial in the binomial distribution follows a Bernoulli distribution.
  • The Bernoulli distribution models a single trial with two possible outcomes, while the binomial distribution models the number of successes in a fixed number of independent Bernoulli trials. The binomial distribution extends the concept of the Bernoulli distribution to multiple trials.

Multinomial Distribution

Suppose that events A1, A2, . . . , Ak are mutually exclusive, and can occur with respective probabilities p1, p2, . . . , p where p1 + p2􏰃 + ... + pk = 1. If X1 , X2 , . . . , Xk are the random variables respectively giving the number of times that A1 , A2 , . . . , A occur in a total of n trials, so that X1 + X2 + ... +􏰃 X = n, then

Multinomm.png
  • It is a generalization of the Binomial distribution

Example

If a fair die is to be tossed 12 times, the probability of getting 1, 2, 3, 4, 5 and 6 points exactly twice each is

Multinommex.png

The Poisson Distributions

  • Poisson distribution definition is used to model a discrete probability of an event where independent events are occurring in a fixed interval of time and have a known constant mean rate.
  • In other words, Poisson distribution is used to estimate how many times an event is likely to occur within the given period of time.
  • Poisson distribution has wide use in the fields of business as well as in biology.

The distribution function is given by

Poissonfun.png

where λ is the Poisson rate parameter that indicates the expected value of the average number of events in the fixed time interval.

Some properties of Poisson distribution

Poissonprop.png

Binomial and Poisson aproximation

In the binomial distribution, if n is large while the probability p of occurrence of an event is close to zero, so that q = 1 -􏰁 p is close to 1, the event is called a rare event. In practice we shall consider an event as rare if the number of trials is at least 50 (n>50) while np is less than 5. For such cases the binomial distribution is very closely approximated by the Poisson distribution with λ􏰒 =􏰂 np. Example

  • Ten percent of the tools produced in a certain manufacturing process turn out to be defective. Find the probability that in a sample of 10 tools chosen at random, exactly 2 will be defective, by using (1) the binomial distribution, (2) the Poisson approximation to the binomial distribution.
  1. The probability of a defective tool is p 􏰂 0.1. Let X denote the number of defective tools out of 10 chosen. Then, according to the binomial distribution
Poissonprii.png
  1. We have 􏰒 􏰒􏰂λ = np = (10)(0.1) = 1. Then, according to the Poisson distribution,
Poissonpri.png
  • In general, the approximation is good if p ≤ 0.1 and 􏰒np 􏰀≥ 5.

The Exponential Distribution

The exponential distribution is one of the widely used continuous distributions. It is often used to model the time elapsed between events. [4]

  • It is defined by: [2]
Exponentialol.png
  • An exponential distribution can often be used to model lifelengths. For example, a certain type of light bulb produced by a manufacturer might follow an Exponential(λ) distribution for an appropriate choice of λ. The lifelength X of a randomly selected light bulb from those produced by this manufacturer has probability of lasting longer than x units of time can be calculated by following:[2]
Exponentialoll.png
  • The graph of the Exponential(λ) distribution depends on the λ paramater: [2]
Exponentiagraph.png

Example

  • Imagine you are at a store and are waiting for the next customer. In each millisecond, the probability that a new customer enters the store is very small. You can imagine that, in each millisecond, a coin (with a very small P(H) is tossed, and if it lands heads a new customers enters. If you toss a coin every millisecond, the time until a new customer arrives approximately follows an exponential distribution.[4]

The Gamma Distribution

The gamma function is defined by

Gammafun.png

where,

Gammafunnz.png
  • For the case α = 1 corresponds to the Exponential(λ) distribution: Gamma(1, λ) = Exponential(λ) [2]

Example

In the following graph, we can see the Exponential distribution function (solid line) and the Gamma function (dotted line) plotted:[2]

Gammafunynz.png

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Spiegel, M. R., Schiller, J. T., & Srinivasan, A. Probability and Statistics : based on Schaum’s outline of Probability and Statistics, published 2001 https://ci.nii.ac.jp/ncid/BA77714681
  2. ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 Evans, M. J., & Rosenthal, J. S.Probability and Statistics: The Science of Uncertainty, published 2009, WH Freeman.
  3. ↑ 3.0 3.1 Casella, G., & Berger, R. L. Statistical Inference. , published 2021, Cengage Learning.
  4. ↑ 4.0 4.1 4.2 Pishro-Nik, H. Introduction to Probability, Statistics, and Random Processes, published 2014, https://www.probabilitycourse.com/preface.php
Retrieved from "http://www.simulace.info/index.php?title=Probability_distributions&oldid=24016"