Difference between revisions of "Mortgage Assessment"
(→Variables) |
(→Conclusion) |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 49: | Line 49: | ||
'''Premium Percentage ''' | '''Premium Percentage ''' | ||
| − | The premium percentage used here is based on a borrowers credit scores. Higher credit scores equal lower rate. A range of 10% to 40% was used. This value is a constant value. | + | The premium percentage used here is based on a borrowers credit scores. Higher credit scores equal lower rate. A range of 10% to 40% was used. This value is a constant value. |
Premium Percentage = 0.2 | Premium Percentage = 0.2 | ||
| Line 55: | Line 55: | ||
'''Insurance Per Month ''' | '''Insurance Per Month ''' | ||
| − | This is the monthly amount of insurance which forms part on monthly loan repayment amount. This is amount collected is collected in escrow accounts and paid to the insurance company periodically. | + | This is the monthly amount of insurance which forms part on monthly loan repayment amount. This is amount collected is collected in escrow accounts and paid to the insurance company periodically. |
Insurance Per Month = Insurance/12 | Insurance Per Month = Insurance/12 | ||
| Line 61: | Line 61: | ||
'''Tax Rate ''' | '''Tax Rate ''' | ||
| − | This is the property tax rate of the Czech Republic. | + | This is the property tax rate of the Czech Republic. |
Tax Rate = 0.04 | Tax Rate = 0.04 | ||
| Line 67: | Line 67: | ||
'''Tax Per Month''' | '''Tax Per Month''' | ||
| − | This is the monthly amount of tax which forms part on monthly loan repayment amount. This is amount collected is collected in escrow accounts and paid to the government periodically. | + | This is the monthly amount of tax which forms part on monthly loan repayment amount. This is amount collected is collected in escrow accounts and paid to the government periodically. |
Tax Per Month = Tax / 12 | Tax Per Month = Tax / 12 | ||
| Line 73: | Line 73: | ||
'''Value of Property''' | '''Value of Property''' | ||
| − | The is the price of the property a borrower is taking a loan to purchase. A range of 1,500,000 CZK to 10,000,000 CZK was used. This value is a constant value and the first simulation is done with 2,000,000 CZK | + | The is the price of the property a borrower is taking a loan to purchase. A range of 1,500,000 CZK to 10,000,000 CZK was used. This value is a constant value and the first simulation is done with 2,000,000 CZK |
Value of Property = 2,000,000 | Value of Property = 2,000,000 | ||
| Line 79: | Line 79: | ||
'''Down Payment''' | '''Down Payment''' | ||
| − | This is the percentage of the value of the property required before loan is given. In the Czech Republic, a down payment of 20% is usually required for mortgages. | + | This is the percentage of the value of the property required before loan is given. In the Czech Republic, a down payment of 20% is usually required for mortgages. |
Down Payment = 0.2 * Value of Property | Down Payment = 0.2 * Value of Property | ||
| Line 85: | Line 85: | ||
'''Life of Loan (Years)''' | '''Life of Loan (Years)''' | ||
| − | This is the total number of years required to repay the entire loan amount. This ranges between 10 to 35 years. The first simulation is done with 30 years | + | This is the total number of years required to repay the entire loan amount. This ranges between 10 to 35 years. The first simulation is done with 30 years |
Life of Loan (Years) = 30 | Life of Loan (Years) = 30 | ||
| Line 91: | Line 91: | ||
'''Repayment Period''' | '''Repayment Period''' | ||
| − | This is the total number of months required to repay the entire loan amount. | + | This is the total number of months required to repay the entire loan amount. |
Repayment Period = "Life of Loan (years)"* 12 | Repayment Period = "Life of Loan (years)"* 12 | ||
| Line 97: | Line 97: | ||
'''Interest Rate''' | '''Interest Rate''' | ||
| − | Mortgage interest rates in the Czech Republic ranges from 6% to 7%. For this model, The first simulation is done with 6.5%. | + | Mortgage interest rates in the Czech Republic ranges from 6% to 7%. For this model, The first simulation is done with 6.5%. |
Interest Rate = 0.065 | Interest Rate = 0.065 | ||
| Line 103: | Line 103: | ||
'''Month Repayment Amount''' | '''Month Repayment Amount''' | ||
| − | This is the monthly repayment amount for the total mortgage. This amount usually has four parts: loan principal, loan interest, taxes, and insurance. | + | This is the monthly repayment amount for the total mortgage. This amount usually has four parts: loan principal, loan interest, taxes, and insurance. |
Month Repayment Amount = (("Principal (Mortgage Loan Amount)" * Interest Rate/12) / 1 - (1 + Interest Rate/12)^(-Repayment Period)) + Tax Per Month + Insurance Per Month | Month Repayment Amount = (("Principal (Mortgage Loan Amount)" * Interest Rate/12) / 1 - (1 + Interest Rate/12)^(-Repayment Period)) + Tax Per Month + Insurance Per Month | ||
| Line 109: | Line 109: | ||
'''Total Repayments''' | '''Total Repayments''' | ||
| − | This is the total monthly repayment at any given period. This can also include additional repayment amounts when a borrower wants to reduce the repayment period. | + | This is the total monthly repayment at any given period. This can also include additional repayment amounts when a borrower wants to reduce the repayment period. |
Total Repayments = ((Monthly Repayment Amount * Period Elapsed) - (Number of Default * Period Elapsed * Monthly Repayment Amount)) + Additional Repayment | Total Repayments = ((Monthly Repayment Amount * Period Elapsed) - (Number of Default * Period Elapsed * Monthly Repayment Amount)) + Additional Repayment | ||
| Line 115: | Line 115: | ||
'''Number of Default''' | '''Number of Default''' | ||
| − | This is when a borrower fails to fulfil repayment obligations. Defaults a due can be due to several conditions such Loss of Employment, Reduction in Income and Ill Health. For this model, we considered the effect of the a number of defaults on repayment time and ability to repay. Also, the max number of loan years is 35 years hence the max default period can be 420 months. The first simulation is done with 0 default. | + | This is when a borrower fails to fulfil repayment obligations. Defaults a due can be due to several conditions such Loss of Employment, Reduction in Income and Ill Health. For this model, we considered the effect of the a number of defaults on repayment time and ability to repay. Also, the max number of loan years is 35 years hence the max default period can be 420 months. The first simulation is done with 0 default. |
Number of Default = 0 | Number of Default = 0 | ||
| Line 121: | Line 121: | ||
'''Total Mortgage''' | '''Total Mortgage''' | ||
| − | This is the total value of the loan when interest is included. | + | This is the total value of the loan when interest is included. |
Total Mortgage = ("Repayment Period (Months)" * Monthly Repayment Amount) | Total Mortgage = ("Repayment Period (Months)" * Monthly Repayment Amount) | ||
| Line 127: | Line 127: | ||
'''Additional Repayment''' | '''Additional Repayment''' | ||
| − | This is any additional repayments the borrower makes outside the monthly repayment amount. For this model, this ranges from )CZK to 1,000,000CZK. The first simulation is done with 0CZK. | + | This is any additional repayments the borrower makes outside the monthly repayment amount. For this model, this ranges from )CZK to 1,000,000CZK. The first simulation is done with 0CZK. |
Additional Repayment = 10000 | Additional Repayment = 10000 | ||
| Line 133: | Line 133: | ||
'''Period Elapsed''' | '''Period Elapsed''' | ||
| − | This is a time period (in months) after loan was secured. The first simulation is done with 1 month after loan was taken. | + | This is a time period (in months) after loan was secured. The first simulation is done with 1 month after loan was taken. |
Period Elapsed = 1 | Period Elapsed = 1 | ||
| Line 139: | Line 139: | ||
'''Total Mortgage Outstanding''' | '''Total Mortgage Outstanding''' | ||
| − | This the Total Mortgage value less Total Repayments made. | + | This the Total Mortgage value less Total Repayments made. |
Total Mortgage Outstanding = Total Mortgage -Total Repayments | Total Mortgage Outstanding = Total Mortgage -Total Repayments | ||
| Line 149: | Line 149: | ||
== How to Use Model == | == How to Use Model == | ||
| − | The key outputs of this model are | + | The key outputs of this model are: |
1. The Monthly Repayment Amount | 1. The Monthly Repayment Amount | ||
| + | |||
2. Total Mortgage Amount | 2. Total Mortgage Amount | ||
| + | |||
3. Total Amount Repaid | 3. Total Amount Repaid | ||
| + | |||
4. Total Mortgage Outstanding | 4. Total Mortgage Outstanding | ||
| + | |||
To simulate these outputs, a user will adjust the variables listed below. The resulting output depends on a combination of these inputs: | To simulate these outputs, a user will adjust the variables listed below. The resulting output depends on a combination of these inputs: | ||
1. Premium Percentage | 1. Premium Percentage | ||
| + | |||
2. Tax Rate | 2. Tax Rate | ||
| + | |||
3. Value of Property | 3. Value of Property | ||
| + | |||
4. Interest Rate | 4. Interest Rate | ||
| + | |||
5. Life of Loan | 5. Life of Loan | ||
| + | |||
6. Number of Defaults | 6. Number of Defaults | ||
| + | |||
7. Additional Repayments | 7. Additional Repayments | ||
| + | |||
8. Period Elapsed | 8. Period Elapsed | ||
| + | |||
The resulting outputs can be analyzed using the following tools available on Vensim: | The resulting outputs can be analyzed using the following tools available on Vensim: | ||
1. Causes Strip | 1. Causes Strip | ||
| + | |||
2. Graph | 2. Graph | ||
| + | |||
3. Table | 3. Table | ||
| + | |||
4. Table Time Down | 4. Table Time Down | ||
| − | |||
== Results == | == Results == | ||
| Line 182: | Line 196: | ||
'''Result One''' | '''Result One''' | ||
| − | Loan life of 30 years, | + | |
| + | Loan life of 30 years, 0 CZK Additional Repayment, 0 CZK Additional Repayments, Repayment Period = 360 months, Period Elapsed = 360 months, No Defaults | ||
[[File:MOrtgages Outstanding 2.png]] | [[File:MOrtgages Outstanding 2.png]] | ||
| − | From this simulation | + | From this simulation, it is clear that when monthly repayments are paid as scheduled with no defaults and no additional repayments, full amount is paid within expected repayment time. |
'''Result Two''' | '''Result Two''' | ||
| − | Loan life of 30 years, 240,000 CZK Additional Repayment, | + | |
| + | Loan life of 30 years, 240,000 CZK Additional Repayment, 0 CZK Additional Repayments, Repayment Period = 360 months, Period Elapsed = 360 months, No Defaults | ||
[[File:MOrtgages Outstanding 3.png]] | [[File:MOrtgages Outstanding 3.png]] | ||
| − | From this simulation | + | From this simulation, it is clear that when monthly repayments are paid as scheduled with no defaults and some additional repayments, full amount is paid ahead of repayment time. This can be shown by the negative graph |
'''Result Three''' | '''Result Three''' | ||
| + | |||
Loan life of 30 years, 240,000 CZK Additional Repayment, O CZK Additional Repayments, Repayment Period = 360 months, Period Elapsed = 360 months, 95 months of Defaults | Loan life of 30 years, 240,000 CZK Additional Repayment, O CZK Additional Repayments, Repayment Period = 360 months, Period Elapsed = 360 months, 95 months of Defaults | ||
[[File:MOrtgages Outstanding 4.png]] | [[File:MOrtgages Outstanding 4.png]] | ||
| − | From this simulation | + | From this simulation, it is clear that when there are defaults, full amount cannot be paid within expected repayment time even with additional repayments. Larger additional repayment amounts might be required to repay on time or ahead of time. |
== Conclusion == | == Conclusion == | ||
| − | From the simulation, we can concluded that several factor contribute to the overall amount owed to a lender. Taxes, Insurance add to Interest to determine amount owed. A borrower must strife to avoid defaults. Defaults extend repayment period and make mortgage more expensive. In situations where defaults are unavoidable, a borrower should plan toward additional repayments. | + | From the simulation, we can concluded that several factor contribute to the overall amount owed to a lender. Taxes, Insurance add to Interest to determine amount owed. A borrower must strife to avoid defaults. Defaults extend repayment period and make mortgage more expensive. In situations where defaults are unavoidable, a borrower should plan toward additional repayments. |
| + | |||
| + | Defaults a due can be due to several conditions such Loss of Employment, Reduction in Income and Ill Health though this was not factored in the calculations. | ||
== References == | == References == | ||
Latest revision as of 22:44, 22 January 2023
Contents
Introduction
A mortgage is a form of loan used to purchase or maintain a home, land, or other type of real estate. The borrower commits to repay the lender over time, often through a series of monthly payments divided into principal and interest repayments. These components are influenced by different factors and elements and for the purpose of this work, only factors relevant to the simulation were selected. Each component and their associated factors will be further explained under the variable section of this work. The monthly mortgage payment is made up of four key components: Principle, Interest, Taxes, and Insurance (PITI). Mortgages in the Czech Republic, like in the rest of the world, typically have a payback duration of 10 to 30 years, however this can be extended.
Borrowers can choose from a variety of mortgage loans, the most common of which are fixed-rate mortgages (FRM) and adjustable-rate mortgages (ARMs).
Fixed-Rate Mortgages A fixed-rate mortgage is the most common form. The interest rate on a fixed-rate mortgage remains constant throughout the loan's duration, as do the borrower's monthly mortgage payments. A conventional mortgage is another name for a fixed-rate mortgage.
Adjustable-Rate Mortgages An adjustable-rate mortgage (ARM) has an interest rate that is fixed for a set length of time before changing based on market interest rates. The initial interest rate is frequently below market, making the mortgage more reasonable in the near term but potentially less affordable in the long run if the rate rises significantly.
This model simulates mortgage repayments based on the principal, interest, tax and insurance. This simulation will show how default, extra payments, and payback duration affect early or late repayment or inability to repay. This study is based on the Fixed-Rate Model and focuses on the mortgage market in the Czech Republic.
Simulation Tool Used
Vensim PLE
Method
The method used involved create a model using real-life mortgage conditions in the Czech Republic and general principle of mortgage calculations. For certain variables, the author assigned values not based on real-world estimates or values.
Variables
Principal (Mortgage Loan Amount)
The principle of your mortgage loan is the amount payable before interest is calculated. This is the property's worth less the down payment.
Principal (Mortgage Loan Amount) = Value of House - Down Payment
Interest
An interest rate is a percentage that indicates how much you will pay your lender as a monthly fee for borrowing money. Interest is calculated by your mortgage lender as a proportion of your principle over time.
Interest = INTEG [(Interest Rate * "Principal (Mortgage Loan Amount)"), 0]
Tax
The amount of property tax you will pay is decided by the state, city, and the value of your home.
Tax = INTEG [(Tax Rate * Value of House), 0]
Insurance
Mortgage insurance protects the lender if a borrower defaults on the loan. For this work, it is approximated using a premium rate and the value of the house. Your credit score is also considered while calculating the premium rate.
Insurance = INTEG [(Premium Percentage * Value of House), 0]
Premium Percentage
The premium percentage used here is based on a borrowers credit scores. Higher credit scores equal lower rate. A range of 10% to 40% was used. This value is a constant value.
Premium Percentage = 0.2
Insurance Per Month
This is the monthly amount of insurance which forms part on monthly loan repayment amount. This is amount collected is collected in escrow accounts and paid to the insurance company periodically.
Insurance Per Month = Insurance/12
Tax Rate
This is the property tax rate of the Czech Republic.
Tax Rate = 0.04
Tax Per Month
This is the monthly amount of tax which forms part on monthly loan repayment amount. This is amount collected is collected in escrow accounts and paid to the government periodically.
Tax Per Month = Tax / 12
Value of Property
The is the price of the property a borrower is taking a loan to purchase. A range of 1,500,000 CZK to 10,000,000 CZK was used. This value is a constant value and the first simulation is done with 2,000,000 CZK
Value of Property = 2,000,000
Down Payment
This is the percentage of the value of the property required before loan is given. In the Czech Republic, a down payment of 20% is usually required for mortgages.
Down Payment = 0.2 * Value of Property
Life of Loan (Years)
This is the total number of years required to repay the entire loan amount. This ranges between 10 to 35 years. The first simulation is done with 30 years
Life of Loan (Years) = 30
Repayment Period
This is the total number of months required to repay the entire loan amount.
Repayment Period = "Life of Loan (years)"* 12
Interest Rate
Mortgage interest rates in the Czech Republic ranges from 6% to 7%. For this model, The first simulation is done with 6.5%.
Interest Rate = 0.065
Month Repayment Amount
This is the monthly repayment amount for the total mortgage. This amount usually has four parts: loan principal, loan interest, taxes, and insurance.
Month Repayment Amount = (("Principal (Mortgage Loan Amount)" * Interest Rate/12) / 1 - (1 + Interest Rate/12)^(-Repayment Period)) + Tax Per Month + Insurance Per Month
Total Repayments
This is the total monthly repayment at any given period. This can also include additional repayment amounts when a borrower wants to reduce the repayment period.
Total Repayments = ((Monthly Repayment Amount * Period Elapsed) - (Number of Default * Period Elapsed * Monthly Repayment Amount)) + Additional Repayment
Number of Default
This is when a borrower fails to fulfil repayment obligations. Defaults a due can be due to several conditions such Loss of Employment, Reduction in Income and Ill Health. For this model, we considered the effect of the a number of defaults on repayment time and ability to repay. Also, the max number of loan years is 35 years hence the max default period can be 420 months. The first simulation is done with 0 default.
Number of Default = 0
Total Mortgage
This is the total value of the loan when interest is included.
Total Mortgage = ("Repayment Period (Months)" * Monthly Repayment Amount)
Additional Repayment
This is any additional repayments the borrower makes outside the monthly repayment amount. For this model, this ranges from )CZK to 1,000,000CZK. The first simulation is done with 0CZK.
Additional Repayment = 10000
Period Elapsed
This is a time period (in months) after loan was secured. The first simulation is done with 1 month after loan was taken.
Period Elapsed = 1
Total Mortgage Outstanding
This the Total Mortgage value less Total Repayments made.
Total Mortgage Outstanding = Total Mortgage -Total Repayments
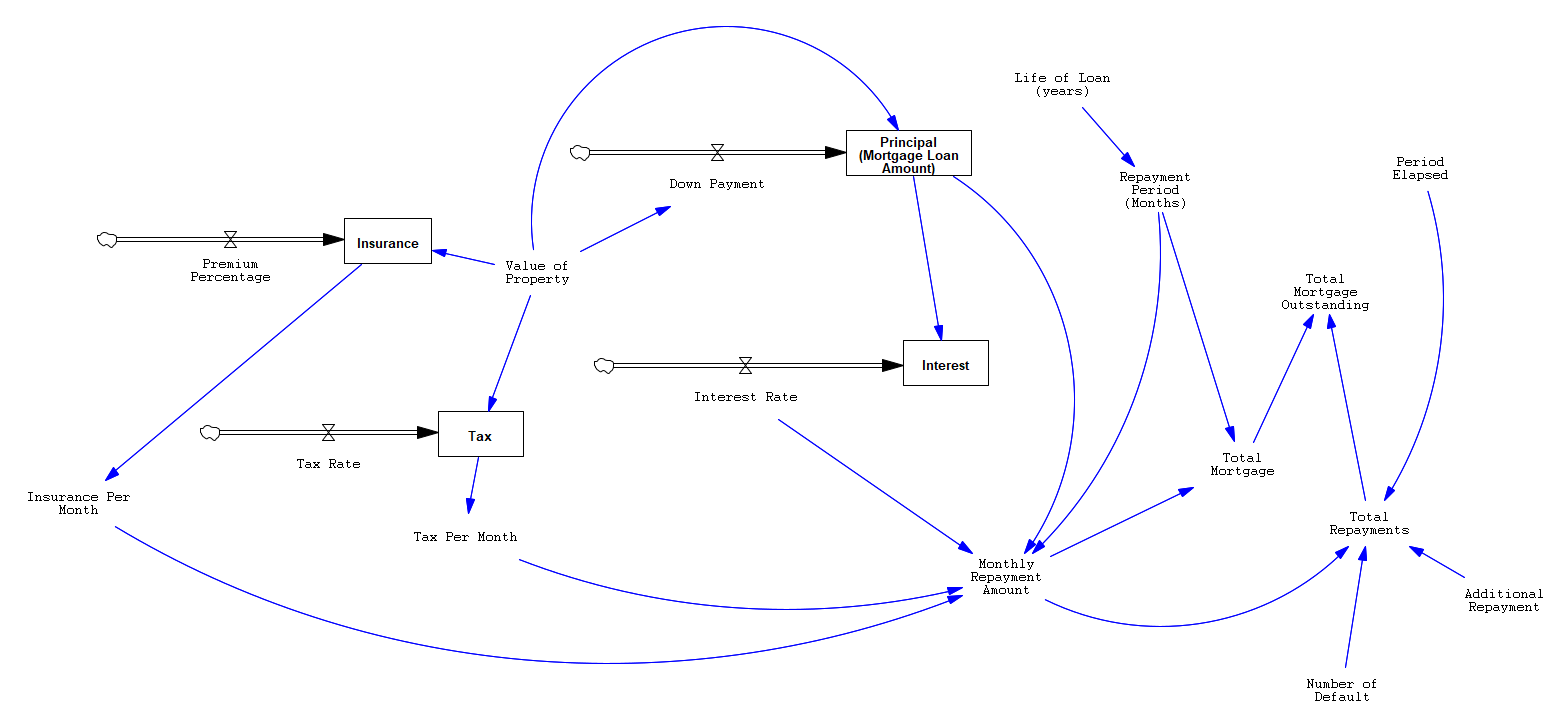
Model
The Stock Flow Diagram construct using the variables discussed is shown below.
How to Use Model
The key outputs of this model are:
1. The Monthly Repayment Amount
2. Total Mortgage Amount
3. Total Amount Repaid
4. Total Mortgage Outstanding
To simulate these outputs, a user will adjust the variables listed below. The resulting output depends on a combination of these inputs:
1. Premium Percentage
2. Tax Rate
3. Value of Property
4. Interest Rate
5. Life of Loan
6. Number of Defaults
7. Additional Repayments
8. Period Elapsed
The resulting outputs can be analyzed using the following tools available on Vensim:
1. Causes Strip
2. Graph
3. Table
4. Table Time Down
Results
The result of this model vary depending of various variable adjustments as discussed under the "How to Use Model" section.
Four graphical results showing Total Mortgage Outstanding are presented below to demonstrate how the model works. The scenario adopted are listed above the graph
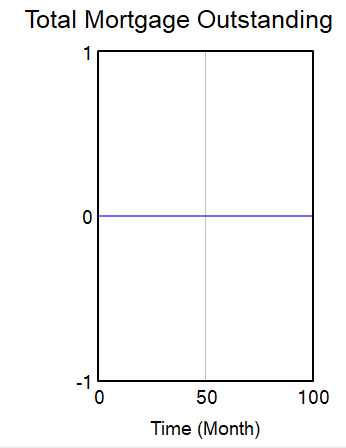
Result One
Loan life of 30 years, 0 CZK Additional Repayment, 0 CZK Additional Repayments, Repayment Period = 360 months, Period Elapsed = 360 months, No Defaults
From this simulation, it is clear that when monthly repayments are paid as scheduled with no defaults and no additional repayments, full amount is paid within expected repayment time.
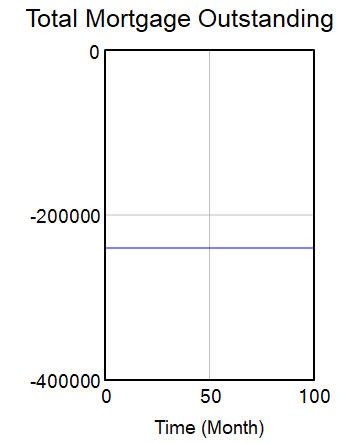
Result Two
Loan life of 30 years, 240,000 CZK Additional Repayment, 0 CZK Additional Repayments, Repayment Period = 360 months, Period Elapsed = 360 months, No Defaults
From this simulation, it is clear that when monthly repayments are paid as scheduled with no defaults and some additional repayments, full amount is paid ahead of repayment time. This can be shown by the negative graph
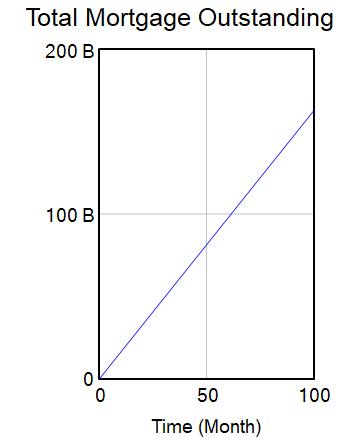
Result Three
Loan life of 30 years, 240,000 CZK Additional Repayment, O CZK Additional Repayments, Repayment Period = 360 months, Period Elapsed = 360 months, 95 months of Defaults
From this simulation, it is clear that when there are defaults, full amount cannot be paid within expected repayment time even with additional repayments. Larger additional repayment amounts might be required to repay on time or ahead of time.
Conclusion
From the simulation, we can concluded that several factor contribute to the overall amount owed to a lender. Taxes, Insurance add to Interest to determine amount owed. A borrower must strife to avoid defaults. Defaults extend repayment period and make mortgage more expensive. In situations where defaults are unavoidable, a borrower should plan toward additional repayments.
Defaults a due can be due to several conditions such Loss of Employment, Reduction in Income and Ill Health though this was not factored in the calculations.
References
Madison , L.F. (2019) Understanding the four parts of a mortgage payment, NCHFA. Available at: https://www.nchfa.com/news/home-matters-blog/understanding-four-parts-mortgage-payment (Accessed: January 18, 2023).
Shea, N. (2017) Seven factors that determine your mortgage interest rate, Consumer Financial Protection Bureau. Available at: https://www.consumerfinance.gov/about-us/blog/7-factors-determine-your-mortgage-interest-rate/ (Accessed: January 18, 2023).
Analyst Prep (2021) Determinants of interest rates, CFA, FRM, and Actuarial Exams Study Notes. Available at: https://analystprep.com/study-notes/actuarial-exams/soa/fm-financial-mathematics/determinants-of-interest-rates/ (Accessed: January 16, 2023).
Bieber, C. (2021) 5 factors that affect your mortgage rate, The Motley Fool. Available at: https://www.fool.com/the-ascent/mortgages/articles/5-factors-that-affect-your-mortgage-rate/ (Accessed: January 18, 2023).
Crace, M. (no date) What is a mortgage? the basics for beginners, What Is A Mortgage And How Do I Get One? | Rocket Mortgage. Available at: https://www.rocketmortgage.com/learn/what-is-a-mortgage#:~:text=A%20mortgage%20is%20a%20type,the%20collateral%20is%20the%20home. (Accessed: January 16, 2023).
Kagan, J. (2023) What is a mortgage? types, how they work, and examples, Investopedia. Investopedia. Available at: https://www.investopedia.com/terms/m/mortgage.asp (Accessed: January 17, 2023).
NerdWallet (no date) PMI Calculator, NerdWallet. Available at: https://www.nerdwallet.com/article/mortgages/pmi-calculator (Accessed: January 16, 2023).
Pexpats (no date) How to get a mortgage in the Czech Republic as a foreigner. Available at: https://pexpats.com/how-to-get-a-czech-mortgage (Accessed: January 15, 2023).