Difference between revisions of "Prisoner's dilemma"
(→Prisoner’s dilemma in Eurozone) |
m (the cited webpage has moved) |
||
| (6 intermediate revisions by one other user not shown) | |||
| Line 147: | Line 147: | ||
Finally, more interactive example of prisoner’s dilemma in real life is a British game show '''[http://www.goldenballstvshow.com/ “Golden Balls”]'''. You can can check it out on YouTube, but let us take a look at the rules. There are two players, who play a game very similar to out prisoner’s dilemma and the prize is 100,000 pounds. Each of the players can choose either to split or steal. If both players split, then each one gets 50,000 pounds. If one player splits and the other steals, the person who split gets 100,000 and the other person gets 0. And finally, if both of them steal, then they both get 0. But the main difference is that before they start making their decisions, playes can talk for a few minutes and presumably convince the other person that they plan to split. Try to watch couple of episodes of this game and understand, what will be the best strategy to win. Then imagine that you play with a total stranger and then with someone you know. And then that you play one time or there are more games in one set [http://gametheoryinpractice.blogspot.com/2009/08/split-or-steal.html]. | Finally, more interactive example of prisoner’s dilemma in real life is a British game show '''[http://www.goldenballstvshow.com/ “Golden Balls”]'''. You can can check it out on YouTube, but let us take a look at the rules. There are two players, who play a game very similar to out prisoner’s dilemma and the prize is 100,000 pounds. Each of the players can choose either to split or steal. If both players split, then each one gets 50,000 pounds. If one player splits and the other steals, the person who split gets 100,000 and the other person gets 0. And finally, if both of them steal, then they both get 0. But the main difference is that before they start making their decisions, playes can talk for a few minutes and presumably convince the other person that they plan to split. Try to watch couple of episodes of this game and understand, what will be the best strategy to win. Then imagine that you play with a total stranger and then with someone you know. And then that you play one time or there are more games in one set [http://gametheoryinpractice.blogspot.com/2009/08/split-or-steal.html]. | ||
| − | You can also try out an online version of this model | + | You can also try out an online version of this model to better understand the whole concept '''[http://serendip.brynmawr.edu/bb/pd.html Serendip’s Exchange: You Have Found The Prisoners’ Dilemma]'''. |
Hopefully, the problematic of this model is now more clear to you and you can use it not only in theory, but also to solve real problems and tasks. Good luck! | Hopefully, the problematic of this model is now more clear to you and you can use it not only in theory, but also to solve real problems and tasks. Good luck! | ||
| Line 203: | Line 203: | ||
11. WAYNE, Davis. PRISONER’S DILEMMA [online]. March 22nd, 2007 [cit. 2012-04-10]. | 11. WAYNE, Davis. PRISONER’S DILEMMA [online]. March 22nd, 2007 [cit. 2012-04-10]. | ||
| − | Available from: http://www.iterated-prisoners-dilemma. | + | Available from: http://www.iterated-prisoners-dilemma.info/ |
| + | |||
| + | =References= | ||
| + | |||
| + | 1. http://plato.stanford.edu/entries/game-theory/ | ||
| + | |||
| + | 2. http://plato.stanford.edu/entries/game-theory/#Games | ||
| + | |||
| + | 3. http://plato.stanford.edu/entries/game-theory/#Util | ||
| + | |||
| + | 4. http://www.informs.org/About-INFORMS/History-and-Traditions/Miser-Harris-Presidential-Portrait-Gallery/Merrill-M.-Flood | ||
| + | |||
| + | 5. http://www.rand.org/pubs/authors/d/dresher_melvin.html | ||
| + | |||
| + | 6. http://www.rand.org/about.html | ||
| + | |||
| + | 7. http://www.nytimes.com/1995/01/27/obituaries/albert-w-tucker-89-pioneering-mathematician.html | ||
| + | |||
| + | 8. http://www-cs-faculty.stanford.edu/~eroberts/courses/soco/projects/1998-99/game-theory/nonzero.html | ||
| + | |||
| + | 9. http://www.press.umich.edu/titleDetailLookInside.do?id=20269 | ||
| + | |||
| + | 10. http://www.apn.ru/publications/article19740.htm | ||
| + | |||
| + | 11. http://tuvalu.santafe.edu/~jkchoi/game4.pdf | ||
| + | |||
| + | 12. http://shporiforall.ru/shpory/ek-teorii/2-dilemma-zaklyuchennogo-matrica-vyigrysha-ravnovesie-nesha-dominiruyushhaya-strategiya.html | ||
| + | |||
| + | 13. http://www.iterated-prisoners-dilemma.info/ | ||
| + | |||
| + | 14. http://plato.stanford.edu/entries/prisoner-dilemma/ | ||
| + | |||
| + | 15. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.176.6993 | ||
| + | |||
| + | 16. http://bizkiev.com/content/view/822/205/ | ||
| + | |||
| + | 17. http://www.goldenballstvshow.com/ | ||
| + | |||
| + | 18. http://serendip.brynmawr.edu/bb/pd.html | ||
| + | |||
| + | =Additional files= | ||
| + | |||
| + | [[media:Prisoner_dilemma_eng.pdf|Prisoner's Dilemma chapter]] | ||
Latest revision as of 02:14, 18 October 2020
Contents
Introduction
In this chapter we will try to explain the essence of such problem as “prisoner’s dilemma”. For a start, let’s have a look at the definition of this concept that classical science presents.
PRISONER’S DILEMMA is a fundamental problem in game theory, under which players will not always cooperate with each other, even if it is in their interest. The theoretical idea which is reflected in this model sounds like this – self-interest may interfere with the achievement of the collective goal. This collective goal is considered to be of his own interests by each individual included into this game. This model is being widely used in many modern works on the theory of ethics and social theory, mainly in the consideration of situations with a contradiction between individual and common interests. But for the start we will consider this dilemma in terms of game theory. This model also assumes that the player (“prisoner”) maximizes his own gain, without caring about the benefit of others. We will also take a look at the variant with altruistic players later in this chapter. [1]
Let’s see who the players are and what the game itself in this case is. The game refers to the process, which involves two or more parties fighting for the their interests. Each party has its own goal and uses some strategy that can lead to a gain or loss - depending on the behavior of other players. Accordingly, players are some rational individuals who have an interest in the outcome of the game and opportunities to influence it. Simply put, players can play. Rationality of a player in this definition means that he has a coherent system of preferences in the outcome of the game and it is constant during the whole game. He chooses his actions in order to achieve the best outrome from the standpoint of the system, and for that he is using all the information at his disposal. Simply put, a player wants to win. Or, if it is not possible to win, to at least minimize his loss (which also means winning in some way).
Prisoner’s dilemma – who is who?
Now that we understand the basic concepts, let us return to the prisoner’s dilemma itself. A quick historical note, just for your information. The essence of the problem was formulated by two american mathematicians, not prosecutors and investigators – Merrill Flood and Melvin Dresher in 1950. They formulated this dilemma and it was used by RAND Corporation in the development strategies of nuclear confrontation. The name of the dilemma was given by american mathematician Albert Tucker.
Betrayal strictly dominates cooperation in the prisoner’s dilemma, so the only possible equilibrium is a betrayal of both players. Simply put, no matter what the other player will do, everyone will benefit more of betrayal. Because in any situation betraying is more profitable than cooperation, all rational players will choose first variant.
Behaving rationally individually, together participants will come to a waste solution: if both betray each other, in total they will receive a smaller gain than if they had cooperated. Here lies the dilemma. In other words, this concept shows us how it is more profitable to achieve the mutually obligatory agreement.
Formal definition of the prisoner’s dilemma
PRISONER’S DILEMMA is best known example of a nonzero-sum game where the «best» decision remains ambivalent. The theory of a nonzero-sum games distinguishes between cooperative and noncooperative games. In a cooperative game, players can make agreements to choose strategies jointly. In noncooperative games they cannot do so.
PRISONER’S DILEMMA is, by definition, a noncooperative game. If it were a cooperative game, the dilemma, it is argued, would disappear, because then the prisoners could make a pact not to confess, a pack from which each would derive a benefit.
It is clear, however, that if the pact is not enforceable, a new dilemma arises. For now each of the prisoners faces a decision of keeping the pact or breaking it. This choice induces another game exactly like prisoner’s dilemma, because it is in the interest of each to break the pact regardless of whether the other keeps it.
In this game the rational choice of strategy by both players leads to an outcome which is worse for both players than if they had chosen their strategies "irrationally". The paradox remains unresolved as long as we insist on adhering to the concept of rationaloty which makes perfect sense in zero-sum games but which makes questionable sense in nonzero-sum games. Thus the paradox forces a reexamination of our concept of rational decision. Herein lies a potential contribution by game theory to psychology and to behavioral science in general. [2]
Basic concept
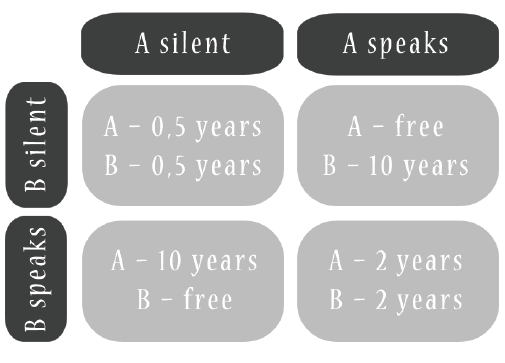
Let us now take a look at the classical concept of the prisoner’s dilemma. The legend says that once upon a time there were two criminals, Alfred (A) and Benjamin (B), who were caught for stealing two cars. They stole it separately from each other, but police suspected that our A and B acted together, as a band. This was only a speculation, sadly police had no evidence.
Police offered a deal to each one of the criminals: tell the truth about his companion and buy himself a freedom, while his companion will be sentenced to 10 years of prison. If the criminal refuses to testify, he gets 6 months in jail for refusing to cooperate with the investigation. If both testify against each other, both get 2 years in prison.
Criminals are isolated from each other and can not communicate. Their main interest is to reduce their own stay in jail as much as possible. What decision should take each of them: to make a deal with the investigation or to remain silent? Before you look for a solution in this chapter, try to imagine yourself in situation like this and decide what you would do and why? And then try to compare your answer with what science think of it:)
Unable to communicate with each other, criminals have to give each other away. After all, in fact, there are only four possible options:
If suspects are not allowed to talk, they do not know what the other one will do. In this situation, if A remains silent, he is dependent on B’s desicion and will ether sentenced for 10 years or 6 months. If A will testify against B, then as a result A will get 2 years in prison or will be released [3].
Thus, it would be better for each of the suspects to testify against each other, so that they will not to be condemned for 10 years. But if A and B have had the opportunity to communicate, then, of course, the best solution for each of them would be not make a deal with the investigation and get only 6 months in prison. This little problem illustrates that sometimes, acting solely in your personal interests will not always lead to the best results for others and for yourself. By acting for themselves, both prisoners went to jail for 2 years, when in fact they could do with only a half-year of imprisonment.
Game balance
Each prisoner can accurately predict his win in each of the four situations. As you know, the balance of the game in game theory is Nash equilibrium. The prisoner’s dilemma is a game with a special kind of Nash equilibrium – dominant strategy equilibrium. But before we get to the dominant strategy equilibrium, let’s briefly review what is a normal Nash equilibrium.
NASH EQUILIBRIUM is the type of game solution of 2 or more players, in which neither party can increase their gain by changing his decision unilaterally while other members do not change their decisions. Accordingly, such a set of strategies chosen by participants and their winnings is called a Nash equilibrium. In other words, everything depends not only on you. [4]
But let us return to our problem. So, we still have 2 prisoners, sitting in 2 different cells without the possibility to agree on what to do next. And there are 4 possible variants of the outcome. Remember, you had put yourself in the shoes of one of them? Let us repeat the experience, and thinking only rationally, try to make a decision. If we are afraid, we are more likely to think only about ourselves. Fear switches on instinct of self-preservation which is often stronger than moral standards and obligations.
Here is an estimated stream of thoughts in this case: “If I, Alfred, will remain silent, but Benjamin will tell them everything, then I am going to jail for 10 years. This simply can not happen. If I will tell them everything and he will do so as well, then we both stuck in here for 2 years. Too bad, but still it is better then 10 years. If Benji will remain silent, and I will tell the truth to the police, then he will stay here for 10 years, but I will be free (although I will probably suffer from insomnia caused by my dishonesty). Of course, there is a chance that he will not speak, and if I will do the same, then we both will get only half a year in jail. But again, the risk of getting 10 years in prison is to high. So, I will not keep my mouth shut and will give testimonies on him. It does not matter if he will or will not speak, I will avoid the worst – ten years in prison, and maybe I will even go home tomorrow, if he will be quiet.“
Acting rationally in their own interest, the participants of this game come to an irrational result: in any case, both will get in jail, the only question is – for how long; but they could get a relatively short imprisonment if they were convinced that the other one will not say anything. The dilemma of “keeping silence – testifying” is resolved in favor of testimony, although in terms of the collective interest this decision, to put it mildly, is not optimal.
Now let us mentally put ourselves in the policeman shoes. His goal is to knock out the testimony. He can not change human characteristics of suspects, but he can put them in a context in which they will behave in a predictable manner. There are only two leverages in the hands of the police: fear and isolation. And they are more than enough to force the prisoners to act in police interests, rather than their own.
Extensions of normal model
Iterated prisoner’s dilemma
Scenario goes like this: you and your colleague, Lucifer, are in jail and suspected of committing a crime. You are isolated from each other and do not know how the other will respond to questioning. The police invite both of you to implicate the other in the crime (defect). What happens depends on what both of you do, but neither of you know how the other will respond. If Lucifer betrays you (yields to the temptation to defect) while you remain silent, then you receive the longest jail term while Lucifer gets off free (and visa versa). If you both choose to cooperate with each other (not the police) by remaining silent, there is insufficient evidence to convict both of you, so you are both given a light sentence for a lesser crime. If both of you decide to defect, then you have condemned each other to slightly reduced but still heavy sentences.
The payoff in this game is a reduction in prison sentencing of very good, fairly good, fairly bad or very bad, which is translated into a point score system as is shown at the scheme. [5]
Finite Iteration
Many of the situations that are alleged to have the structure of the PD, like defense appropriations of military rivals or price setting for duopolistic firms are better modeled by an iterated version of the game in which players play the PD repeatedly, retaining access at each round to the results of all previous rounds. In these iterated PDs players who defect in one round can be “punished” by defections in subsequent rounds and those who cooperate can be rewarded by cooperation. Thus the appropriate strategy for rationally self-interested players is no longer obvious. The theoretical answer to this question, it turns out, depends strongly on the definition of IPD employed and the knowledge attributed to rational players.
An IPD can be represented in extensive form by a tree diagram like one you can see at the scheme.
There is a significant theoretical difference on this matter between IPDs of fixed, finite length, like the one pictured above, and those of infinite or indefinitely finite length. In practice, there is not a great difference between how people behave in long fixed-length IPDs (except in the final few rounds) and those of indeterminate length. [6]
The Centipede and the Finite IPD
Many of the issues raised by the fixed-length IPD can be raised in even starker form by a somewhat simpler game. Consider a PD in which they punishment payoff is zero. Now iterate the asynchronous version of this game a fixed number times. Imagine that both players are restricted to highly “punitive” strategies according to which, they must always defect against a player who has ever defected. The result is a centipede game.
A stack of N one-dollar bills lies on a table. Players take turns taking money from the stack, one or two bills per turn. The game ends when the stack runs out or one of the players takes two bills (whichever comes first). Both players keep what they have taken to that point. The extensive form of the game with N=4 can be seen at the picture.
The centipede mainly raises the questions about cooperation and socially desirable altruism as does the PD and it is a favorite tool in empirical investigations of game playing [7]
Infinite Iteration
One way to avoid the dubious conclusion of the backward induction argument without delving too deeply into conditions of knowledge and rationality is to consider infinitely repeated PDs. No human agents can actually play an infinitely repeated game, of course, but the infinite IPD has been considered an appropriate way to model a series of interactions in which the participants never have reason to think the current interaction is their last. In this setting a pair of strategies determines an infinite path through of the game tree. If the payoffs of the one-shot game are positive, their total along any such path is infinite. This makes it somewhat awkward to compare strategies. If we confine ourselves to those strategies that can be implemented by mechanical devices (with finite memories and speeds of computation), however, it turns out that the sequence of payoffs to each player will always, after a finite number of rounds, cycle repeatedly through a particular finite sequence of payoffs. The relative value of such infinite sequences of payoffs can then be identified with the average value of the payoffs in one cycle. This value reflects the limit of average payoff per round as the number of rounds increases. Since there is no last round, it is obvious that backward induction does not apply to the infinite IPD. [8]
N-player Prisoner’s Dilemma
In the N-player prisoner’s dilemma multiple agents (N ≥ 2) interact within their designated group and must choose to cooperate or defect. Any benefit or payoff is received by all participants; any cost is borne by the cooperators only. Hardin describes the N-player prisoner’s dilemma as a «tragedy of the commons» game in which the players are worse off acting according to their self interests than if they were cooperating and coordinating their actions. [9]
Other conditions
Not let us draw out attention to the boundary condition of the prisoner’s dilemma, namely the prison walls, the bars on the windows and a doors with a peepholes. All this indicates, that a person is in trouble already and even if he stands before the choice, the only thing he can do is to continue to lose. The only thing that remains to him is to minimize the inevitable losses.
The strategy of “testifying” strictly dominates over the strategy of “silence”. Similarly, another prisoner will come to the same conclusion. It is evident, that common interest of both prisoners is to work together, to keep silent and get only half of the year in jail. But prisoners are not able to cooperate in taking decisions. In other words, they do not have the opportunity to jointly implement their common interest. So each one of them begins to assert his personal interest, which does not lead to the best result.
But imagine that prisoners have the opportunity to discuss this situation. About what would they want to negotiate? Of course about common silence; as we see from the scheme above – it is the most painless variant for both of them as a group. However, each prisoner, after making sure that the other is convinced of the necessity and reasonableness of making a confession, will not confess himself, because he wants to be released. The fact that each of the prisoners, realizing how coordination of their tactics is mutually beneficial, will be in a better position while playing for himself. In that case he will be released.
As the analysis of options shows, the prisoners can not cooperate, because each of them has a personal interest. It is assumed that in this dilemma each of the prisoners acts according to the number of years he will be held in prison. But let’s imagine that our criminals are not selfish but altruistic, and each one also takes others’ interests into consideration. Then confession of the crime is the neccesary dominant strategy.
This dilemma represents a certain type of situations in which:
- there is a need to make an individual decision on the strategy of behavior in the context of common activity
- a separate participant of this situation is interested in the pursuit of general interest only when this general interest is being pursued by all participants
- because individual interests of participants in this situation as objectively separated individuals are different, in case of ignorance about the intentions of the other participant, each of them is forced to trying to achieve his private interest.
Real life examples
Now that we had more or less figured out what exactly the prisoner’s dilemma is, let’s see where in real life it is being used and how it helps to solve real-life conflict situations. Among the reasons of enormous popularity of prisoner’s dilemma let’s allocate one: it describes the choice that confronts us every day throughout our lives. It’s a choice between solidarity with other people and ou personal interests.
Many situations in the society are characterized by similar divergence between the decisions dictated by the individual and collective rationality. Famous examples are price wars and the arms race. In the context of the “prisoner’s dilemma” rejection should be considered as a cooperative strategy (of course with a partner and not with the authorities), and confession – non-cooperative or “cheating.”
Prisoner’s dilemma in Eurozone
Current situation with investors who run away from Greece illustrates the dilemma very well. In economic theory this is called a “coordination trap” or inefficient stable equilibrium. It is the same balance as in our dilemma the silence and cooperation among the prisoners.
Exactly the same happenes in the eurozone. The tragedy of the situation in which Greece has a huge burden of debt in the absence of adequate tax revenues due to economic crisis, makes the market “pledge to each other”. Noone believes in a “happy-end” and if you are too slow to react and lay someone down, then you will be layed down yourself. Default seems imminent, and investors want to get rid of the Greek bonds, while their price has not dropped completely, or, even worse, they all turned out to be worthless. Naturally, the new loan that Greece needs so desperately, can be forgetten.
The darkest result of all this might be the country default and rapid erosion of capital in European banks. This will lead to ceasing of lending and the subsequent closing of credit lines in U.S. banks. It will all be accompanied by a collapse in energy prices and the actual stopping of the world economy, as it happened in 2008.
There is an exit out of this situation – only a consistent and aggressive actions of central banks and governments of all countries that could convince investors on the market that the “laying each other down” is not necessary: there will be no default. In fact, this is our situation with the silent prisoners.
Prisoner’s dilemma in price formation proces
There are also many situations in pricing, when in process of creating price a certain group of companies face the prisoner’s dilemma. Often, one company may perceive the possibility of increasing their profits by reducing price for their goods or services. It does price lowering without paying attention to the pricing of its competitors. Simultaneously, its competitors can come to the same conclusioncan. Which means they really could make more money by cutting prices, not minding the actions of the first company. However, if the company and its competitors cut prices – that is, if all parties act in accordance with their own interests unilaterally – in many cases they all may come to a disadvantage in the end. The task of the industry in such situations is to keep prices high, despite the fact that each company would get some benefits from price reduction [10].
Authority and prisoner’s dilemma
Finally, let’s take a look at an example of prisoner’s dilemma within the confines of an authoritarian society. It is enough to imagine any community under the rule of the authoritarian regime. It can be an Arab Spring or post-Soviet society. Since the Arab Spring happened recently, we can not analyze these events properly yet.That is why let’s try to understand what exactly happened after the collapse of the Soviet Union. Fear of approaching poverty and hunger, multiplied by the isolation caused by the destruction of the usual rules of social life and lack of time, immediately gave the results. Multi-million society, which lived in the Soviet solidarity just yesterday, made fast transition to the state of hyper-individualism – unfortunately, such is the power of fear.
In a society, which is built on fear of losing what you have, solidarity in most cases is impossible. The very formulation of the problem as minimizing the loss shapes events in a very certain way. The condition of minimization of losses and the role of a police officer are not discussed in the theoretical model of the prisoner’s dilemma. However, they are the most important feature of the prisoner’s dilemma in its application to real life. So, this game describes the condition of any human cooperation and solidarity. We call this condition: co-operation and solidarity should bring benefits to every member of the group, in which it occurs.
Probably it is not even worth writing about how effectively the model drives society into primitivism and regression. Finally, a few words about how choices in life expand, once you start to look at other people not only in the framework of prisoner’s dilemma, but also considering the option of group redistribution. A person, who sees the world in the light of group redistribution conquers fear. Hypothetical policeman no longer has control over him, because a prisoner is not alone – whole group covers his back. His power increases in proportion to the size and cohesion of this group. In addition, he starts to feel the taste of life, because now he can not only lose, but also win.
Conclusion
Game theory in games
Finally, more interactive example of prisoner’s dilemma in real life is a British game show “Golden Balls”. You can can check it out on YouTube, but let us take a look at the rules. There are two players, who play a game very similar to out prisoner’s dilemma and the prize is 100,000 pounds. Each of the players can choose either to split or steal. If both players split, then each one gets 50,000 pounds. If one player splits and the other steals, the person who split gets 100,000 and the other person gets 0. And finally, if both of them steal, then they both get 0. But the main difference is that before they start making their decisions, playes can talk for a few minutes and presumably convince the other person that they plan to split. Try to watch couple of episodes of this game and understand, what will be the best strategy to win. Then imagine that you play with a total stranger and then with someone you know. And then that you play one time or there are more games in one set [11].
You can also try out an online version of this model to better understand the whole concept Serendip’s Exchange: You Have Found The Prisoners’ Dilemma.
Hopefully, the problematic of this model is now more clear to you and you can use it not only in theory, but also to solve real problems and tasks. Good luck!
Exercises
To be sure that you understood this chapter, try to figure out solutions for following examples.
1. “Perestroika anecdote”
There used to be a so-called story during Perestroika years. Two businessmen agreed, that one will sell another a truck full of tomatoes. They sign a contract. And only after that the first one goes to look for tomatoes, and the second one – for money.
As you can see, it is a classic example of the prisoner’s dilemma. The agreement was signed, but what if the first will find the tomatoes and the other one will not find the money or vice versa? Try to answer following questions:
- Should you trust your business partner in situation like this?
- How far should your trust go?
- Would it be better for non-tomato businessman to stop looking for money, let that simpleton be with his tomatoes. But what reputation will it bring, will there be anyone willing to deal with him in the future?
2. “TV Arms Race“
Two large competiting companies need to determine their budgets on TV advertising for next year. As you can imagine, TV advertising is a very expensive toy. Therefore: more advertising –> lower the income –> lower the quality of goods (for ex., they will save money on the product formula). But if a competitor will give a lot more advertising than they are, they will lose bigger share of their business. Therefore, both companies have the exact same fear – another one will spend hundreds of millions of dollars per year on advertising.
TIP: As a result, advertising race leads to the fact, that no washing powder washes anymore, soda is impossible to drink and at the end of the year companies are hardly above zero.
Sources
1. PRISONER’S DILEMMA. Kafedra jetiki filosofskogo fakul’teta MGU [online]. [cit. 2012-01-19]. Available from: http://www.ethicscenter.ru/en/content/16.htm
2. RAPOPORT, Anatol and Albert M. CHAMMAH. Prisoner’s Dilemma. Michigan: The University of Michigan , Ann Arbor Paperbacks, 2008. ISBN 0-472-06165-8. Available from: http://www.press.umich.edu/titleDetailLookInside.do?id=20269
3. KRYLOV, Dmitrij. Katalazhka i restoran: kak vyrvat’sja iz dilemmy zakljuchjonnogo: Kak perestat’ byt’ pyl’ju.APN – Agenstvo politicheskih novostej [online]. [cit. 2012-01-19]. Available from: http://www.apn.ru/publications/article19740.htm
4. D. REIBSTEIN, David. Cenoobrazovanie: dilemma zakljuchennogo. BIZKIEV – biznes zhurnal [online]. [cit. 2012-01-19]. Available from: http://bizkiev.com/content/view/822/205/
5. «Dilemma zakljuchennogo»: Matrica vyigrysha. Ravnovesie Njesha. Dominirujuwaja strategija. [online]. [cit. 2012-01-19]. Available from: http://shporiforall.ru/shpory/ek-teorii/2-dilemma-zaklyuchennogo-matrica-vyigrysha-ravnovesie-nesha-dominiruyushhaya-strategiya.html
6. T., Sam. Split Or Steal. GAME THEORY IN PRACTICE [online]. 21.08.2009 [cit. 2012-01-22]. Available from: http://gametheoryinpractice.blogspot.com/2009/08/split-or-steal.html
7. http://dic.academic.ru/dic.nsf/econ_dict/20858. Jekonomika. Tolkovyj slovar’. — M.: “INFRA-M”, Izdatel’stvo “Ves’ Mir”. Dzh. Bljek. Obwaja redakcija: d.je.n. Osadchaja I.M.. 2000.
8. Serendip’s Exchange: You Have Found The Prisoners’ Dilemma. Serendip’s Exchange [online]. Wednesday, 08-Jun-2005 12:47:31 EDT [cit. 2012-04-07]. Available from: http://serendip.brynmawr.edu/bb/pd.html
9. REZAEI, Golriz, Michael KIRLEY a Jens PFAU. Evolving Cooperation in the N-player Prisoner’s Dilemma: A Social Network Model. Department of Computer Science and Software Engineering The University of Melbourne, Australia, 2010. Available from: http://jp.poerf.de/papers/Rezaei09evolvingcooperation.pdf. Annual paper. The University of Melbourne, Australia.
10. KUHN, Steven. Stanford Encyclopedia of Philosophy: Prisoner’s Dilemma. Stanford Encyclopedia of Philosophy [online]. Sep 4, 1997, Mon Oct 22, 2007 [cit. 2012-04-07]. Available from: http://plato.stanford.edu/entries/prisoner-dilemma/
11. WAYNE, Davis. PRISONER’S DILEMMA [online]. March 22nd, 2007 [cit. 2012-04-10]. Available from: http://www.iterated-prisoners-dilemma.info/
References
1. http://plato.stanford.edu/entries/game-theory/
2. http://plato.stanford.edu/entries/game-theory/#Games
3. http://plato.stanford.edu/entries/game-theory/#Util
5. http://www.rand.org/pubs/authors/d/dresher_melvin.html
6. http://www.rand.org/about.html
7. http://www.nytimes.com/1995/01/27/obituaries/albert-w-tucker-89-pioneering-mathematician.html
8. http://www-cs-faculty.stanford.edu/~eroberts/courses/soco/projects/1998-99/game-theory/nonzero.html
9. http://www.press.umich.edu/titleDetailLookInside.do?id=20269
10. http://www.apn.ru/publications/article19740.htm
11. http://tuvalu.santafe.edu/~jkchoi/game4.pdf
13. http://www.iterated-prisoners-dilemma.info/
14. http://plato.stanford.edu/entries/prisoner-dilemma/
15. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.176.6993
16. http://bizkiev.com/content/view/822/205/
17. http://www.goldenballstvshow.com/
18. http://serendip.brynmawr.edu/bb/pd.html